
- •Функция
- •Словарные функции
- •Вычислимые функции и машина Тьюринга
- •Словарное представление машины Тьюринга
- •Массовые алгоритмические проблемы
- •Проблема остановки
- •Проблемы пустой ленты и метод сведения
- •Проблема зацикливания.
- •Введение в теорию np-полных задач Задачи, алгоритмы и сложность
- •Задачи, труднорешаемость которых доказуема
- •Np – полные задачи
- •Задачи разновидности языка и кодирование
- •Примеры массовых задач пример 1.”Изоморфизм подграфу”
- •Лекция 4
- •Основы математической логики
- •Бинарная операция импликация:
- •Техника доказательств:
- •Алгебра логики. Логические операции и операции на множествах
- •Стандартные формулы преобразования булевых функций
- •Геометрическая интерпретация
- •Построение простых импликантов
Техника доказательств:
f:RR f(x)=2x
ПРИМЕР 1
Доказать, что х,уR f(x+y)=f(x)+f(y)
Доказательство: возьмем любые два вещественных числа х и у, тогда
 f(x+y)=f(x)+f(y)
f(x+y)=f(x)+f(y)
ПРИМЕР 2
Доказать единственность нейтрального элемента в группе А по умножению (А*х). Предположим, что имеется два различных нейтральных элемента, левосторонний e и правосторонний e’, т.е. :
х ех=х (1)
х xе’=х (2)
Поскольку формула (1) справедлива для любого х, то возьмём в качестве х значение е’ (х=е’), получим ее’=е’. Поскольку формула (2) справедлива для любого х, то возьмём х равный е, получим ее’=е

Теорема.
Существуют два иррациональных числа а и в, такие что ав является рациональным числом.
Доказательство.
а= в=
в= с=
с= –
может быть либо рациональным, либо
иррациональным. Если с – рационально,
то теорема доказана. Если с– иррационально,
то возьмём в качестве а=
–
может быть либо рациональным, либо
иррациональным. Если с – рационально,
то теорема доказана. Если с– иррационально,
то возьмём в качестве а= ,
в=
,
в= ,
когда ав=
,
когда ав= .
Теорема доказана.
.
Теорема доказана.
Алгебра логики. Логические операции и операции на множествах
Определение:
Одноместным предикатом на множестве А называется функция, принимающая на этом множестве 2 значения: 0 и 1.
Пусть
 - некоторое
подмножество множества А. Определим
функцию
- некоторое
подмножество множества А. Определим
функцию

 следующим
образом:
следующим
образом: Данный предикат называется характеристической
функцией множества Х.
Данный предикат называется характеристической
функцией множества Х.
Пусть
Р(А)– множество всех подмножеств
множества А,
 –
множество всех отображений из А в В.
–
множество всех отображений из А в В.
Теорема.
Отображение
множества
 ,
построено следующим образом:
,
построено следующим образом:

 –биективное
отображение
–биективное
отображение

 .
.
Доказательство.
Построим
обратное отображение. Пусть
 -
некоторый предикат из
-
некоторый предикат из .
Положим
.
Положим т.е.
т.е. ,т.е.
мы задали отображение
,т.е.
мы задали отображение .
Покажем, что данное отображение
.
Покажем, что данное отображение обратно отображению, сформулированному
в условии теоремы. Для этого необходимо
показать, что:
обратно отображению, сформулированному
в условии теоремы. Для этого необходимо
показать, что:
1) ;
;
2) ,
, .
.
1)
 –
по определению характеристической
функции.
–
по определению характеристической
функции.
2)
Рассмотрим произвольный элемент
 ,
, Т.о.
Т.о.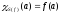 ч.т.д.
ч.т.д.
Пусть Р(х)– высказывательная форма с единственным свободным параметром х, обозначающим элементы множества А.
Пример:
Пусть
А– множество целых чисел, а
 такое,
что х – четное число.
такое,
что х – четное число.
Определим
функцию
 следующим
образом:
следующим
образом:
 –
область истинности высказывания Р. В
этом случае
–
область истинности высказывания Р. В
этом случае
 является
характеристической функцией множества
Х.
является
характеристической функцией множества
Х.
Можно
сказать, что высказывательные формы P
и Q
эквивалентны,
если их характеристические функции
 и
и совпадают.
совпадают.
Пусть
имеется высказывательная форма с n
свободными переменными

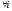
 .
Построим функцию
.
Построим функцию ,
, .
.
Область
истинности для высказывания Р– это
множество
 ,
, .
.
Определение:
n-местный
предикат на множестве А– это функция,
определенная на множестве
 ,
принимающая значения {0,1}.
,
принимающая значения {0,1}.
Определение:
n-местное
отношение на множестве А– это подмножество
множества
 .
.
Замечание:
n-местный
предикат на А– это одноместный предикат
на
 .
.
Между
n-местными
отношениями на А и n-местными
предикатами на
 существуют взаимнооднозначные отношения.
существуют взаимнооднозначные отношения. ,
, .
.
Пусть
имеется высказывательная форма с n
элементами
 ,
тогдаn-местный
предикат
,
тогдаn-местный
предикат
 и
область истинностиR
для высказывания P
могут каждый однозначно определить эту
форму.
и
область истинностиR
для высказывания P
могут каждый однозначно определить эту
форму.
Операции над подмножествами и одноместными предикатами
Пусть
отображение f
и g
 -
одноместные предикаты; определим
следующие операции над ними:
-
одноместные предикаты; определим
следующие операции над ними:
1.

2.

3.
 ;
;
4.
 -тождественно
равно 0 на А;
-тождественно
равно 0 на А;
5.
 -тождественно
равно 1 на А;
-тождественно
равно 1 на А;
Теорема.
Пусть X и Y – 2 произвольных подмножества множества А, тогда:
1.
 ;
;
2.
 ;
;
3.
 ,
где
,
где ;
;
4.
 ;
;
5.
 ;
;
Доказательство.
Рассмотрим произвольное
 :
:

=


![]()
![]() =
=
 =
=
2.
Рассмотрим произвольное
 :
:
=


 =
=
 =
=
3.

Следствие:
Пусть
имеется булево тождество, в которое
входят только связки
 ,
, ,
,
 ,
тогда, если вместо переменных подставить
произвольные подмножества множества
А и заменить
,
тогда, если вместо переменных подставить
произвольные подмножества множества
А и заменить
 на
на ,
а 0 и 1 на
,
а 0 и 1 на и
А, то получится верное равенство.
и
А, то получится верное равенство.
Операция
 - исключающее или.
- исключающее или.
Для
множеств X
и Y
определяется операция “симметрическая
разность”
 .
На самом деле операция
.
На самом деле операция над предикатами соответствует операции
над предикатами соответствует операции над множествами.
над множествами.
Булевы функции
Определение.
БФ
от n
переменных– это отображение
 .
.
Теорема.
Каждую БФ можно выразить через операцию V,, .
Доказательство.
Пусть f:{0,1}n {0,1} – БФ от n переменных
1) Если
 (x1,x2,…,xn){0,1}n
f(x1…xn)=0,то
f(x1…xn)=x1
(x1)
(x1,x2,…,xn){0,1}n
f(x1…xn)=0,то
f(x1…xn)=x1
(x1)
2) Пусть функция f тождественно
Рассмотрим
,x{0,1}.
Обозначим x
=

Для любого набора (1,2,…,n), для которого функция f принимает значение 1, мы рассмотрим выражение вида:
x11x22…xnn
Дизъюнкция всех этих выражений даёт булеву функцию f
Докажем это:S={(1…n) {0,1}n|f(1…n)=1 }
Тогда g(x1…xn)= V(x11x22…xnn) (1…n)S
g(x1…xn)=f(x1…xn)
Определим, при каких значениях x1…xn функция g=1 (1…n)S,такой что X11Х22…Хnn=1
X11Х22…Хnn=1 i Хi=i.
Т.е. g(x1…xn)=1 для тех и только тех наборов, которые входят в множества S.
С другой стороны, f(x1…xn)=1 для тех и только для тех, которые входят в множество S.
Т.е. функции f и g принимают значения 1 и 0 на одних и тех же наборах f=g.
Следствие:
Каждую БФ можно выразить, используя только 2 операции: или
Замечание:
Представленная
в теореме функция g
называется совершенной дизъюнктивной
нормальной формой (СДНФ). Исходя из
тождества
 =x
строится совершенная конъюнктивная
нормальная форма. Возьмём СДНФ:
=x
строится совершенная конъюнктивная
нормальная форма. Возьмём СДНФ:
V
Тогда
¬V =
^(¬
=
^(¬ )=
)=
(1…n): (1…n):
f(1…n)=1 f(1…n)=1
= 

f(x1…xn)= ( f(x1…xn))
f(x1…xn)= ( f(x1…xn))
Пусть
ρ(x1…xn)=
f(x1…xn),
тогда ρ(x1…xn)=
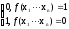
ρ(x1…xn)=
 (1…n):
f(1…n)=0
(1…n):
f(1…n)=0
f=-(ρ(x1…xn))=
( )=
)=
=
 (1…n):
f(1…n)=0
(1…n):
f(1…n)=0
Минимизация булевых функций
Булева функция может быть задана в виде булевых переменных, соединенных знаками операций (т.е. в виде некоторой формулы). Под сложностью булевой функции будем понимать количество вхождений символов переменных в формулу, описывающую эту функцию.
ПРИМЕР:
Сложность
булевой функции

 =15,
а сложность функции
=15,
а сложность функции
 =3.
В то же время обе эти формулы описывают
одну и ту же булеву функцию.
=3.
В то же время обе эти формулы описывают
одну и ту же булеву функцию.
Возникает задача минимизации булевых функций. Эффективных методов решения этой задачи в общем виде не существует. Поэтому мы ограничимся рассмотрением формул специального вида. Мы будем рассматривать формулы, содержащие лишь операции отрицания, дизъюнкции и конъюнкции.
Определение:
Дизъюнктивной
нормальной формой (ДНФ) называется
формула, имеющая вид дизъюнкции некоторых
конъюнкций:
 (для удобства знак
(для удобства знак опускаем).
опускаем).
Определение:
Минимальной ДНФ (МДНФ) функции f называется ДНФ, содержащая минимально возможное число вхождений символов переменных среди всех ДНФ, реализующих f.
Определение:
Булева
функция
 является импликантом функции
является импликантом функции ,
если для всякого набора
,
если для всякого набора значений аргументов выполнено неравенство:
значений аргументов выполнено неравенство:
 .
Данное условие может быть записано в
эквивалентном виде:
.
Данное условие может быть записано в
эквивалентном виде:
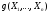 =
= .
.
Определение:
Импликант называется простым, если он представляет собой конъюнкцию переменных (возможно с отрицаниями) и любая конъюнкция, полученная из него в результате вычеркивания любой переменной, импликантом не является.
