1.2 Краевые условия задачи

В задачах теории поля единственность решения уравнения переноса (1.1.14) обеспечивается заданием краевых условий задачи: начального поля искомой величины в момент времени, выбранный за нулевой :

, (1.2.1)

и граничных условий, которые в задачах теории поля чаще всего формулируются в виде следующих условий на границе (или ее части) области определения задачи:

а) задано поле температур−так называемое главное граничное условие:,; (1.2.2)

б) задано обобщенное условие сложного теплообмена [1] − или естественное граничное условие:

, (1.2.3)

входящие в (1.2.3) слагаемые описывают теплообмен: - кондуктивный;-конвективный (на внешнихи внутреннихповерхностях элемента);− радиационный (внешний и внутренний);− внешний поверхностный источник тепла, зависящий в общем случае от времени. Поверхностьпредставляет собой-й участок внешней или внутренней границ, и в совокупности образует oбe границы области в целом (в случае ее многосвязности).

В задачах теплопроводности принято граничные условия задачи подразделять на четыре рода, а именно:

1-го рода – Т(х_i,τ) = f(х_i), при этом функция может быть задана в виде константы, например, Т(х_i,τ) = Т_с;

2-го рода – (q_λ + q_c)_Si = 0; где q_c – внешний поверхностный источник энергии (Вт/м²), чаще всего равный константе; кондуктивный компонент описывается законом Фурье;

3-го рода – (q_λ + q_α)_Si = 0; связывает кондуктивный и конвективный удельные потоки на поверхности S_i; конвективный компонент описывается законом Ньютона;

4-го рода – полагаются непрерывными температурные поля и удельные тепловые потоки на границе раздела двух сред: Т_i(x_i)_Sk = T_j(x_j)_Sk; q_λi(x_i)_Sk = q_λj(x_j)_Sk.

По определению граничное условие – это условие энергетического сопряжения на внешней поверхности тела при наличии двух (трех) механизмов теплообмена или на границе раздела двух сред. По сути – это условия теплового баланса на поверхности раздела.

Кондуктивный компонент описывается законом Фурье и в обобщенной криволинейной системе координат согласно (1.1.5) имеет вид:

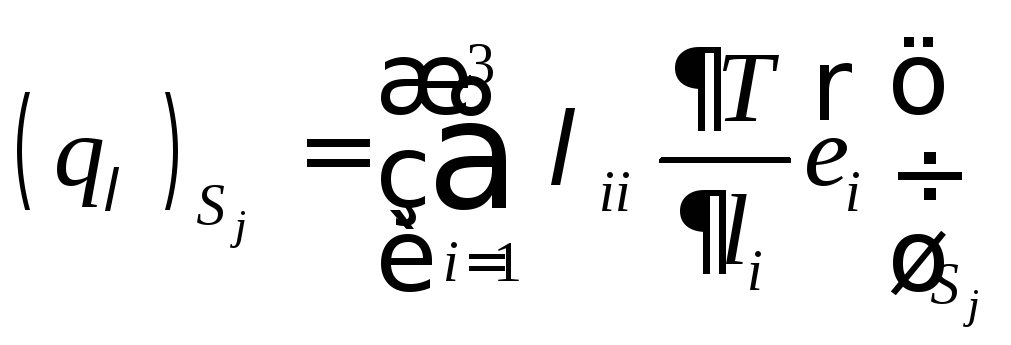. (1.2.4)

Конвективный компонент в аналитической теории теплопроводности обычно выражают законом Ньютона [20]:

, (1.2.5)

где – коэффициент теплообмена при естественной или смешанной конвекциях, вопросам расчета которого посвящена обширная литература [19–29], но в аналитической теории теплопроводности он полагается заданным в виде некоторого числа; Т_ср.– температура среды или теплоносителя.

Радиационный компонент нелинейно зависит от температуры и, согласно закону Стефана-Больцмана [30]:

, (1.2.6)

где− полусферическая интегральная степень черноты поверхности;= 5,67·10^-8 Вт/м²К⁴ – постоянная Стефана-Больцмана.

Запишем естественное граничное условие (1.2.3) с учетом (1.2.4)−(1.2.6) в обобщенном виде:

, (1.2.7)

где под понимается величина:

. (1.2.8)

В целях линеаризации граничного условия радиационный компонент зачастую представляют в виде, аналогичном конвективному компоненту [20, 24, 32]:

,

где , и затем объединяют с конвективным компонентом, вводя суммарный коэффициент теплообмена . Величинурассчитывают, полагая− некоторой характерной температуре изучаемого процесса [32]. Если при описании внешнего радиационного теплообмена с такой процедурой линеаризации можно согласиться, то для внутреннего теплообмена подобная замена нежелательна, так как в этом случае радиационный компонент рассчитывается с учетом оптико-геометрического фактора – средних разрешающих угловых коэффициентах излучения, обусловленного взаимным расположением теплообменивающихся поверхностей и их степеней черноты.