Глава 1. Краевые задачи теории поля

Физические процессы обычно описываются дифференциальными уравнениями различного порядка с начальными и граничными условиями к ним. В зависимости от искомой величины − векторной или скалярной − решение уравнения описывает в общем случае пространственно-временное распределение этой величины, называемое ее векторным или скалярным полем. В этой главе будут приведены выражения дифференциального уравнения переноса (типа известных из курса дифференциальных уравнений уравнения Лапласа и Пуассона) и граничных условий к ним в обобщенной криволинейной ортогональной системе координат и дана краткая характеристика аналитических методов его решения.

1.1 Уравнение переноса в обобщенной криволинейной системе координат

Диапазон физических задач, решаемых с помощью этого уравнения, достаточно велик. Приведем лишь некоторые из встречающихся в инженерной практике: теплопроводность [1], фильтрация в пористой среде [2, 3], невихревое течение идеальной жидкости [5], задачи механики сплошных сред [4, 6] и электромагнетизма [7].

Вид нестационарного уравнения переноса хорошо известен из курса дифференциальных уравнений [9]:

i = 1, 2, 3. (1.1.1)

где ∆− лапласиан (дифференциальный оператор 2-го порядка); u(x_i,τ) − искомая функция, описывающая поле значений физической величины; w(x_i,τ) − задаваемая функция координат и времени; τ − время; k, η − коэффициенты, физический смысл которых обусловлен природой исследуемого процесса; x_i, τ − текущие переменные.

Размерность и геометрическая форма области существования функции u(x_i,τ) определяются, очевидно, геометрией изучаемого объекта (конструкции или ее элемента) Поэтому целесообразно записать уравнение (1.1.1) в обобщенной криволинейной ортогональной системе координат, что даст возможность применять его к объекту любой геометрии и размерности. Как станет ясно впоследствии, такая форма записи будет полезна при использовании метода конечных элементов (МКЭ) для решения уравнения.

Введем некоторую криволинейную ортогональную систему координат ξ_i (i=1,2,3) , единичные орты которой равны

. (1.1.2)

Здесь − радиус-вектор точки с координатами, а модуль его производной по криволинейной координате, называемый параметром Ляме, равен:

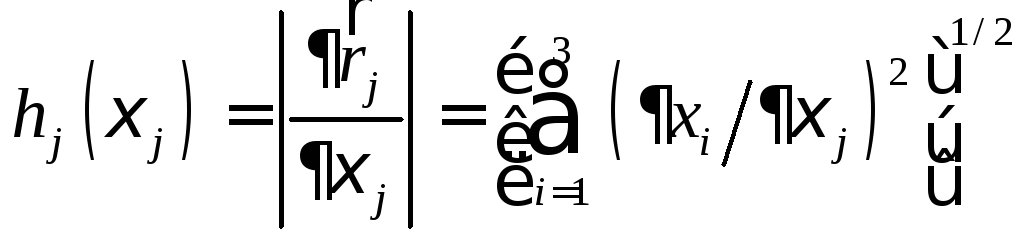, j =1, 2, 3. (1.1.3)

Элементы длины, площади поверхности и объема в этой системе координат связаны с приращениями координат через параметры Ляме:

; ;(1.1.4)

Градиент функции есть вектор, который в криволинейной системе координат описывается формулой [9]:

. (1.1.5)

Оператор Лапласа может быть записан так:

.

С учетом ортогональности системы координат подстановка (1.1.5) в последнее выражение даст [11, 25]:

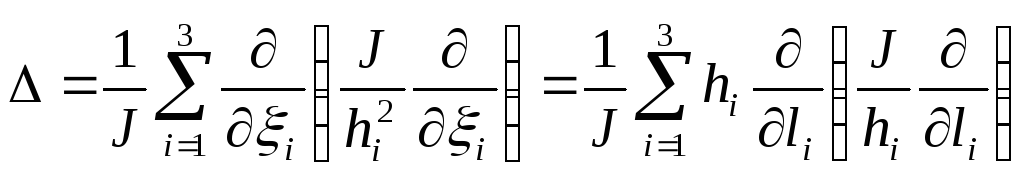, (1.1.6)

где − якобиан преобразования декартовой системы координат в криволинейную, равный произведению параметров Ляме:

. (1.1.7)

Таким образом, дифференциальное уравнение (1.1.1) в обобщенной криволинейной ортогональной системе координат будет иметь вид:

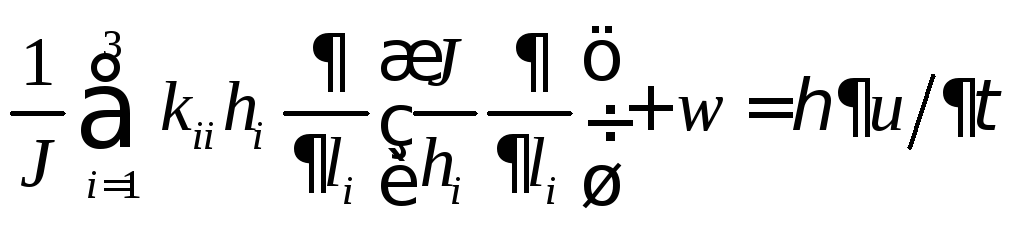. (1.1.8)

Конкретный вид уравнения (1.1.8) в той или иной системе координат можно получить, если задать функции связи между декартовыми и криволинейнымикоординатами.

Очевидно, что в декартовой системе , в силу чего все параметры Ляме; следовательно,и. В итоге на основании (1.1.8) имеем уравнение переноса в декартовой системе координат:

. (1.1.9)

Связь между координатами декартовой и цилиндрической системами координат −,,− выражается известными соотношениями [11]:

; ; .

Подставляя производные этих функций связи в (1.1.3), найдем параметры Ляме и якобиан:

; ; ;, (1.1.10а))

что после внесения их в уравнение (1.1.8) дает:

. (1.1.11)

В случае сферической системы координат – , (азимутальный угол),(полярный угол) – связь между координатами также известна [11]:

; ; .

Параметры Ляме и якобиан будут следующими:

; ; h₃ = r ; , (1.1.10 б))

и уравнение примет вид:

. (1.1.12)

Заметим, что согласно (1.1.4):

. (1.1.13)

Из курса аналитической геометрии [11] известно, что орты криволинейной ортогональной системы координат направлены по нормали и по касательнымик соответствующим координатным линиям и не сохраняют свои направления в пространстве при изменении координат точки, оставаясь при этом ортогональными. Введем понятиепорядка симметрии S системы координат, равном числу изменяющих свое направление ортов при изменении координат точки. Тогда полученные выражения дифференциальных уравнений (1.1.9), (1.1.11) и (1.1.12) могут быть представлены в обобщенном виде:

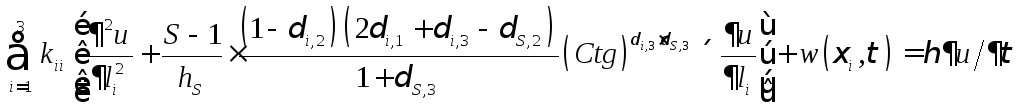. (1.1.14)

Здесь − символ Кронекера, равный, как известно,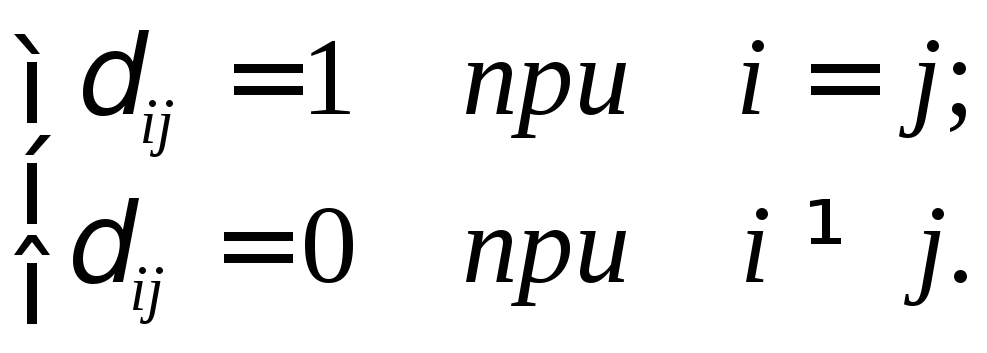

При записи (1.1.14) учтено, что для цилиндрической системы S = 2 –, длясферической S = 3 − все , а длядекартовой вместо S = 0 (все ) формально положеноS = 1.

Обобщенное нестационарное уравнение (1.1.14) является математической моделью процесса переноса независимо от его физического содержания. Для конкретизации процесса достаточно задать физический смысл входящих в уравнение коэффициентов, что однозначно определит и физическую природу функции u(x_i,τ). В электрической интерпретации, например, соответствующие величины будут связаны с величинами проводимости, источника зарядов и потенциала [7]. В интересующем нас процессе теплопроводности коэффициенты k_ii являются главными значениями тензора анизотропной теплопроводности [2, 24], η = c_pρ − объемная теплоемкость, w − объемная плотность мощности внутреннего источника (стока) тепла, а искомая скалярная величина u(ξ_i,τ) − температура .