
- •А.В. Румянцев
- •Содержание
- •Глава 6. Программная реализация метода
- •Глава 1. Краевые задачи теории поля
- •1.1 Уравнение переноса в обобщенной криволинейной системе координат
- •1.2 Краевые условия задачи
- •1.3* Краткая характеристика методов решения краевой задачи
- •Глава 2. Метод конечных элементов в краевых
- •2.1 Методы взвешенных невязок
- •2.2 Основная концепция метода конечных элементов
- •Глава 3. Геометрические аспекты мкэ
- •3.1 Типы конечных элементов. Базовый каталог элементов
- •3.2 Дискретизация области на элементы
- •А) с разными (вид сверху); б) с одинаковыми.
- •Цифры – это номер элемента по каталогу
- •3.3 Нумерация элементов и узлов
- •3.4 Индексация узлов и формирование таблицы входных данных
- •Осесимметричной детали
- •Геометрическая часть таблицы входных данных
- •Глава 4. Математическое описание элемента
- •4.1 Метод Крамера
- •4.2 Метод Лагранжа
- •4.3 Обобщенный метод Крамера-Лагранжа
- •4.4 Эрмитовы элементы
- •4.5 Свойства базисных функций элемента
- •Глава 5. Вычислительные аспекты мкэ
- •5.2 Матричное представление элементного вклада
- •Производные базисных функций
- •5.3 Формирование глобальных матриц для исследуемой области
- •А) Сокращенная
- •5.4 Стандартизация матриц элементов
- •5.5 Естественная система координат
- •5.6 Средние температуры элемента
- •Глава 6. Программная реализация мкэ
- •6.1 Задание краевых условий задачи
- •6.2 Решение системы динамических уравнений
- •Временная циклограмма q(τ)
- •6.З Учет температурной зависимости теплофизических параметров
- •6.4 Радиационный компонент теплообмена
- •6.5 Сходимость, полнота и согласованность, точность
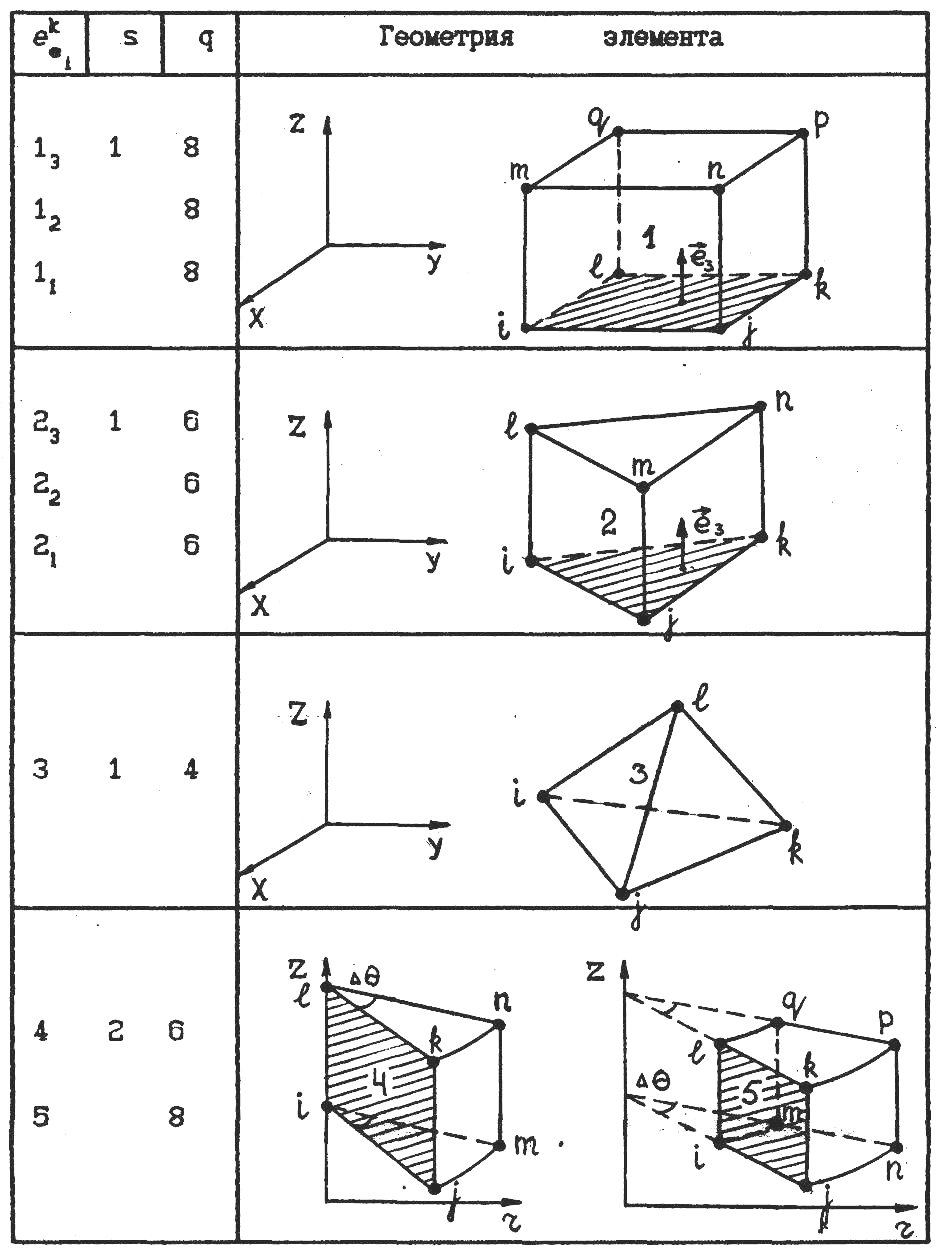
- •Базовый каталог объемных элементов
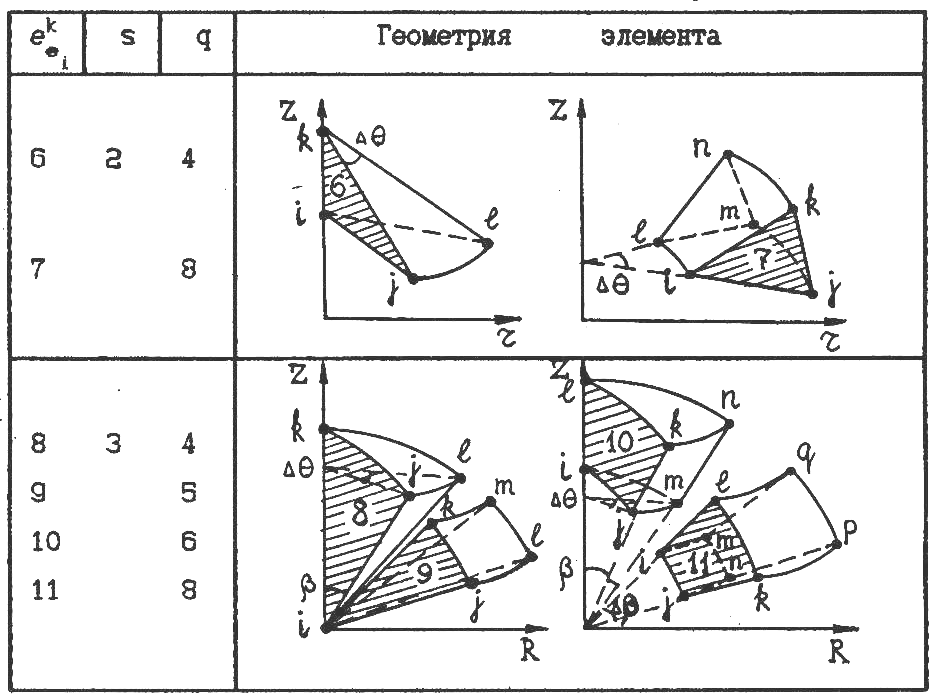
- •Осесимметричные объемные элементы
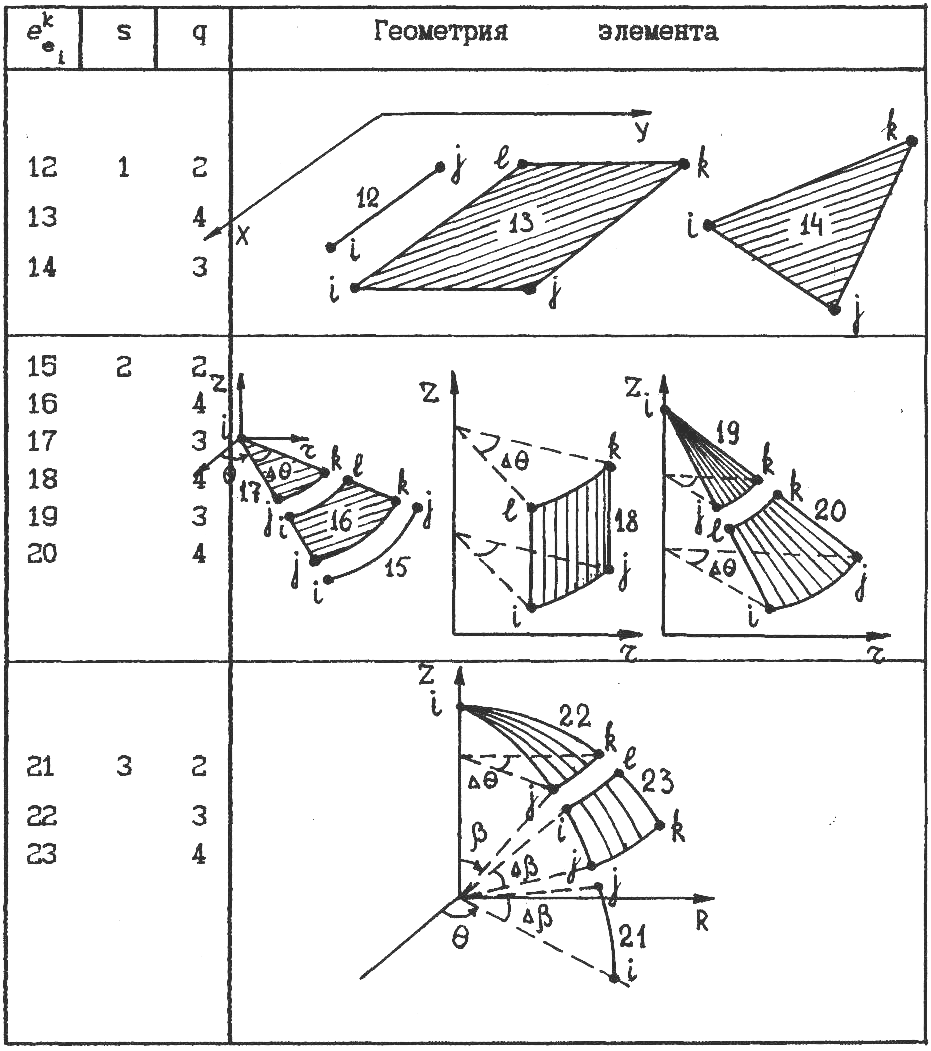
- •Базовый каталог одно- и двумерных элементов
Базовый каталог объемных элементов
Осесимметричные объемные элементы

Базовый каталог одно- и двумерных элементов
Осесимметричные
одно- и двумерные элементы получается
поворотом на
![]() порождающих
порождающих![]() -x
одномерных элементов.
-x
одномерных элементов.
Приложение 2
Методика получения стандартизованных матриц элемента
Возьмем
для примера 2-ой элемент базового
каталога и применим к нему обобщенный
метод Крамера-Лагранжа, поскольку он
лишь частично образован координатными
плоскостями
![]() и
и![]() .
Присвоим узлам индексы
.
Присвоим узлам индексы![]() ,
соблюдая
правило обхода против
часовой стрелки.
,
соблюдая
правило обхода против
часовой стрелки.
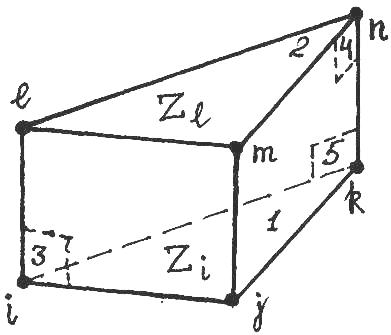 В
основании треугольной прямой призмы
лежит симплекс-треугольник, трансляцией
которого вдоль орта
В
основании треугольной прямой призмы
лежит симплекс-треугольник, трансляцией
которого вдоль орта
![]() на расстояние
на расстояние![]() образован объемный элемент. Точно так
же можно считать, что элемент образован
трансляцией верхнего
образован объемный элемент. Точно так
же можно считать, что элемент образован
трансляцией верхнего
основания
по орту
![]() .
Базисные функции легко находятся по
обобщенному методу Крамера-Лагранжа,
т.е. умножением базисных функций
симлекс-треугольников
.
Базисные функции легко находятся по
обобщенному методу Крамера-Лагранжа,
т.е. умножением базисных функций
симлекс-треугольников![]() и
и![]() на полином Лагранжа
на полином Лагранжа![]() (см. п. 4.3):
(см. п. 4.3):
![]() ,
при
,
при
![]() (П.2.1)
(П.2.1)
Полиномы Лагранжа имеют вид:
![]() ;
;
![]() .
(П.2.2)
.
(П.2.2)
Функции для симплекс-треугольника возьмем в виде (4.1.7):
![]() ,
,
![]() ,
(П.2.3)
,
(П.2.3)
![]() –удвоенная
площадь треугольника (см. 4.1.3). Конкретные
значения коэффициентов в (П.2.3) нас пока
не интересуют. Правильность базисных
функций узлов элемента гарантирована
использованием обобщенного метода
Крамера-Лагранжа.
–удвоенная
площадь треугольника (см. 4.1.3). Конкретные
значения коэффициентов в (П.2.3) нас пока
не интересуют. Правильность базисных
функций узлов элемента гарантирована
использованием обобщенного метода
Крамера-Лагранжа.
Найдем
производные базисных функций по
текущим переменным
![]() :
:
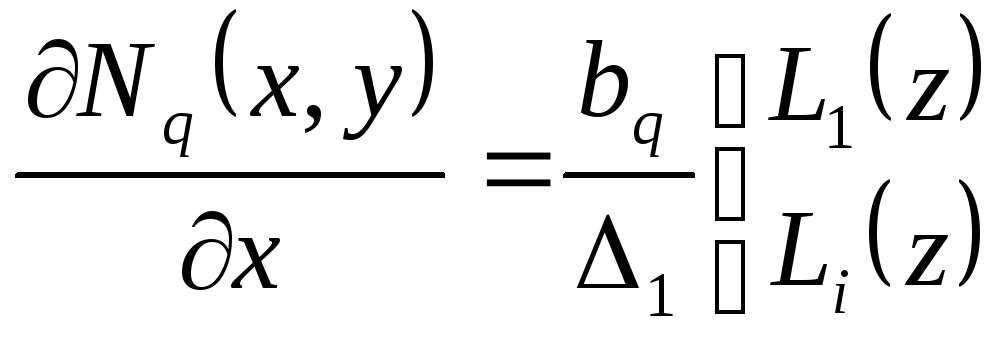 ;
;
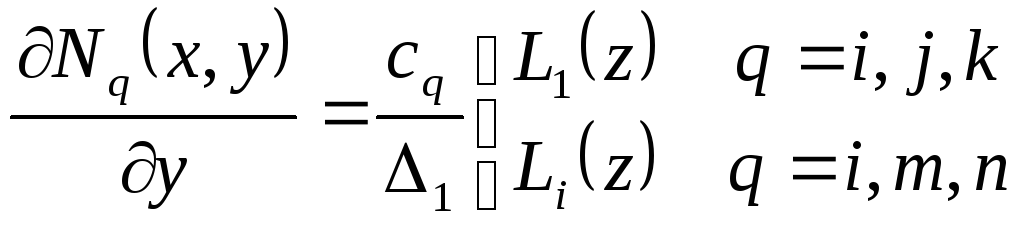 ;
;
![]() .
(П.2.4)
.
(П.2.4)
Элементарный объем представим в виде
![]() ,
(П.2.5)
,
(П.2.5)
так
как производные по
![]() и
и![]() есть постоянные, умножаемые на полином
есть постоянные, умножаемые на полином![]() .
.
Найдем объемную часть матрицы теплопроводности, подставляя в (5.3.2) производные (П. 2.4) с учетом (П. 2.5):
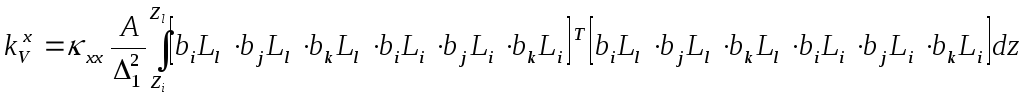 (П.2.6)
(П.2.6)
![]() .
.
Типичные интегралы:
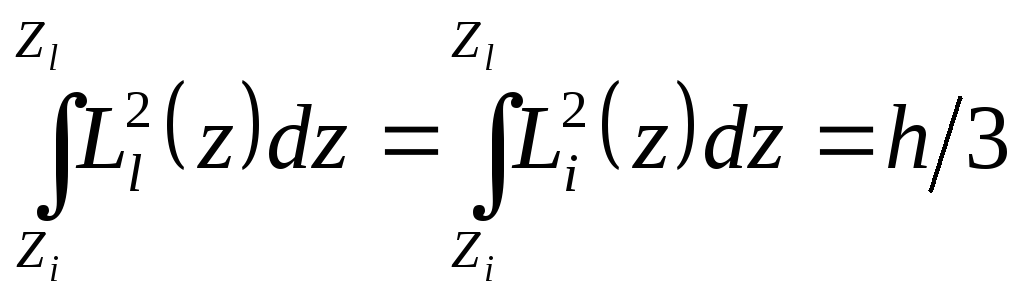 ;
;
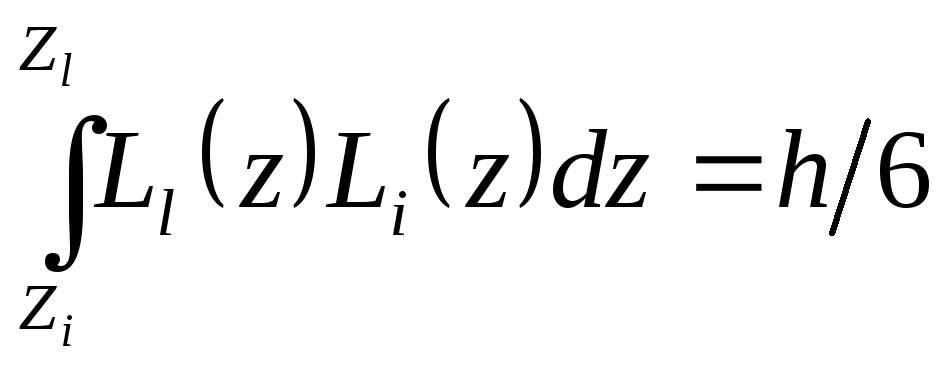 .
(П.2.7)
.
(П.2.7)
Компонент
![]() будет идентичен
будет идентичен![]() ,
если
,
если![]() заменить на
заменить на![]() .
Поэтому запишем эти части матрицы в
общем виде:
.
Поэтому запишем эти части матрицы в
общем виде:
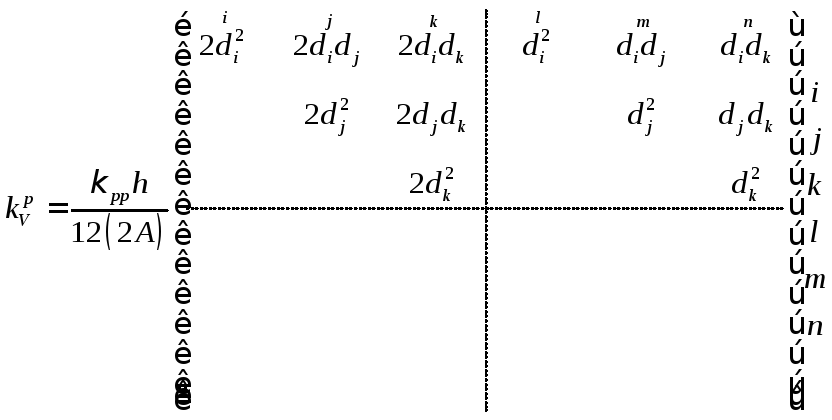 (П.2.8)
(П.2.8)
Здесь
при
![]() ,
,![]() ;
при
;
при![]() ,
,![]() .
.
Так
как производная по
![]() зависит только от
зависит только от![]() ,
то при интегрировании по объему
целесообразно перейти к плоским
,
то при интегрировании по объему
целесообразно перейти к плоским![]() -координатам:
-координатам:
![]() .
.
Производя перемножение сцепленных матриц, и интегрируя с учетом (5.3.8), получим окончательно:
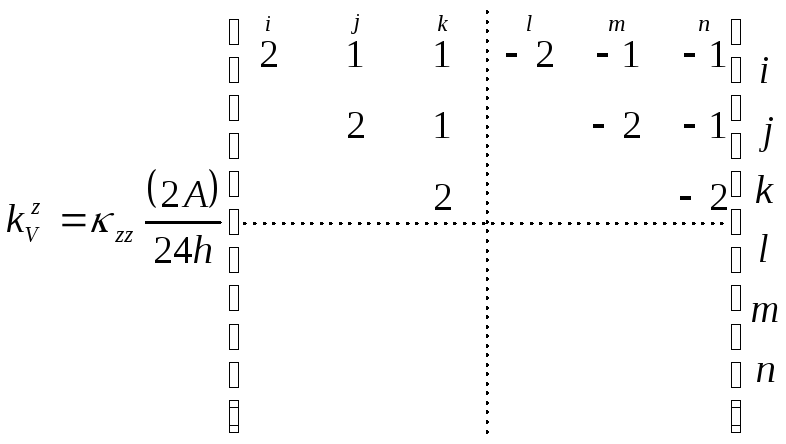 (П.
2.9)
(П.
2.9)
Таким образом, объемная часть матрицы теплопроводности элемента будет равна:
![]() .
(П.2.10)
.
(П.2.10)
Полученные
результаты (П.2.8) и (П.2.9) рекомендуется
проверить на правильность размерности,
которая должна быть
![]() :
:
![]() ;
;
![]() ;
;![]() ;
;![]() .
.
В
итоге имеем
![]() .
.
Матрицы
![]() -
стандартизованы и поэтому заносятся
в программу. Они станут числовыми, если
символы заменить их числовыми значениями,
определяемыми по узловым координатам
-
стандартизованы и поэтому заносятся
в программу. Они станут числовыми, если
символы заменить их числовыми значениями,
определяемыми по узловым координатам![]() ,
а коэффициенты теплопроводности – на
их величины согласно физическому
каталогу.
,
а коэффициенты теплопроводности – на
их величины согласно физическому
каталогу.
Поверхностные
части матрицы теплопроводности
![]() (
(![]() пo числу поверхностей) определяются
согласно формуле (5.1.3). Присвоим
поверхностям элемента номера:
пo числу поверхностей) определяются
согласно формуле (5.1.3). Присвоим
поверхностям элемента номера:
![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() .
.
Матрицы
для поверхностей 1 и 2 будут отличаться
только коэффициентами
![]() ,
и индексами строк и столбцов, так как
этим поверхностям принадлежат разные
узлы. Интегрирование по
,
и индексами строк и столбцов, так как
этим поверхностям принадлежат разные
узлы. Интегрирование по![]() можно провести с помощью
можно провести с помощью![]() -координат.
Базисные функции узлов найдем, приравнивая
текущую
-координат.
Базисные функции узлов найдем, приравнивая
текущую![]() для первой плоскости и
для первой плоскости и![]() -
для второй. В итоге будем иметь:
-
для второй. В итоге будем иметь:
![]() ;
;
![]() ;
;![]() ;
;
(П.2.11)
![]() ;
;
![]() ;
;![]() ;
;
Подставим найденные базисные функции в (5.1.3) и проинтегрируем согласно (5.3.8). Получим:
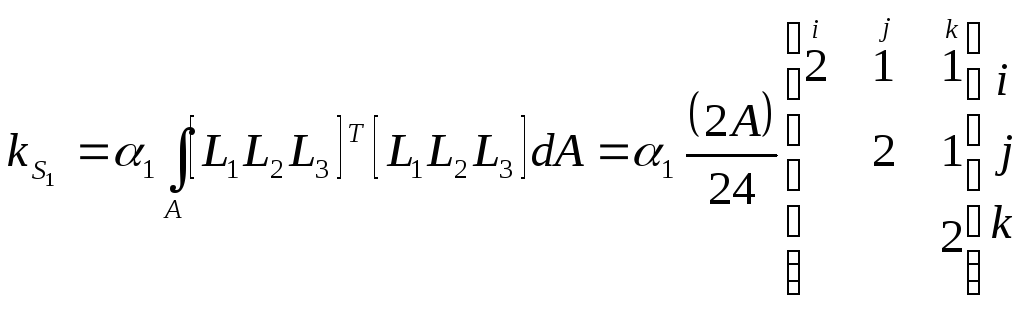 .
(П.2.11)
.
(П.2.11)
По аналогии:
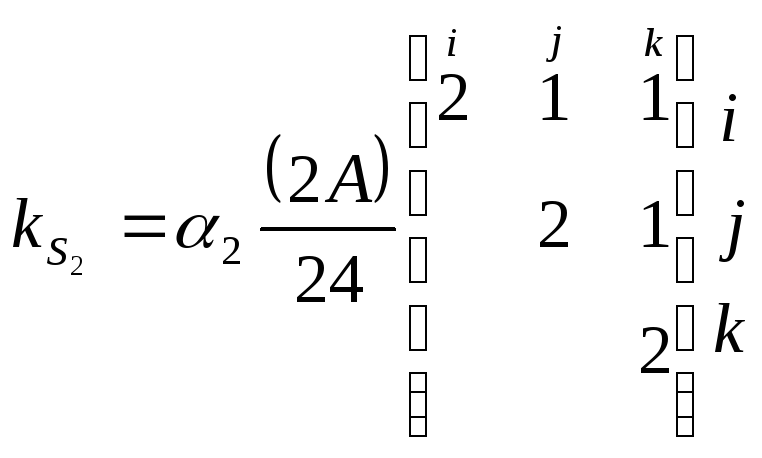 .
(П.2.12)
.
(П.2.12)
На
самом деле эти матрицы имеют ранг,
равный шести, но мы не стали загромождать
их выражения нулевыми строками и
столбцами. Номера узлов покажут их
место в глобальной матрице
![]() .
.
Матрицы
для остальных поверхностей находятся
так же легко благодаря переходу к
плоским
![]() -
координатам. Типичные интегралы будут
иметь вид:
-
координатам. Типичные интегралы будут
иметь вид:
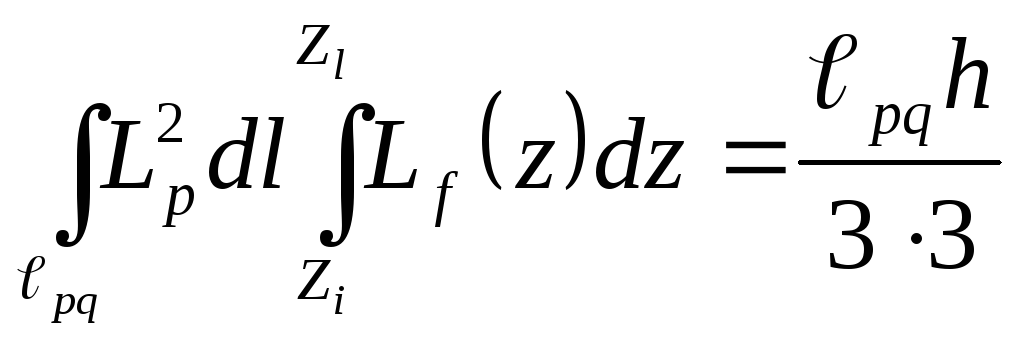 ;
;
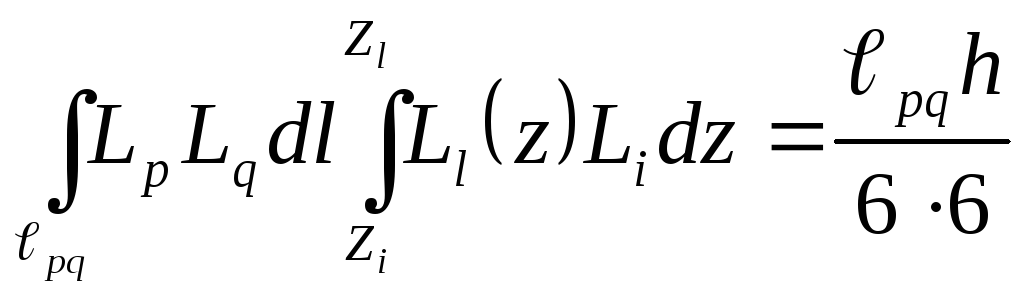 ;
;
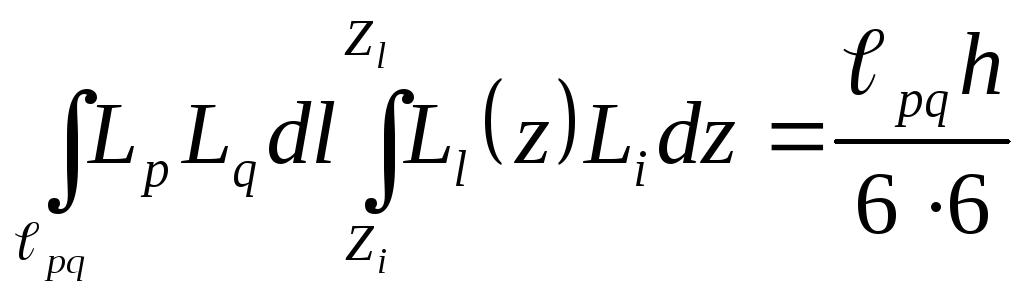 ,
(П.2.13)
,
(П.2.13)
![]() ,
,
![]() ,
,![]() ;
;![]() ,
,![]() .
.
Поверхностные
сокращенные матрицы для
![]() будут иметь одинаковый вид и отличаются
коэффициентом
будут иметь одинаковый вид и отличаются
коэффициентом![]() ,
длиной
,
длиной![]() и индексами ненулевых строк и столбцов:
и индексами ненулевых строк и столбцов:
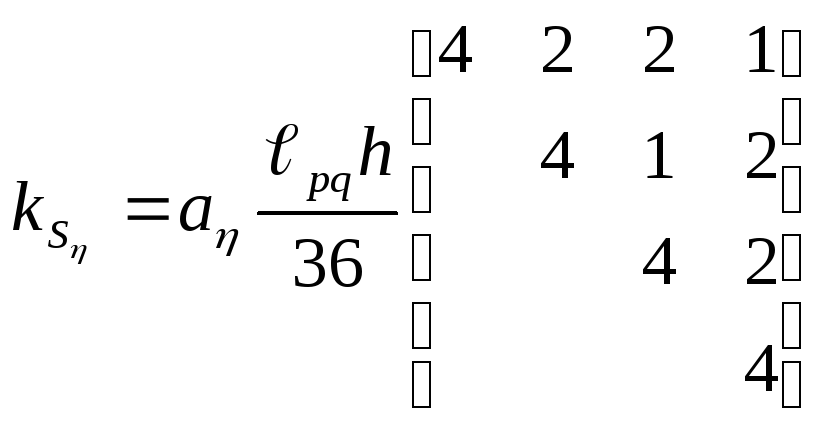 ,
(П.2.14)
,
(П.2.14)
![]() ;
;
![]() ,
,![]() ;
;![]() .
.
Для определения матрицы достаточно строкам и столбцам матрицы (П.2.14) присвоить индексы соответствующей плоскости. Формула (П.2.14), будучи стандартизованной, также заносится в программу.
Матрица
теплоемкости (5.1.5) находится так же
легко, только интегрирование с помощью
![]() -
координат ведется не по
-
координат ведется не по![]() ,
а по
,
а по![]() ,
а полином Лагранжа
,
а полином Лагранжа![]() интегрируется по
интегрируется по![]() .
Типичные интегралы идентичны интегралам
(П.2.13):
.
Типичные интегралы идентичны интегралам
(П.2.13):
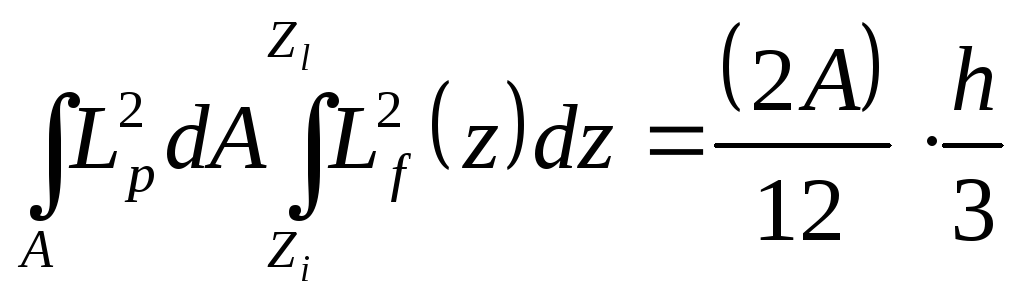 ;
;
![]()
(П.2.15)
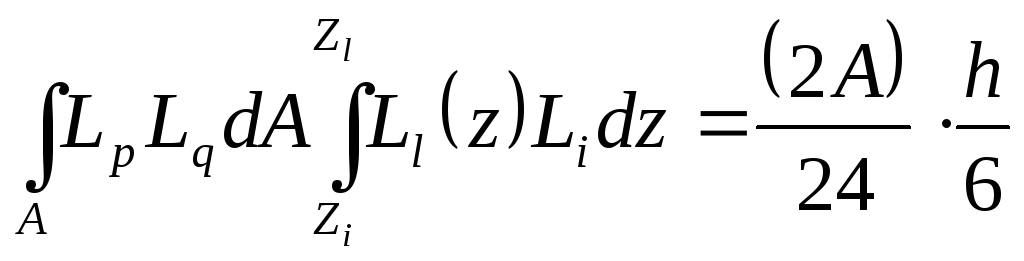 ,
,
![]() .
.
Таким образом, матрица теплоемкости будет равна:
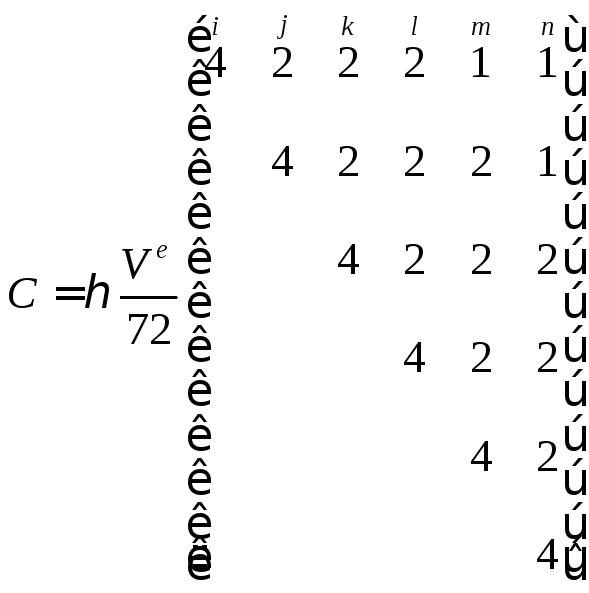 ,
(П.2.16)
,
(П.2.16)
где
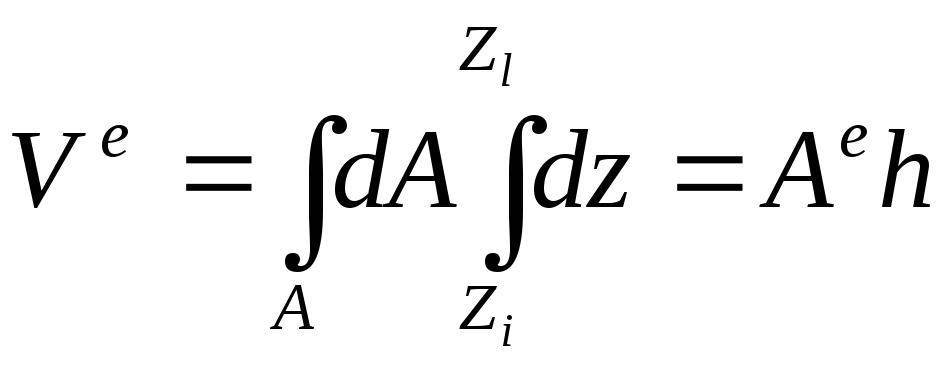 – объем элемента.
– объем элемента.
Умножением
элементов матрицы на числовые значения
![]() и объема элемента, сокращенная матрица
теплоемкости превращается в числовую
и сразу заносится в глобальную
соответственно номерам узлов.
и объема элемента, сокращенная матрица
теплоемкости превращается в числовую
и сразу заносится в глобальную
соответственно номерам узлов.
Найдем объемную часть вектора тепловой нагрузки согласно (5.1.8):
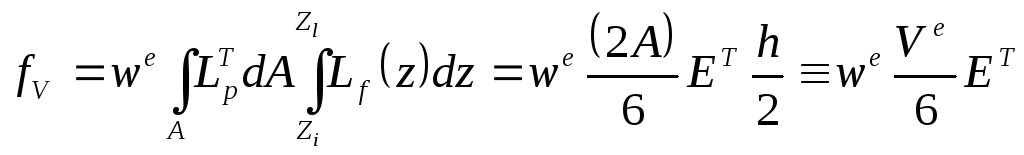 ,
(П.2.17)
,
(П.2.17)
где
![]() –
единичный вектор-столбец.
–
единичный вектор-столбец.
Из
(П.2.17) видно, что распределение
![]() по узлам элемента равномерное, независимо
от его геометрии. Это означает, что
желательно иметь элемент с примерно
равными ребрами, чтобы распределение
(П.2.17) было приближено к реальному
физическому. Числовой вектор (П.2.17)
заносится в глобальный вектор
по узлам элемента равномерное, независимо
от его геометрии. Это означает, что
желательно иметь элемент с примерно
равными ребрами, чтобы распределение
(П.2.17) было приближено к реальному
физическому. Числовой вектор (П.2.17)
заносится в глобальный вектор![]() .
.
Поверхностный компонент тепловой нагрузки находится по (5.1.9) так же просто, как и объемный:
![]() .
(П.2.18)
.
(П.2.18)
По аналогии
![]() .
(П.2.19)
.
(П.2.19)
Остальные компоненты найдем по формулам:
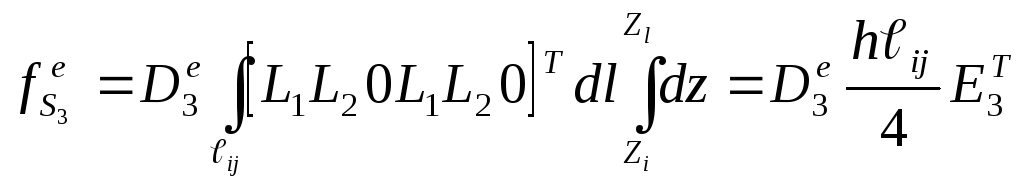 ;
(П.2.20)
;
(П.2.20)
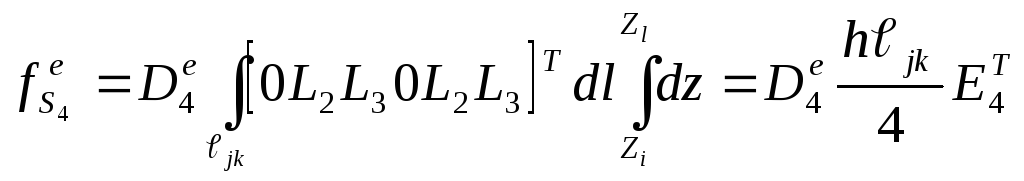 ;
(П.2.21)
;
(П.2.21)
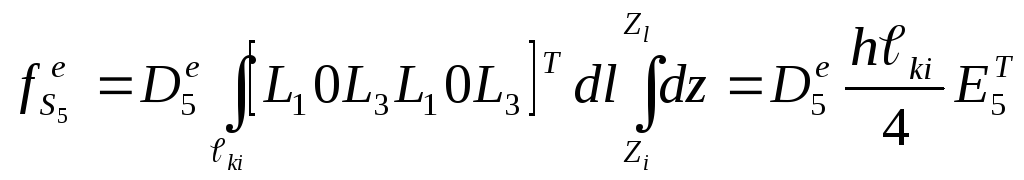 .
(П.2.22)
.
(П.2.22)
Превращая
вектор-столбцы в числовые, их заносят
соответственно номерам узлов в глобальный
вектор
![]() .
.
Таким образом, все стандартизованные и программируемые матрицы для 2-го элемента базового каталога найдены. Остается найти средние температуры по формулам (5.4.1), поскольку они тоже должны находиться программно:
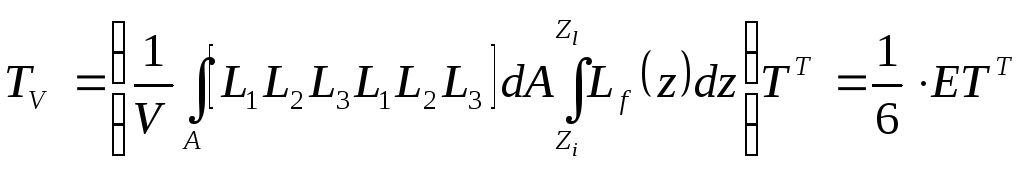 ,
(П.2.23)
,
(П.2.23)
где
![]() –
единичная строка,
–
единичная строка,![]() –
вектор-столбец узловых значений
температуры.
–
вектор-столбец узловых значений
температуры.
Интегралы, которые следует взять для вычисления средних поверхностных температур элемента, фактически уже взяты – это выражения (П.2.18) – (П.2.22). Остаётся лишь единичные вектор-столбцы заменить на единичные строки и умножить их на вектор-столбец значений температуры в узлах, принадлежащих поверхности. В итоге будем иметь общую формулу для среднеповерхностной температуры:
![]() .
(П.2.24)
.
(П.2.24)
Здесь
![]() –
число узлов, принадлежащих поверхности;
–
число узлов, принадлежащих поверхности;
![]() ,
,
![]() – единичная матричная строка и
температура в узлах, принадлежащих
поверхности, соответственно.
– единичная матричная строка и
температура в узлах, принадлежащих
поверхности, соответственно.
Из выражений (П.2.23) и (П.2.24) видно, что средние температуры находятся как среднее арифметическое температур элемента или плоскости, соответственно:
![]() ;
;
![]() .
(П.2.25)
.
(П.2.25)
Формулы (П.2.23) и (П.2.24) или их аналоги (П.2.25) программируются, так как знание средних температур необходимо при учете температурной зависимости теплофизических свойств материала элемента и радиационного компонента теплообмена.
Описанная процедура стандартизации матриц элемента выполняется для каждого элемента базового каталога.
