6.2 Решение системы динамических уравнений

Задание граничных условий позволяет программно превратить

глобальные матрицы в числовые. В стационарном случае это означает, что

получена система R (по количеству узлов) алгебраических уравнений с числовыми коэффициентами при неизвестных узловых значениях или, которая может быть разрешена с помощью стандартной программы (например, “GELG”, реализующей метод Гаусса).

В нестационарном случае получается система R обыкновенных дифференциальных уравнений первого порядка с числовыми глобальными матрицами [1]:

, , (6.2.1)

с начальным условием, включенным в таблицу данных:

. (6.2.2)

Система уравнений (6.2.1) вместе с (6.2.2) представляет собой известную

Таблица 5

Временная циклограмма q(τ)

Время (мин.)	Номер элемента	Номер поверхности	Величина мощности (Вт)
0 ÷ 30	3 5 12	1 4 3	20 35 74
30 ÷ 60	3 7 14	2 1 6	51 40 62

задачу Коши. Для ее решения применим метод конечных элементов, для чего представим (см. рис. 6.1) временную ось совокупностьюотрезков (элементов), не обязательно одинаковой длины, хотя последнее и удобнее. Криваядает графическое изображение временной зависимости температуры не в отдельном глобальномr-ом узле, а всего вектора значений температуры в R глобальных узлах, т.е. – этовектор-столбец размером . Для отображения этого факта на рисунке применен жирный шрифт.

Используя версию МКЭ, аппроксимирующую функцию на -м временнόм элементе представим в виде:

, (6.2.3)

где – матричная строка базисныхвременных функций;

–вектор-столбец всей совокупности значений температу-

ры в -м и в -м узлах -го временнόго элемента.

В качестве базисных функций возьмем линейную модель, которая в естественной системе временных координат имеет вид:

, ,(6.2.4)

Применив метод Галеркина к дифференциальному уравнению (6.2.1), для -го временнόго элемента получим систему уравнений в интегральной форме:

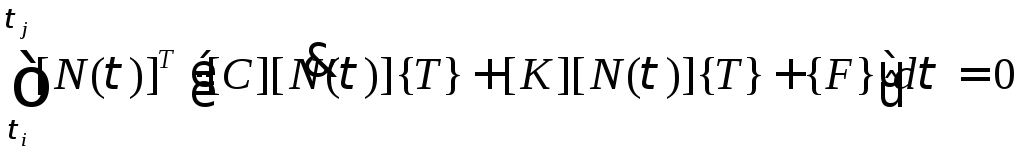. (6.2.5)

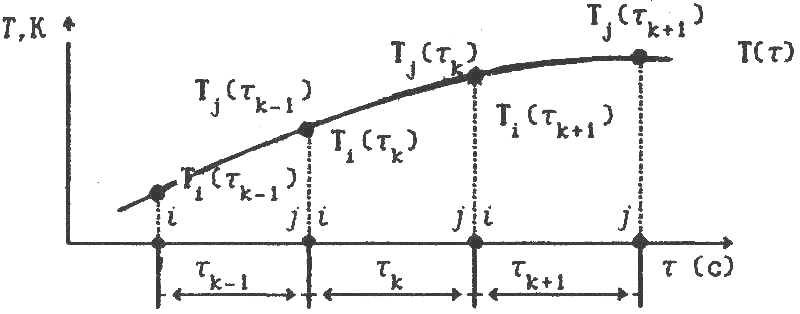
Рис. 6.1

Интегрирование этого выражения с помощью -координат приводит к системе алгебраических линейных уравнений:

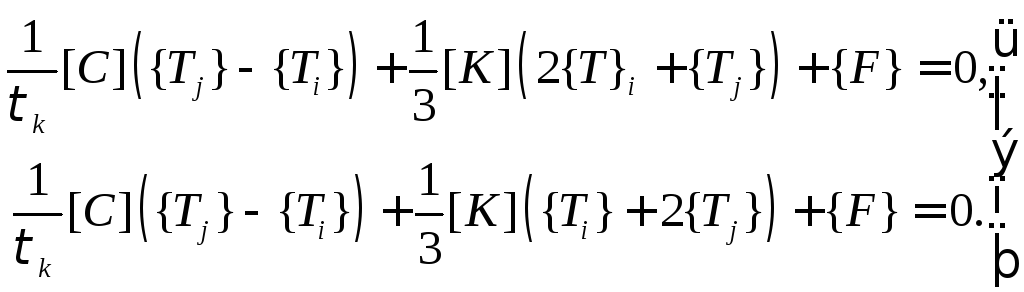
Разрешим ее относительно {}:

.

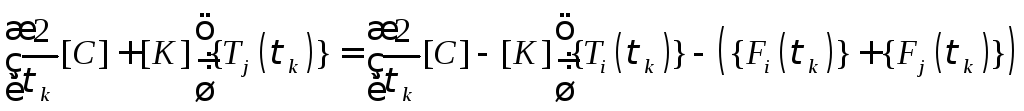Вводя обозначения:

, , (6.2.6)

последнее выражение запишем компактно:

. (6.2.7)

Уравнение (6.2.6) содержит две неизвестные – совокупности значений температур в-м и в -м узлах -го элемента. Для обеспечения непрерывности интерполяционной функции (6.2.3) в общем для соседних элементов узле должно выполняться условие:

. (6.2.8)

Подставляя (6.2.8) в (6.2.7) и опуская одинаковый для всех членов уравнения индекс , получимрекуррентное уравнение, позволяющее выразить координатные узловые значения температуры на -м временнόм шаге через совокупность их значений на предыдущем – -м шаге:

. (6.2.9)

Полученное уравнение (6.2.9) может быть решено относительно очевидно только в том случае, если известны. Именно это обусловливает обязательную последовательность данного процесса, – он должен начинаться с с последующим перебором значений . Эта процедура может быть охарактеризована какпсевдоитерационный процесс, в котором последующее значение вычисляется по найденному на предыдущем шаге. Отличие заключается в том, что значения в j-м узле находятся по значениям в i-м узле, а в итерационной процедуре значения искомой величины уточняются в одном и том же узле по найденному на предыдущем шаге в этом же узле.

На первом временнόм шаге в качестве будет фигурировать, очевидно, начальное – задаваемое – условие (6.2.2) в -м временном узле, что и позволяет найти по уравнению (6.2.9) значения температур в -м узле этого же – с – временного элемента:

. (6.2.10)

Определение по уравнению (6.2.10) и, тем самым, согласно (6.2.8) и значенийв-м узле второго временнόго элемента с , позволяет организовать последовательный процесс в соответствии с рекуррентным уравнением (6.2.9).

Таким образом, методом Галеркина система R дифференциальных уравнений решена и сведена к системе R алгебраических уравнений с числовыми коэффициентами при неизвестных значениях температуры в R глобальных координатных узлах на каждом -м временнόм элементе.

Другие способы решения системы динамических уравнений (6.2.1) описаны в [2, 6] (решение методом конечных разностей).