5.5 Естественная система координат

В случае произвольной глобальной системы координат значения узловых координат ограничены только границами области интегрирования. Было бы полезным упрощением, если бы значения этих координат были равны –1, 0, и +1. Этого можно достигнуть выбором локальной (местной) системы координат, привязанной к элементу так, чтобы координаты менялись линейно между нормированными узловыми координатами. Система координат такого типа называется системой естественных координат. Преимущество естественных координат в том, что интегрирование по элементу часто может быть проведено в стандартном аналитическом виде [1, 4, 6].

Естественные координаты могут быть, очевидно, одно- двух- и трехмерными.

В одномерном случае переход к естественной системе координат осуществляется трансляцией начала системы координат в начало отрезка . Тогда в системеимеем:

,

или, отнеся к длине отрезка:

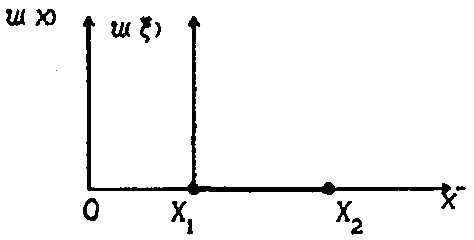
Рис. 5.1

.

Точно так же, выбирая начало в точке , найдем:.

Из выражений для нормированных координат видно, что это полиномы Лагранжа:

; . (5.4.5)

Таким образом, в одномерном случае естественные координаты – это лагранжевы, или -координаты, обладающие, как было показано ранее, всеми свойствами базисных функций. Поэтому аппроксимирующую функцию элемента можно записать в естественной системе координат так:

,

поскольку и.

Преимущество веденных -координат в том, что интегрирование можно провести аналитически согласно формуле:

, (5.4.6)

где - длина элемента.

Нормированная координата площади в двумерном случае аналогична нормированной координате длины в одномерном. Для произвольно выбранной точки в трехузельном треугольном элементе такая координата определяется делением площади треугольника А₁ (см. рис. 5.2) на площадь А всего треугольника: . Аналогично для остальных частей треугольника:

; и .

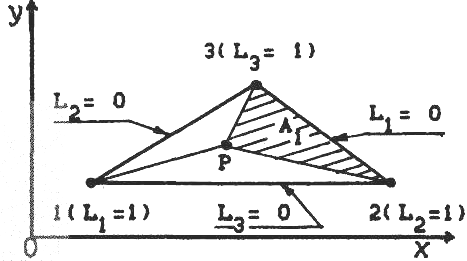
Рис. 5.2

Совмещая точку с каждым из узлов, видим, что в узлах-координаты равны 1, и равны 0 на сторонах, противоположных узлу, что и показано на рис. 5.2. Кроме того, очевидно выполнение равенства:

Отсюда следует, что из трех -координат независимыми являются толькодве любые из них, как и следовало ожидать для двумерного случая. Таким образом, введенные плоские -координаты удовлетворяют всем свойствам базисных функций элемента.

Найдем конкретное выражение для -координаты. Площадьтреугольника с вершинами,и, как известно, равна:

.

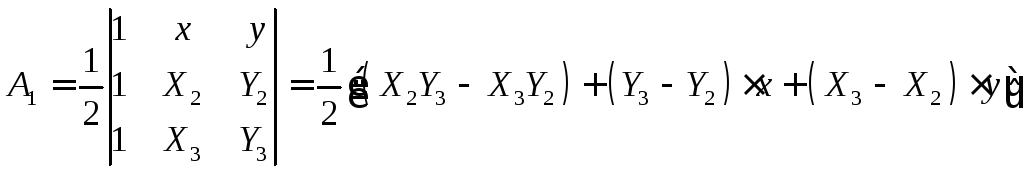Разделив на площадь треугольника, видим, чтополностью совпадает с базисной функцией, симплекс-треугольника (см. (4.1.5)). Следовательно:

; ;. (5.4.7)

Интегрирование с использованием плоских -координат осуществляется согласно формуле:

. (5.4.8)

В трехмерном случае естественными координатами служат, очевидно, отношения объемов, или объемные -координаты. Произвольно выбранной точкой тетраэдр делится на четыре подобъема. Тогда для объемной-координаты будем иметь:

.

Легко показать, что и в этом случае базисные функции равны -координатам:

; ; ; . (5.4.9)

Независимыми являются любые три из четырех объемных -координат.

Интегралы для получения стандартизованных матриц просто находить в объемных -координатах согласно формуле:

. (5.4.10)

Отметим, что в формулах интегрирования с помощью -координат (5.4.6), (5.4.8) и (5.4.10) в знаменателе стоитсумма показателей степени-координатплюс число, соответствующее размерности элемента. Это правило помогает легко запомнить формулы интегрирования.

Базисные функции элемента, или -координаты, можно использовать и для установления связи между декартовой и естественной системами координат:

x = x(ξ,η) = [L_m(ξ,η)]{X}; y = y(ξ,η) = [L_m(ξ,η)]{Y}, (5.4.11)

где {X} и {Y} – вектор-столбцы, элементами которых являются глобальные координаты (в декартовой системе) узлов элемента; индекс показывает, что базисные функции элемента использованы для преобразования координат. Например, радиус-вектор в цилиндрической системе координат можно на основании (5.4.11) представить следующим образом:

, (5.4.12)

где – радиальные координаты узлов симплекс-треугольника. Такая замена очень продуктивна при нахождении стандартизованных матриц элементов, стороны которых не совпадают с координатными линиями системы [1, 2].

При задании двух множеств узлов – одно для определения аппроксимирующей функции элемента, другое – для преобразования координат, возможны три случая:

• число узлов для определения формы элемента меньше числа узлов, использу-

емых при определении интерполяционной функции, это – субпараметрические

элементы:

• число узлов одинаковое – изопараметрические элементы;

• число узлов формы больше числа узлов полинома – это суперпараметрические

элементы. Возможность задания двух независимых множеств узлов поз­воляет сочетать как интерполяционные полиномы высокого порядка с элементами простой геометрии, так и элементы сложной формы с простыми интерполяционными полиномами [2, 6].