5.2 Матричное представление элементного вклада

Из курса матричной алгебры известно, что произведение матрицы размером (вектор-столбец) на матрицу размером(матричная строка) дает матрицу размером. Поэтому подынтегральные выражения в формуле (5.1.5) для вклада элемента сr узлами в решение задачи представляют собой матрицы размером r x r, или – как последние два члена – вектор-столбцы размером . Так как интегралы берутся в определенных размерами элемента пределах, членами проинтегрированных матриц будут – в конечном итоге – числа, независимо от того, в каком виде удается осуществить интегрирование – в аналитическом или в численном.

Каждая матрица имеет свое традиционное наименование в зависимости от физической природы решаемой задачи. Так, в задачах теплопроводности первый член в (5.1.5) называют объемной частью (интегрирование ведется по объему элемента) матрицы теплопроводности , описываемой выражением

(5.2.1):

.

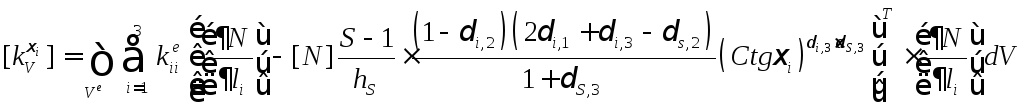Верхний индекс показывает, по какой переменной осуществляется дифференцирование базисных функций элемента. Ранг матрицы равен, где–число узлов элемента. У элементов базового каталогаr = 4÷8.

Вид производных базисных функций, полученный на основании (1.1.13) – – с учетом значений параметров Ляме в различных системах координат (см. (1.1.10)), представлен в таблице 3.

В матричном представлении первый член в (5.1.5) имеет вид:

, . (5.2.2)

В соответствии с физической природой задачи вместо берем температуру.

Число компонент объемной части матрицы теплопроводности (5.2.1) равно

трем (по числу координат) для естественно ограниченных (S=1) ограниченно симмет-

Таблица 3

Производные базисных функций

S	∂/∂li			dV
	i=1	i=2	i=3
1 2 3	∂/∂x ∂/∂r ∂/∂r	∂/∂y (1/r) ∂/∂θ (1/rSinβ) ∂/∂θ	∂/∂z ∂/∂z (1/r) ∂/∂β	dxdydz rdrdθdz r2drdθSinβdβ

ричных элементов. У полностью симметричных элементов оно сократится до двух – вследствие азимутальной симметрии-й компонент исчезнет.

Вторую матрицу в (5.1.5), также умножаемую на вектор-столбец , по аналогии называютматрицей теплопроводности элемента, но ее поверхностной частью (интегрирование ведется по поверхности -ой грани):

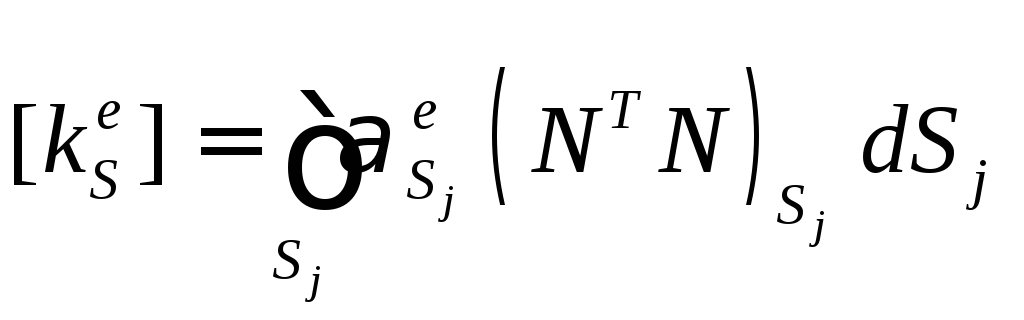, . (5.2.3)

Нижний индекс у матричного произведения базисных функций означает, что базисные функции узлов, не принадлежащих-й поверхности, должны быть заменены нулями согласно их свойству (4.5.1), а объемные (трехмерные) базисные функции принадлежащих грани узлов – преобразованы, т.е. из объемных превращены в двумерные поверхностные базисные функции, так как поверхность описывается уравнением (т.е. нормальна орту ). Очевидно, что и для разных поверхностей выражается по-разному.

Проиллюстрируем сказанное на конкретном примере. Пусть -й поверхностью является нижняя грань второго элемента каталога и ей присвоен номер 1. Она содержит узлы , и, следовательно, базисные функции остальных узлов . Уравнение плоскости, которой принадлежит первая поверхность: . Это означает, что в базисных функциях узлов этой поверхности текущую переменную нужно заменить на их-e координаты, в силу чего на основании (4.3.3) полином Лагранжа станет равным единице. Для базисной функции на этой грани будем иметь:

, , .

Вторая – верхняя грань – идентична первой, но у нее ,

, поэтому .

Остальные грани не являются в общем случае координатными плоскостями, и поэтому базисные функции их узлов нельзя преобразовать; кроме того, , что усложняет процедуру интегрирования. Число компонент объемной части матрицы теплопроводности (5.2.1) равно трем.

Базисные функции тетраэдра также, очевидно, не преобазуются в общем случае, но процедура интегрирования упро­щается переходом к естественной системе координат (см. п. 5.3).

В матричном представлении второй член в решении (5.1.5) имеет вид,

аналогичный (5.2.2):

, (5.2.4)

где - число граней элемента, на которых.

Число компонент поверхностной части матрицы теплопроводности в общем случае равно числу n граней элемента, т.е. n = 4÷6. Для удобства математического представления матрицы (5.1.2) и (5.1.4) объединяют (их ранги одинаковы), что дает:

, (5.2.5)

где – матрица теплопроводности элемента (матрица жесткости в задачах упругости).

Третий член выражения (5.1.5) принято называть матрицей демпфирования в задачах упругости, и матрицей теплоемкости в задачах теплопроводности:

. (5.2.6)

Как видно из (5.2.6), матрица [] всегда симметрична;η = c_p ρ = C_v– объемная теплоемкость материала элемента.

Физический смысл этой матрицы в обеих задачах один и тот же, – она демпфирует (уменьшает) изменения определяемой величины (в частности, температуры) и, тем самым, характеризует инерционные свойства материала элемента (следовательно, и объекта в целом).

Остальные члены, именуемые объемной и поверхностной частями вектора тепловой нагрузки (вектор нагрузки в задачах упругости), запишутся так:

; (5.2.7)

; где (5.2.8)

Процедура нахождения поверхностных частей матрицы теплопроводности (5.2.3) и вектора тепловой нагрузки (5.2.8) идентичны. Число компонент поверхностной части вектора тепловой нагрузки равно количеству граней элемента, на которых ≠ 0. В общем случае число компонент равно 4÷6.

Для удобства записи оба вектора объединяют в один вектор тепловой нагрузки:

.

Собирая все члены, получим определяющую элемент систему ( по числу

узлов элемента) обыкновенных дифференциальных уравнений первого порядка в их матричном представлении:

. (5.2.9)

Переход от частной производной по времени к обыкновенной объясняется тем, что временная производная рассматривается как функция только координат в каждый фиксированный момент времени. Стационарный случай будет описываться системойалгебраических уравнений:

. (5.2.10)