Глава 5. Вычислительные аспекты мкэ

В третьей и четвертой главах были рассмотрены первые два этапа применения МКЭ к решению краевых задач – построение сетки из конечных элементов и получение их базисных функций. В данной главе описаны и, по возможности, проиллюстрированы на конкретных примерах математические процедуры, приводящие к получению расчетных, т.е. программируемых соотношений метода.

5.1 Общее решение краевой задачи методом Галеркина

В рамках метода конечных элементов решение уравнения переноса (1.1.14) можно найти с помощью его вариационной версии или версии метода взвешенных невязок, в частности, метода Галеркина.

В первом случае требуется предварительно сконструировать функционал [2, 3, 4], обладающий экстремальными свойствами, что существенно снижает эффективность вариационного подхода. К тому же функционал, адекватный решаемой задаче, может отсутствовать вообще или не минимизировать искомую функцию в узловых точках. Отсутствие жестких правил регламентации оставляет открытым вопрос о правильности построенного функционала вплоть до стадии проверки размерности получаемых на его основе расчетных соотношений метода. Указанные недостатки наглядно проявляются при работе в системе координат с порядком симметрии [1, 14].

Отсутствие процедуры формирования функционала и использование непосредственно дифференциального уравнения делает методы взвешенных невязок более предпочтительными, особенно если учесть возможность получения с их помощью решения, содержащего варьируемый параметр , т.е. найти общее решение уравнения, справедливое в любой системе координат. 0бщее решение задачи получим с помощью метода Галеркина, для чего достаточно, как указывалось в п. 2.2, найти его для отдельного элемента (см. (2.2.2)).

Уравнение переноса (1.1.14) и граничное условие (1.2.7) к нему должны быть записаны для произвольного элемента, что легко достигается приписыванием всем входящим в них функциям и параметрам индекса , указывающего номер элемента. Запишем аппроксимирующую функцию элемента в более удобной матричной форме:

, , (5.1.1)

где [] – матричная строка размером, элементами которой являются базисные функции в узлах элемента;{(ζ_i)}−вектор-столбец размером значений искомой функции в узлах элемента;− число принадлежащих элементу узлов,ξ_i , ζ_i – текущие переменные и координаты узлов, соответственно (i=1,2,3). В дальнейших выкладках для краткости записи индекс e опускаем.

Согласно методу Галеркина приближенное решение уравнения переноса (1.1.14) для элемента в общем виде будет описываться выражением (2.2.2), в которое внесен дифференциальный оператор (1.1.14):

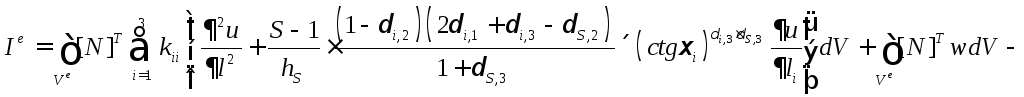
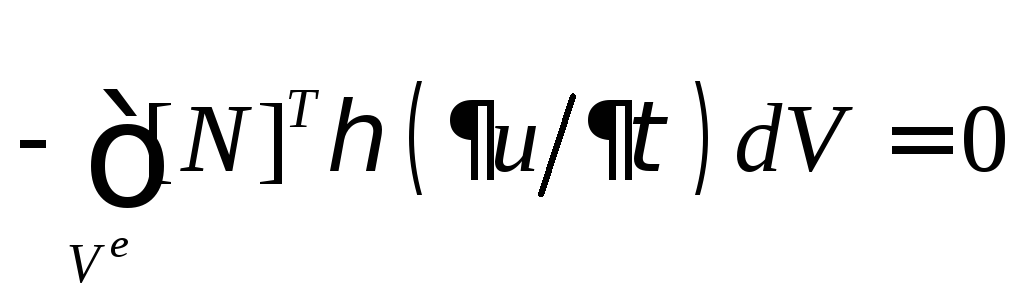, (5.1.2)

где – вектор-столбец базисных функций для элемента сузлами.

Соотношение (5.1.2) содержит дифференциальный оператор 2-го порядка, что не позволяет использовать линейные базисные функции, математически описывающие элементы базового каталога. С целью понижения порядка оператора выразим вторую производную функции по обобщенной переменнойследующим образом:

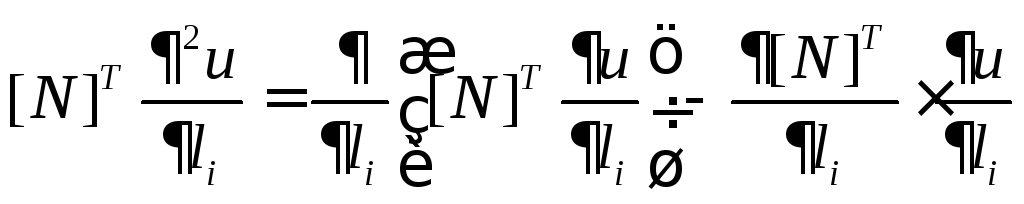. (5.1.3)

Первое слагаемое в (5.1.2) на основании (5.1.3) представим в виде:

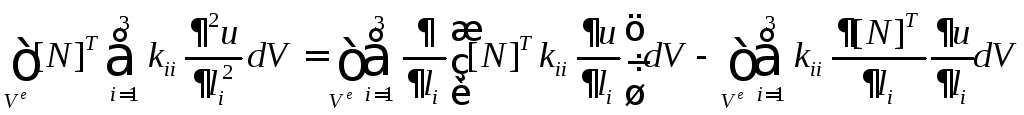. (5.1.4)

Воспользовавшись теоремой Остроградского-Гаусса, заменим в (5.1.4) первый интеграл по объему интегралом по поверхности,охватывающей объем элемента:

.

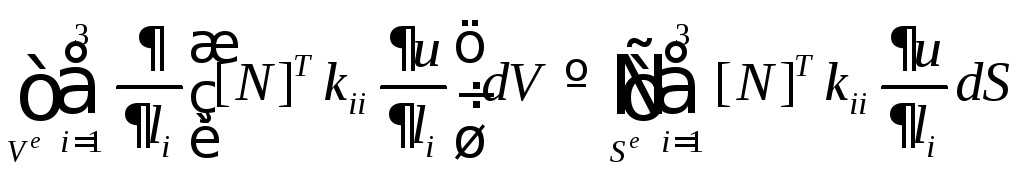Подинтегральное выражение в поверхностном интеграле выразим из предварительно умноженного на граничного условия (1.2.7):

.

Используя версию МКЭ (5.1.1), можем написать:

; .

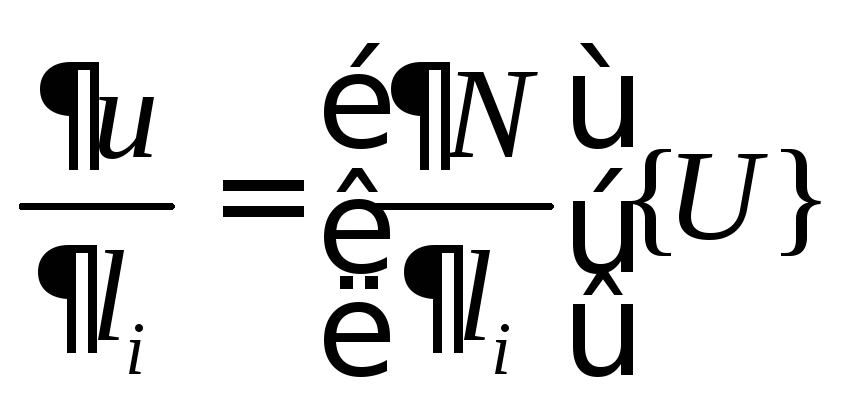Подставляя полученные путем указанных преобразований результаты в уравнение (5.1.2), решение задачи для элемента e запишем в общем виде:

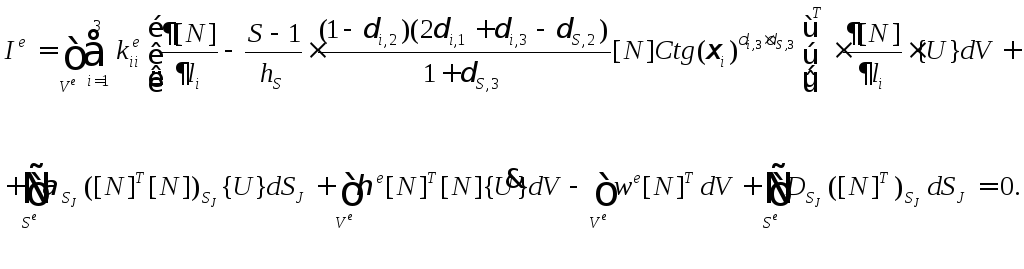
(5.1.5)

, .

Найденное методом Галеркина общее решение (5.1.5) справедливо для элемента любой размерности и геометриис произвольнымr числом узлов. При вариационном же подходе функционал необходимо конструировать для каждой из систем координат отдельно.

Решение для всей области определения получается суммированием по всем E-элементам элементных вкладов: .