
- •А.В. Румянцев
- •Содержание
- •Глава 6. Программная реализация метода
- •Глава 1. Краевые задачи теории поля
- •1.1 Уравнение переноса в обобщенной криволинейной системе координат
- •1.2 Краевые условия задачи
- •1.3* Краткая характеристика методов решения краевой задачи
- •Глава 2. Метод конечных элементов в краевых
- •2.1 Методы взвешенных невязок
- •2.2 Основная концепция метода конечных элементов
- •Глава 3. Геометрические аспекты мкэ
- •3.1 Типы конечных элементов. Базовый каталог элементов
- •3.2 Дискретизация области на элементы
- •А) с разными (вид сверху); б) с одинаковыми.
- •Цифры – это номер элемента по каталогу
- •3.3 Нумерация элементов и узлов
- •3.4 Индексация узлов и формирование таблицы входных данных
- •Осесимметричной детали
- •Геометрическая часть таблицы входных данных
- •Глава 4. Математическое описание элемента
- •4.1 Метод Крамера
- •4.2 Метод Лагранжа
- •4.3 Обобщенный метод Крамера-Лагранжа
- •4.4 Эрмитовы элементы
- •4.5 Свойства базисных функций элемента
- •Глава 5. Вычислительные аспекты мкэ
- •5.2 Матричное представление элементного вклада
- •Производные базисных функций
- •5.3 Формирование глобальных матриц для исследуемой области
- •А) Сокращенная
- •5.4 Стандартизация матриц элементов
- •5.5 Естественная система координат
- •5.6 Средние температуры элемента
- •Глава 6. Программная реализация мкэ
- •6.1 Задание краевых условий задачи
- •6.2 Решение системы динамических уравнений
- •Временная циклограмма q(τ)
- •6.З Учет температурной зависимости теплофизических параметров
- •6.4 Радиационный компонент теплообмена
- •6.5 Сходимость, полнота и согласованность, точность
- •Базовый каталог объемных элементов
- •Осесимметричные объемные элементы
- •Базовый каталог одно- и двумерных элементов
4.2 Метод Лагранжа
Достоинство
первого способа состоит в его применимости
к любым элементам независимо от их
размерности и количества узлов. С его
помощью при известном в явном виде
аппроксимирующем полиноме
![]() -го
ранга базисные функции в принципе
всегда могут быть найдены, так как
матрица типа (4.1.2) обратима, поскольку
ее определитель (4.1.3) отличен от нуля,
– площадь или объем элемента никогда
не равны нулю. Универсальность метода
Крамера нивелируется его неэффективностью
при числе узлов элемента
-го
ранга базисные функции в принципе
всегда могут быть найдены, так как
матрица типа (4.1.2) обратима, поскольку
ее определитель (4.1.3) отличен от нуля,
– площадь или объем элемента никогда
не равны нулю. Универсальность метода
Крамера нивелируется его неэффективностью
при числе узлов элемента![]() .
.
К элементам, образованным координатными линиями, целесообразно применять более простой метод Лагранжа.
Рассмотрим
аппроксимацию функции
![]() полиномом
полиномом![]() -го
ранга, считая, что значения функции
заданы как
-го
ранга, считая, что значения функции
заданы как![]() в
в![]() точках
точках![]() .
Из численного анализа известно, что
функция
.
Из численного анализа известно, что
функция
![]() может быть задана как полином
может быть задана как полином
![]() -ой
степени:
-ой
степени:
![]() ,
(4.2.1)
,
(4.2.1)
где
![]() – полином Лагранжа, определяемый
равенством:
– полином Лагранжа, определяемый
равенством:
![]() .
(4.2.2)
.
(4.2.2)
Если
под
![]() понимать аппроксимирующую элементную
функцию
понимать аппроксимирующую элементную
функцию
![]() ,
то из сопоставления (4.2.1) с (2.2.1) видно,
что полиномы
Лагранжа – это базисные функции
элемента, а базовые точки
,
то из сопоставления (4.2.1) с (2.2.1) видно,
что полиномы
Лагранжа – это базисные функции
элемента, а базовые точки
![]() –координаты
его узлов,
или узловые точки.
–координаты
его узлов,
или узловые точки.
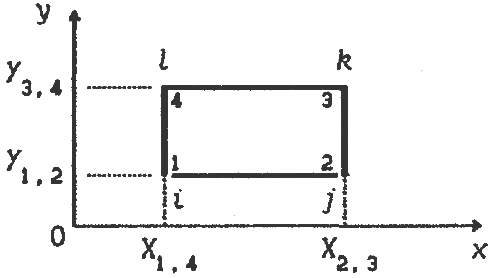
Проиллюстрируем метод Лагранжа на примере изображенного на рис. 4.4 элемента, образованного координатными линиями декартовой системы [4].
Использование равенств (4.2.1) и (4.2.2) на стороне 1–2 (y=const), позволяет определить u(x) на этой стороне:
![]() ,
,
где
![]() ;
;![]() ;
;
Аналогично
на стороне 4–3
![]() получим:
получим:
![]() .
.
Применяя
эти же рассуждения для сторон с
![]() ,
найдем:
,
найдем:
![]() ,
где
,
где
![]() ;
;![]() .
.
Собирая полученные выражения, для аппроксимирующей функции элемента будем иметь:
![]()
Видно, что попарные произведения полиномов Лагранжа соответствуют базисным функциям элемента:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Здесь
![]() – площадь элемента.
– площадь элемента.
Обобщая
эти соотношения на трехмерный элемент
– координатную ячейку, придем к его
математическому описанию в виде
произведения трех лагранжевых полиномов,
справедливому при любом
![]() :
:
![]() ,
p
≠ q,
(4.2.4)
,
p
≠ q,
(4.2.4)
где
ξi
– текущая переменная; ζi
–
координаты q-го
и p-го
узлов; p
–
индексы узлов, с которыми узел q
расположен на координатных поверхностях
![]() .
.
Как следует из (4.2.4), методом Лагранжа легко получить базисные функции всех элементов каталога, кроме второго, шестого и седьмого.
4.3 Обобщенный метод Крамера-Лагранжа
Особенность
2-го, 6-го и 7-го элементов в том, что они
лишь частично образуются координатными
поверхностями системы. Поскольку число
их узлов
![]() ,
применять к ним универсальный метод
Крамера нецелесообразно. Возможен
другой, более эффективный способ,
сочетающий методы Крамера и Лагранжа.
,
применять к ним универсальный метод
Крамера нецелесообразно. Возможен
другой, более эффективный способ,
сочетающий методы Крамера и Лагранжа.
Введем
иерархию
элементов, подразделив их на порождающие
с
![]() ,
ипорождаемые
с
,
ипорождаемые
с
![]() .
Порождение элемента можно осуществитьтрансляцией
порождающего
элемента в общем случае в произвольном
направлении, или его поворотом
вокруг
некоторой оси на угол
.
Порождение элемента можно осуществитьтрансляцией
порождающего
элемента в общем случае в произвольном
направлении, или его поворотом
вокруг
некоторой оси на угол
![]() –
дляограниченно
симметричных, или на
–
дляограниченно
симметричных, или на
![]() – дляосесимметричных
элементов. В результате размерность
порожденного элемента увеличится на
единицу.
– дляосесимметричных
элементов. В результате размерность
порожденного элемента увеличится на
единицу.
Так
как порождающий элемент не образован
координатными поверхностями, то его
базисные функции находятся методом
Крамера при
![]() ,
а затем к нему применяется метод
Лагранжа, который равнозначен операциям
трансляции или поворота. В силу этого,
достаточнобазисные
функции
порождающего двумерного
элемента умножить
на полином
Лагранжа
,
а затем к нему применяется метод
Лагранжа, который равнозначен операциям
трансляции или поворота. В силу этого,
достаточнобазисные
функции
порождающего двумерного
элемента умножить
на полином
Лагранжа
![]() в
направлении орта
трансляции, чтобы получить базисные
функции порожденного объемного элемента
в
направлении орта
трансляции, чтобы получить базисные
функции порожденного объемного элемента
![]() :
:
![]() ,
,
![]()
![]() .
(4.3.1)
.
(4.3.1)
Применяя обобщенный метод Крамера-Лагранжа ко второму элементу каталога, для его базисных функций получим следующее выражение:
![]() ,
при
,
при
![]()
![]() (4.3.2)
(4.3.2)
где
![]() – базисные функции (4.1.7) треугольного
элемента; а полиномы Лагранжа равны:
– базисные функции (4.1.7) треугольного
элемента; а полиномы Лагранжа равны:
![]() ;
;
![]() .
(4.3.3)
.
(4.3.3)
Эти же формулы описывают и седьмой элемент базового каталога, если в
базисных
функциях переменные![]() заменить
на
заменить
на
![]() ,
а в полиноме Лагранжа –
,
а в полиноме Лагранжа –![]() на
на![]() :
:
![]() .
(4.3.4)
.
(4.3.4)
У
шестого элемента на полиномы Лагранжа
![]() умножаются лишь базисные функции узлов
умножаются лишь базисные функции узлов![]() и
и![]() .
.
Все
полностью симметричные элементы
базового каталога относятся к порожденным
поворотом на
![]() порождающих их двумерных элементов. В
силу того, что при этом
порождающих их двумерных элементов. В
силу того, что при этом![]() ,
базисные функции порожденных и
порождающих их элементов идентичны.
,
базисные функции порожденных и
порождающих их элементов идентичны.
