3.3 Нумерация элементов и узлов

Элементы, на которые разбита конструкция, необходимо индивидуализировать, что проще всего достигается присвоением ему номера . Он никак не связан с номеромэлемента по каталогу, фиксирующим его геометрию. Нумерация элементов не влияет на вычислительные аспекты МКЭ и поэтому представляет собой простую процедуру, опирающуюся на естественное пожелание удобства при пользовании. Очевидно, что элементы, относящиеся к частям конструкции при укрупненном ее расчленении, должны

иметь последовательную нумерацию. Номер элемента будем заключать в круглые скобки – – во избежание путаницы с номером(по каталогу) и с номерами узлов.

Нумерация узлов существенно влияет на эффективность вычислений. Применение МКЭ к решению дифференциального уравнения приводит к системе алгебраических уравнений (необязательно линейных), большое число коэффициентов в которой равно нулю. Все ненулевые коэффициенты (и некоторые нулевые) в глобальной матрице коэффициентов находятся между двумя линиями, параллельными главной диагонали. Расстояние между главной диагональю и этими линиями называется шириной полосы матрицы. Все коэффициенты вне этой полосы равны нулю, и они не заносятся в память ЭВМ (это одно из преимуществ МКЭ). Уменьшение ширины полосы приводит к уменьшению требуемого объема памяти и к сокращению времени вычислений.

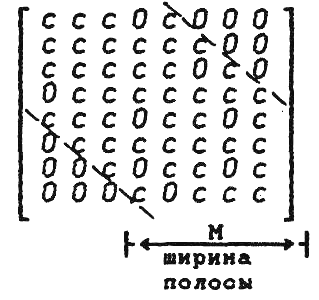
В конкретных расчетах структура

матрицы может быть представлена набором целочисленных пар , каждая из которых означает пару переменных (т.е. номера строки и столбца). Полуширина М матрицы определя-

ется при этом максимумом величины , взятой по всем-элементам матрицы [3]:

. (3.3.1)

При работе с векторными величинами (например, скорость или перемещение в узле), величину нужно умножить на числонеизвестных в узле (число компонент векторной величины). В общем случае:

. (3.3.2)

Для скалярной величины, такой как температура, очевидно, .

Объем памяти, необходимой для профильной записи матрицы, определяется формулой:

. (З.3.3)

Правильной нумерацией узлов, очевидно, будет та, которая минимизирует либо полуширину , либо профиль, в зависимости от предполагаемой формы

записи. В большинстве случаев минимизация минимизирует и.

На рис. 3.4 представлены различные варианты нумерации узлов (и элементов). Сопоставление получаемых показывает предпочтительность последнего варианта, в котором обеспечивается наименьшая из максимальных разница между номерами узлов, принадлежащих одному элементу. Это достигается последовательной нумерацией узлов при движении в направлениинаименьшего размера тела. Если от четырехугольных элементов перейти к треугольным, то при правильной нумерации меньшие получаются при проведении левой диагонали, как показано на рис. 3.3. Переход к треугольным элементам лишь удваивает число элементов, не

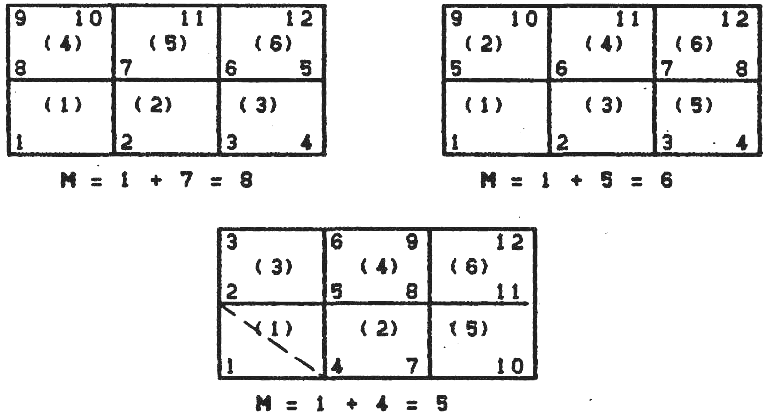
Рис. 3.4 К вопросу нумерации узлов

сказываясь на количестве узлов. Как уже указывалось, нумерация элементов носит произвольный характер, так как формирование глобальных матриц из матриц элементов осуществляется по номерам узлов, а не элементов.