
Sluchaynye_protsessy
.pdfМинистерство образования Республики Беларусь
Учреждение образования БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИНФОРМАТИКИ И
РАДИОЭЛЕКТРОНИКИ
_______________________________________________________________
Кафедра информационных технологий автоматизированных систем
В. С. Муха
Случайные процессы
Минск 2011
УДК 519.72 (075.8) ББК 22.172 я 73
М 92
Рецензент: профессор кафедры высшей математики БГУИР, кандидат физико- математических наук А.А. Карпук
Муха В.С.
М 92 Случайные процессы: Учеб. пособие / В.С. Муха. – Мн.: БГУИР, 2011. – 81 с.: ил.
ISBN-985-444-581-Х
В учебном пособии излагаются основы теории случайных процессов. Приводятся сведения из теории множеств, рассматриваются некоторые вопросы теории вероятностей. Даются основные определения теории случайных процессов. Рассматриваются различные классы случайных процессов с непрерывным и дискретным временем, непрерывными и дис- кретными значениями (состояниями). Изучаются свойства выборочных функций и динамические преобразования случайных процессов.
Пособие рассчитано на студентов технических специальностей выс- ших учебных заведений.
УДК 519.72 (075.8) ББК 22.172 я 73
М 92
ISBN-985-444-581-Х |
© Муха В.С., 2011 |
|
© БГУИР, 2011 |
2
ПРЕДИСЛОВИЕ
Вучебном пособии излагаются основы теории случайных процессов. Предполагается, что читатель изучил теорию вероятностей в определенном объеме и на определенном уровне.
Первый раздела пособия под названием «Некоторые вопросы теории вероятностей» пред- ставляют собой своего рода «философские тетради» автора в области теории вероятностей. Они могут быть полезны тем, кто пожелает повторно пробежаться по теории вероятностей для восстановления знаний в этой области, возможно, не некотором более высоком уровне.
Выбор тем для рассмотрения отражает предпочтения автора. Например, в пособии не рас- сматриваются случайные последовательности типа авторегрессии–скользящего среднего и подобные им ввиду того, что теория этих процессов, по мнению автора, не имеет преиму- ществ перед корреляционной теорией случайных процессов.
Впособии представлен достаточно широкий набор классов случайных процессов: с не- прерывным и дискретным временем, с непрерывными и дискретными состояниями, стацио- нарные случайные процессы, марковские случайные процессы. Изучаются свойства выбо- рочных функций и динамические преобразования случайных процессов. Эта коллекция во-
просов представляется изначально необходимой для возможности совершения дальнейшего путешествия в область случайных процессов.
При изложении материала автор исходил из того, что при изучении дисциплины подле- жит усваиванию не только набор фактов и теоретических положений, но и доказательный инструментарий дисциплины. Поэтому изложение сопровождается доказательствами. Одна- ко в случаях, когда существующие доказательства, по мнению автора, оказывались громозд- кими или выходящими по сложности за определенный уровень знаний, предпочтение отда- валось изложению только фактического материала.
При написании пособия использовались литературные источники, приведенные в списке литературы. Однако конкретные ссылки по отдельным вопросам в пособии не приводятся.
Пособие предназначено для студентов технических специальностей высших учебных за- ведений. Оно может быть полезным также магистрантам, аспирантом и преподавателям.
3

1.НЕКОТОРЫЕ ВОПРОСЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
1.1.Операции над множествами
Воснове теории вероятностей и, как следствие, теории случайных процессов лежит тео- рия множеств. Приведем некоторые сведения из теории множеств и теории вероятностей, на которые нам придется в дальнейшем опираться. При изложении материала будем исходить из того, что читатель изучал курс теории вероятностей в том или ином объеме с той или иной степенью строгости, например, в рамках учебного пособия [9].
Пусть A, B , C , …, Ai , i =1,2,..., – произвольные множества. Объединением множеств Ai называется множество B , каждый элемент которого x B принадлежит хотя бы одному их множеств Ai (рис 1.1). Обозначается объединение следующим образом:
B = U Ai = A1U A2 U... .
i
Рис. 1.1. Объединение множеств
Пересечением множеств Ai называется множество B , каждый элемент которого x B принадлежат каждому из множеств Ai , i =1,2,... (рис 1.2). Обозначается пересечение сле-
дующим образом:
B = I Ai = A1I A2 I... .
i
Рис. 1.2. Пересечение множеств
4

Операции объединения и пересечения по своему определению коммутативны, т.е.
A1U A2 = A2 U A1 , A1I A2 = A2 I A1 ,
и ассоциативны:
(AU B)UC = A(BUC),
(AI B)IC = AI(BIC).
Кроме того, они взаимно дистрибутивны:
(AU B)IC = (AIC)U(BIC),
(AI B)UC = (AUC)I(BUC).
Разностью множеств A и B называется множество C = A \ B , каждый элемент которого x C принадлежит A и не принадлежит B (рис. 1.3).
Рис. 1.3. Разность множеств A и B
Симметрической разностью множеств A и B называется объединение разностей множе- ство A \ B и B \ A (рис. 1.4). Обозначается симметрическая разность как A B и по опре-
делению равна
C = A B = (A \ B)U(B \ A).
Рис. 1.4. Симметрическая разность множеств A и B
5

В теории вероятностей рассматриваются не произвольные множества, а подмножества не- которого основного множества Ω, Ai Ω . В этом случае множество C = Ω \ A называет-
ся дополнением множества A (до множества Ω) и обозначается как A , так что A = Ω \ A.
Рис. 1.5. Дополнение множества A до Ω
Для подмножеств некоторого множества Ω важную роль играет так называемый принцип двойственности, определяемый следующими двумя соотношениями:
1. Дополнение объединения равно пересечению дополнений
|
= I |
|
. |
|
U Ai |
Ai |
(1.1) |
||
i |
i |
|
||
2. Дополнение пересечения равно объединению дополнений
I Ai = U Ai .
i i
Смысл принципа двойственности состоит в том, что из любой теоремы, относящейся к под- множествам фиксированного множества Ω, автоматически может быть получена другая – двойственная – теорема путем замены в исходной теореме всех рассматриваемых множеств их дополнениями, объединений – пересечениями, а пересечений – объединениями.
Приведем доказательство равенства (1.1). Пусть X = U Ai . Это означает, что x не явля-
|
|
i |
|
|
|
||
|
|
, а потому x I |
|
. Пусть теперь |
x I |
|
, |
ется элементом ни одного из дополнений |
Ai |
Ai |
Ai |
||||
|
|
i |
i |
||||
т.е. является элементом каждого из множеств Ai . Тогда x не является элементом ни одного
из Ai и их объединения U Ai . Значит, |
x является элементом дополнения |
U Ai |
. Равенство |
i |
|
i |
|
(1.1) доказано. Аналогично доказывается равенство (1.2), а также другие равенства, относя- щиеся к множествам.
1.2. Мощность множества
Два множества A и B называются эквивалентными, если между их элементами можно установить взаимно-однозначное соответствие.
Множество называется конечным, если содержит конечное число элементов. В противном случае оно называется бесконечным. Простейшим из бесконечных множеств является счет- ное множество. Множество называется счетным, если его элементам можно поставить в со-
6
ответствие элементы множество натуральных чисел N = {1,2,...}, иначе говоря, можно про-
нумеровать натуральными числами.
Для характеристики количества элементов множества применяется понятие мощности множества. Мощность конечного множества определяется как количество его элементов. Счетное множество имеет бесконечную мощность. Существуют множества с большей чем счетное множество мощностью. Такие множества называются несчетными. Примером не- счетного множества является отрезок [0,1] действительной прямой. Говорят, что множество
[0,1], а также любое эквивалентное ему множество, имеет мощность континуума. Любое та- кое множество называется континуумом. Континуумом является, помимо отрезка [0,1], вся действительная прямая, а также любой промежуток действительной прямой.
1.3. Упорядоченные множества. Точная верхняя грань множества
Множество M называется упорядоченным, в нем задано отношение порядка, т.е. прави- ло, позволяющее установить, какой элемент за каким следует. В упорядоченном множестве для двух его элементов a,b M имеет смысл запись вида a ≤ b , что означает, что элемент
a предшествует элементу b, или что a не больше b. Примером упорядоченного множества является множество действительных чисел R с естественным порядком чисел в нем.
Пусть A – подмножество упорядоченного множества Ω. Верхней гранью подмножества A Ω называется такой элемент b Ω , что любой элемент a A не превосходит b Ω , a ≤ b . Если множество верхних граней подмножества A имеет наименьший элемент c , то c называется точной верхней гранью подмножества A Ω и обозначается sup A или
sup a (от латинского supremum – наивысшее). Аналогично точная нижняя грань подмноже- aΩ
ства A Ω – наибольший из элементов a Ω , за которым следуют все элементы A. Точ-
ная нижняя грань обозначается как inf A или inf a (от латинского infimum – наинизшее). |
|
aΩ |
|
Если точная верхняя грань подмножества A Ω принадлежит |
A, то она называется |
максимумом подмножества A и обозначается max A или max a . |
Если точная нижняя |
a A |
|
грань подмножества A Ω принадлежит A, то она называется минимумом подмножества
A и обозначается min A или min a . a A
1.4. Системы множеств
Системой множеств или множеством множеств называется множество, элементы которо- го сами являются какими-либо множествами. Для теории вероятностей важны системы мно- жеств, каждое из которых является подмножеством некоторого фиксированного множества
Ω.
Итак, пусть Ω – произвольное множество. Непустая система U некоторых его подмно-
жеств A Ω , B Ω , … называется кольцом множеств, если объединение и разность лю- бых двух множеств этой системы также принадлежат этой системе, т.е. для любых A U и B U выполняются условия
AU B U , A \ B U .
Иначе говоря, кольцо – это система множеств, замкнутая относительно операций объедине- ния и разности двух множеств. Легко показать, что кольцо – это система множеств, замкну-
7
тая также относительно операции пересечения любых двух множеств. Для этого достаточно воспользоваться очевидной из рис. 1.2 формулой
AI B = A \ (A \ B) .
Если A U , B U , то по определению кольца A \ B U , A \ (A \ B) U , следовательно и AI B U , что требовалось доказать. Таким образом, кольцо является системой, замкну-
той относительно любой операции над двумя множествами системы, т.е. в результате вы- полнения любых операций над двумя множествами системы мы получим множества, не вы- ходящие из этой системы. По индукции легко показать, что кольцо – это система, замкнутая относительно операций объединения и пересечения любого конечного числа множеств. Это значит. что если Ai U , i =1,2,...,n , то и
n |
n |
U Ai U , I Ai U . |
|
i =1 |
i =1 |
Если кольцо подмножеств Ai Ω включает и Ω, то такая система называется алгеброй множеств.
Пример 1.1. Для любого непустого множества Ω система U = {Ο/,Ω}, состоящая из пус-
того множества Ο/ и самого Ω, является алгеброй множеств. В самом деле,
ΩUΟ/ = Ω U , Ω \ Ο/ = Ω U , Ω U .
Пример 1.2. Система всех промежутков действительной прямой вида [a,b) и конечных
объединений таких непересекающихся промежутков является кольцом.
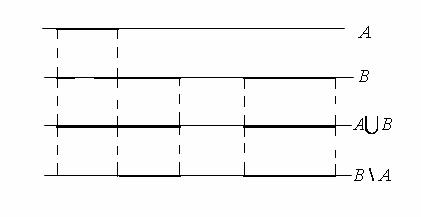
На рис. 1.6 изображены два подмножества A и B действительной прямой, представляю- щие собой конечные объединения непересекающихся промежутков вида [a,b) , а также их
объединение AU B и разность B \ A. Видно, что множества AU B и B \ A также пред- ставляют собой конечные объединения непересекающихся промежутков вида [a,b) . Следо- вательно, определенная в примере 1.2 система множеств образует кольцо множеств. Эта сис- тема будет алгеброй, если допустить a = −∞ , b = ∞ .
Рис. 1.6. Кольцо и алгебра множеств на действительной прямой
В ряде случаев приходится рассматривать объединения и пересечения не только конечно- го, но и счетного числа множеств. В этих случаях мы приходим к понятиям σ -кольца и σ - алгебры множеств (сигма-кольца и сигма алгебры).
Непустая система F подмножеств Ai Ω некоторого множества Ω называется σ - кольцом, если из того, что Ai F , i =1,2,... , следует, что
8

∞
U Ai F ,. Ai \ Aj F . i =1
Можно показать, что σ -кольцо замкнуто также относительно операции пересечения счетно- го количества множеств, т.е.
∞
IAi F .
i=1
Сигма-кольцо, включающее Ω, называется σ -алгеброй множеств Ai Ω .
Понятно, что σ -кольцо и σ -алгебра определяются для бесконечного множества Ω. Пример 1.3. Совокупность всех подмножеств бесконечного множества Ω является σ -
алгеброй.
Сигма-алгебра может быть построена на основе произвольно выбранной системы под- множеств некоторого множества. Подтверждается это следующей теоремой.
Теорема 1.1 (о минимальной σ -алгебре над системой множеств). Для любой непустой системы множеств U существует σ -алгебра σ(U ), содержащая U и содержащаяся в лю-
бой σ -алгебре, содержащей U . Эта σ -алгебра σ(U ) называется минимальной над систе- мой U .
Доказательство. Рассмотрим объединение всех множеств Ai Ω , входящих в исход-
ную систему множеств U ,
X = U Ai .
Ai U
Совокупность всех подмножеств множества X является, как известно, σ -алгеброй (см. пример 1.3). Обозначим ее σ(X ) . Пусть V – совокупность всех σ -алгебр Ri , содержащих-
ся в σ(X ) |
и содержащих U . Пересечение |
IRi и будет искомой σ -алгеброй σ(U ). До- |
|
Ri V |
|
казательство закончено. |
произвольной системы множеств U |
|
Теорема |
1.1 позволяет множества |
|
(U = {Ai Ω, i = 1,2,...}) считать элементами σ -алгебры σ(U ).
В теории вероятностей рассматривается так называемая σ -алгебра борелевских множеств (борелевская σ -алгебра). Сигма-алгеброй борелевских множеств на действительной прямой называется минимальная сигма-алгебра над системой всех полуоткрытых промежутков (на- пример, промежутков вида [a,b) ). Борелевскую σ -алгебру, грубо говоря, можно себе пред-
ставить как совокупность множеств, полученных из указанных промежутков с помощью счетного числа операций объединения, пересечения и взятия разностей. Это весьма богатый класс множеств, заведомо достаточный для практических целей. Например, наряду с проме- жутками [a,b) он содержит также одноточечные множества {a} и множества [a,b] , (a,b],
(a,b) ( a и b могут принимать также бесконечные значения). Элементы борелевской σ - алгебры называются борелевскими множествами.
Вn -мерном действительном пространстве Rn , элементами которого являются точки
x= (x1, x2 ,...,xn ) , также можно рассматривать борелевскую σ -алгебру. Множество точек
(x , x |
2 |
,..., x |
n |
) в Rn |
, координаты которых удовлетворяют неравенствам a |
j |
≤ x |
j |
< b |
j |
, |
1 |
|
|
|
|
|
|
j =1,n , называется полуоткрытым интервалом в Rn . Сигма-алгебра, минимальная над сис-
темой всех полуоткрытых интервалов в Rn , называется борелевской σ -алгеброй в Rn .
9

Иногда приходится рассматривать бесконечномерное действительное пространство R∞ , которое является множеством точек с бесконечным числом координат x = (x1, x2 ,...). Полу-
открытый интервал в R∞ представляет собой множество точек x = (x1, x2 ,...), координаты которых удовлетворяют конечному числу неравенств a j ≤ x j < bj , j =1,n . Как и раньше,
борелевской σ -алгеброй в R∞ является σ -алгебра, минимальная над указанными интерва- лами.
10
