
- •Введение в численные методы
- •3.Численные методы
- •Глава 1. Ошибки вычислений
- •Глава 3. Аппроксимация функций
- •Глава 4. Численное дифференцирование
- •Глава 5. Численное интегрирование
- •Глава 6. Численное решение нелинейных уравнений
- •6.5.Метод Ньютона
- •Глава 7. Численное решение систем нелинейных уравнений
- •Глава 8. Численное решение обыкновенных дифференциальных уравнений
- •Глава 9. Численные методы решения экстремальных задач
ВВЕДЕНИЕ В ЧИСЛЕННЫЕ МЕТОДЫ
1.Математическое моделирование и использование ЭВМ в решении прикладных задач.
В современной науке и технике важную роль играет математическое моделирование, заменяющее эксперименты с реальными объектами экспериментами с их математическими моделями.
Математические модели являются одним из основных инструментов познания человеком явлений окружающего мира. Под математическими моделями понимают основные закономерности и связи, присущие изучаемому явлению. Это могут быть формулы или уравнения, наборы правил или соглашений, выраженные в математической форме. Испокон веков в математике, механике, физике и других точных науках естествознания для описания изучаемых ими явлений использовались математические модели. Так, законы Ньютона полностью определяют закономерности движения планет вокруг Солнца. Используя основные законы механики, относительно нетрудно составить уравнения, описывающие движение космического аппарата, например, от Земли к Луне. Однако получить их решение в виде простых формул не представляется возможным.
Применение компьютеров для математического моделирования изменило само понятие "решить задачу". До этого исследователь удовлетворялся написанием математической модели. А если ему еще удавалось доказать, что решение (алгоритм) в принципе существует, то этого было достаточно, если априори полагать, что модель адекватно описывает изучаемое явление. Поскольку, как правило, нет простых формул, описывающих поведение модели, а, стало быть, и объекта, который описывается моделью, то единственный путь – свести дело к вычислениям, применению численных методов решения задач.
В настоящее время выработалась технология исследования сложных проблем, основанная на построении и анализе с помощью ЭВМ математических моделей изучаемого объекта. Такой метод исследования называют вычислительным экспериментом.
Математическое моделирование и вычислительный эксперимент применяются сегодня не только в точных науках и технике, но и в экономических науках, социологии и многих других областях, традиционно считавшихся далекими от математики и компьютеров. Зачем нужен вычислительный эксперимент? Проектирование сложных объектов, например, атомных, космических и многих других требует проведения колоссальных объемов вычислений. Например, для решения многих прикладных задач аэродинамики и ядерной физики требуется выполнения
более арифметических операций. Современные технологии зачастую используют предельные режимы, которые требуют учета сложных нелинейных факторов. Зачастую требуется изучить поведение объекта в
1
экстремальных и аварийных ситуациях, что практически невозможно путем натурного эксперимента, например, при изучении ядерных взрывов, последствий техногенных катастроф и во многих других ситуациях.
2. Вычислительный эксперимент и его этапы.
Широкое применение ЭВМ в математическом моделировании, достаточно мощная теоретическая и экспериментальная база позволяют говорить о вычислительном эксперименте как о новой технологии и методологии в научных и прикладных исследованиях.
Вычислительный эксперимент – это эксперимент над математической моделью объекта на ЭВМ, который состоит в том, что по одним параметрам модели вычисляются другие её параметры и на этой основе делаются выводы о свойствах явления, описываемого математической моделью.
В проведении вычислительного эксперимента участвует коллектив исследователей - специалисты в конкретной предметной области, математики теоретики, вычислители, прикладники, программисты. Это
связано с тем, |
что моделирование реальных объектов на ЭВМ включает в |
|
себя большой |
объём |
работ по исследованию их физической и |
математической |
моделей, |
вычислительных алгоритмов, программированию |
и обработке результатов. Здесь можно заметить аналогию с работами по
проведению |
натурных |
экспериментов: |
составление |
программы |
экспериментов, |
создание |
экспериментальной |
установки, |
выполнение |
контрольных экспериментов, проведение серийных опытов, обработки экспериментальных данных и их интерпретация и т.д. Таким образом, проведение крупных комплексных расчётов следует рассматривать как эксперимент, проводимый на ЭВМ или вычислительный эксперимент.
Вычислительный |
эксперимент играет |
ту |
же |
роль, |
что |
и |
|||||
обыкновенный |
эксперимент |
при |
исследованиях |
новых |
гипотез. |
||||||
Современная |
гипотеза |
почти всегда |
имеет математическое |
описание, |
над |
||||||
которым |
можно |
выполнять эксперименты. |
|
|
|
|
|
||||
При |
введении этого понятия |
следует |
особо |
выделить способность |
|||||||
компьютера |
выполнять большой |
объем |
вычислений, |
реализующих |
|||||||
исследования. Иначе |
говоря, |
компьютер позволяет произвести |
замену |
||||||||
физического, химического и т. д. эксперимента экспериментом вычислительным.
При |
проведении вычислительного эксперимента можно убедиться |
|
в необходимости и полезности последнего, особенно в |
случаях, когда |
|
провести |
натурный эксперимент затруднительно или |
невозможно. |
Вычислительный эксперимент, по сравнению с натурным, значительно дешевле и доступнее, его подготовка и проведение требует меньшего времени, его легко переделывать, он даёт более подробную информацию. Кроме того, в ходе вычислительного эксперимента выявляются границы
2
применимости математической модели, которые позволяют прогнозировать эксперимент в естественных условиях. Поэтому использование вычислительного эксперимента ограничивается теми математическими моделями, которые участвуют в проведении исследования. По этой причине вычислительный эксперимент не может заменить полностью эксперимент натурный, и выход из этого положения состоит в их разумном сочетании. В этом случае в проведении сложного эксперимента используется широкий спектр математических моделей: прямые задачи, обратные задачи, задачи оптимизации, задачи идентификации.
Использование вычислительного эксперимента как средства решения сложных прикладных проблем имеет в случае каждой конкретной задачи и каждого конкретного научного коллектива свои специфические особенности. Тем не менее, всегда чётко просматриваются общие характерные основные черты, позволяющие говорить о единой структуре этого процесса. В настоящее время технологический цикл вычислительного эксперимента принято подразделять на ряд технологических этапов. И хотя такое деление в значительной степени условно, оно позволяет лучше понять сущность этого метода проведения теоретических исследований.
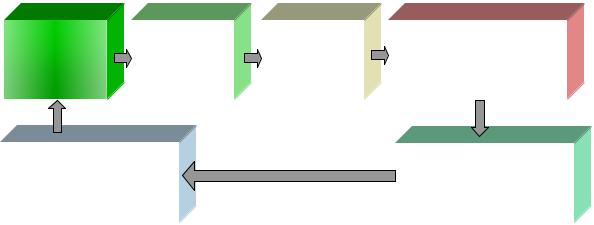
Таким образом, как и любой эксперимент, вычислительный эксперимент следует определенным правилам проведения. Схематически этапы вычислительного эксперимента можно представить следующим образом:
Объект |
Физическая |
|
Математическа |
|
Численный метод = |
|
|
дискретная модель + |
|||
|
модель |
|
модель |
|
|
исследования |
|
|
вычислительный |
||
|
|
|
|
||
|
|
|
|
алгоритм |
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведение вычислений |
|
Компьютерная |
и анализ результатов |
|
|
|
программа |
|
|
|
|
|
|
|
Рис. В. 1. Схема вычислительного эксперимента
Основу вычислительного эксперимента составляет триада: модель – метод (алгоритм) – программа. Сначала строится с некоторыми допущениями физическая модель объекта. Физическая модель—это ряд ограничений, предположений и упрощений, наложенных на рассматриваемое явление. Далее описывается математическая модель. Математическая модель—это уравнения, система уравнений или множество систем уравнений, которые с максимальной возможностью описывают физическую
3
модель. Затем необходимо решить эти системы уравнений. Как уже говорилось, обычно приходится применять численные методы. Под численным методом понимается совокупность дискретной модели, реализуемой на компьютере, и вычислительного алгоритма, позволяющего решить дискретизированную задачу. Для реализации численного метода необходимо разработать программу на одном из языков программирования или применить готовый пакет прикладных программ. В настоящее время существуют пакеты прикладных программ, такие как MathCAD, Matlab, Maple, Mathematica и другие, позволяющие решить большинство практически встречающихся задач. Однако грамотная постановка задачи, рациональный выбор метода решения и правильная интерпретация результатов требуют серьезных знаний численных методов. После отладки программы производятся вычисления на компьютере (обычно требуется провести много вариантов вычислений, для чего необходимо планировать вычислительный эксперимент) и анализ результатов. После получения результатов исследуется соответствие результатов вычислительного эксперимента процессу функционирования реального объекта и при необходимости уточняются компоненты схемы вычислительного эксперимента (рис. В.1) до получения удовлетворительных результатов.
3.Численные методы
Вшироком смысле под численным методом, как уже говорилось выше, понимается совокупность дискретной модели, реализуемой на компьютере, и вычислительного алгоритма, позволяющего решить дискретизированную задачу.
Одной и той же математической модели можно поставить в соответствие множество дискретных моделей и вычислительных алгоритмов, т. е. численных методов. При выборе численного метода необходимо учитывать две группы требований:
•дискретная модель должна быть адекватной математической модели;
•численный метод должен быть корректным и реализуемым на компьютере.
Для обеспечения адекватности дискретная модель должна обладать свойствами сходимости численного метода, выполнения дискретных аналогов сохранения и качественно правильного поведения решения.
Сходимость численного метода, например, означает, что при уменьшении шага разбиения интервала интегрирования точность численного интегрирования возрастает. Различные математические модели являются выражением физических законов сохранения, поэтому для дискретной модели законы сохранения также должны выполняться. Качественно правильное поведение дискретной модели означает, что из-за дискретного характера поведения модели не теряются некоторые детали поведения реальной системы.
4
Корректность численного метода означает, что дискретная задача должна быть однозначно разрешимой и устойчивой к погрешностям исходных данных и погрешностям вычислений. Реализуемость численного метода на компьютере ограничена объемом памяти и быстродействием компьютера. Вычислительный алгоритм должен предъявлять разумные требования к ресурсам компьютера. Например, математически корректный метод Крамера решения систем линейных алгебраических уравнений абсолютно неприменим для решения реальных задач: если принять, что каждая арифметическая операция выполняется за 10−6 с, то для решения системы с 20 неизвестными методом Крамера потребуется более миллиона лет. В то же время простейшим методом Гаусса эта система будет решена за доли секунды.
В узком смысле под численными методами понимают методы приближённого решения математических задач, сводящиеся к выполнению конечного числа элементарных операций над числами. В качестве элементарных операций фигурируют арифметические действия, выполняемые обычно приближённо, а также вспомогательные операции — записи промежуточных результатов, выборки из таблиц и т.п. Числа задаются ограниченным набором цифр в некоторой позиционной системе счисления (десятичной, двоичной и т.п.). Таким образом, в численных методах числовая прямая заменяется дискретной системой чисел (сеткой); функция непрерывного аргумента заменяется таблицей её значений в сетке; операции анализа, действующие над непрерывными функциями, заменяются алгебраическими операциями над значениями функций в сетке.
Целью курса "Численные методы" является изучение теоретических основ и получение практических навыков решения вычислительных задач и проведения вычислительного эксперимента.
5
