5. Отношения на множествах. Понятие подмножества.
Сравнение множеств:
Пусть во множестве A задано некоторое отношение "○".
1)Отношение "○" рефлексивно, если для любого элемента a из множества A выполнено a○a (т.е. любой элемент связан отношением ○ с самим собой). Например: отношение равенства на множестве отрезков рефлексивно, так как любой отрезок равен сам себе.
2)Отношение ○ симметрично, если из a○b следует b○a для любых элементов a и b множества A. Отношение равенства на множестве отрезков является симметричным, так как если [AB] = [CD], то и [CD] = [AB].
3)Отношение ○ называется транзитивным, если из того, что a○b и b○c следует, что a○c. В частности, отношение равенства отрезков транзитивно, так как если отрезок AB равен отрезку CD, а отрезок CD равен отрезку MN, то отрезок AB равен отрезку MN.
4)Отношение ○ во множестве A называется отношением эквивалентности, если оно одновременно рефлексивно, симметрично и транзитивно.
Множество В включает множество А, если каждый элемент А есть элемент В. В этом случае А называется подмножеством В, а В – надмножеством А. Если В включает А и А не равно В, то А называется собственным подмножеством В. Два множества равны, если они являются подмножествами друг друга.
Одно канторовское множество является подмножеством второго тогда и только тогда, когда любой элемент первого канторовского множества принадлежит второму.
6. n-арное отношение. Область определения.
N-арное отношение – подмножество произведения нескольких множеств.
Множество первых элементов упорядоченных пар, входящих в отношение R, составляет его область определения
Отношение — математическая структура, которая формально определяет свойства различных объектов и их взаимосвязи. Отношения обычно классифицируются по количеству связываемых объектов (арность) и собственным свойствам (симметричность, транзитивность и пр.). В математике примерами отношений являются равенство (=), коллинеарность, делимость и т. д.
n-местным (n-арным) отношением, заданным на множествах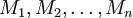 
, называется подмножество прямого произведения этих множеств.
7. Бинарное отношение.
Бинарным отношением из множества А в множество В называется подмножество прямого произведения А и В.
Бинарным отношением на множестве М называется подмножество R декартова квадрата М х М (т.е. подмножество множества всех упорядоченных пар элементов из М).