spoPresentation2

Лемма о разрастании КС - языка

Пусть L – КС-язык:

D L, р 1 > 0, |D|tp, G, E1,M,E2, J V* | D =

GE1ME2J, 0<|E1E2|dp, D’ = GE1iME2iJ, i 1t0, D’ L.

В любой достаточно длинной строке КСязыка всегда можно найти 2 подстроки с ненулевой суммарной длиной, одновременное повторение которых произвольное число раз порождает новые строки того же языка

181

Лемма о разрастании КС - языка

Пример

L = { 0n1n | nt1} КС

L = { 0n1n2n | nt1} не КС

182

Дерево вывода

Деревом вывода грамматики G(T,N,P,S) называется дерево (граф), которое соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:

каждая вершина обозначается символом грамматики V (T N {O}

корнем дерева является вершина, обозначенная аксиомой S

листьями являются вершины, обозначенные символом t (T {O})

183

Дерево вывода

если некоторый узел обозначен символом A N, а связанные с ним узлы символами

V1,V2,…,Vn, n>0, Vi (T N {O}), то в

грамматике G существует правило

Ao V1V2…Vn P

В таком виде дерево вывода всегда можно построить для КС и регулярных грамматик

Для других типов – только частные случаи

184

Дерево вывода

Пример

G ( {/,*,a,p,m}, {S,C,K} ,P, {S}),

P = { S o C*/ | Kpm

C o /* | C/ | C* | Ca | Cpm

будет иметь следующий вид:

185

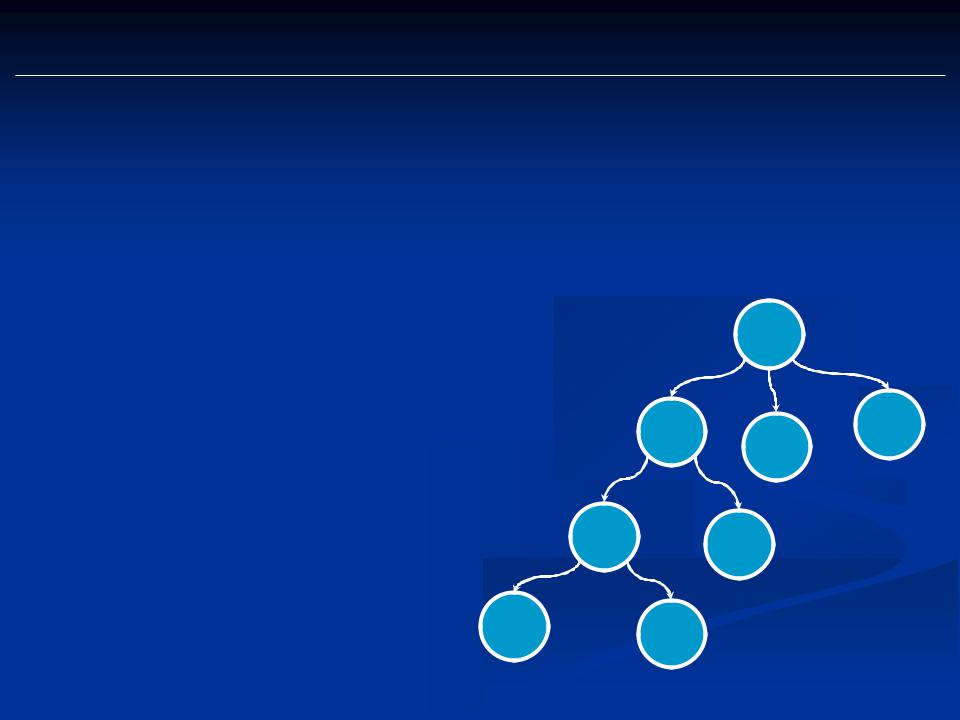
Дерево вывода

//apm

K a

/ /

186

Однозначность грамматики

Однако иногда одна и та же цепочка может иметь разные деревья вывода

Пример: G ( { (, a, b, ), *, + }, {S}, P, S)

P = { S o S+S | S*S | (S) | a | b }

цепочка a*b+a

Правосторонний вывод:

So S+So S*S+So a*S+So a*b+So a*b+a

Левосторонний вывод:

So S*So a*So a*S+So a*b+So a*b+a

188

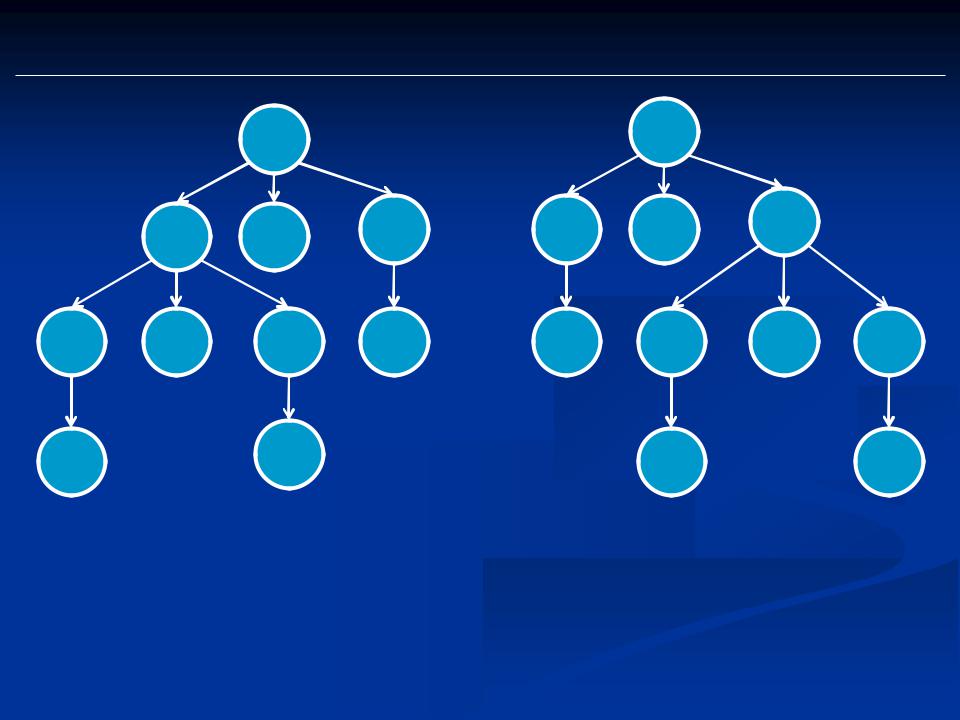
Однозначность грамматики

189

Однозначность грамматики

Однозначность – это свойство грамматики, а не языка

для языка, заданного неоднозначной грамматикой, может найтись однозначная грамматика, задающая тот же самый язык

Для построения компиляторов грамматики не должны допускать неоднозначности

Неоднозначность может устраняться заданием приоритетов

190