
- •1.Введение
- •2.Траектория и путь м.Т. Ск-ть м.Т.
- •3.Ускорение м.Т.
- •4.Поступат. И вращат. Движ. Тв. Тела.
- •6. Масса и Импульс тела
- •7.Центр масс
- •8.Закон сохранения импульса
- •9.Движение тела перем. Массы
- •10.Момент силы
- •11.Момент импульса
- •11.Закон сохранения момента импульса
- •13.Момент инерции
- •14.Энергия
- •15.Кинетическая энергия. Работа
- •16.Потенциальные (консервативные) силы. Потенциальная энергия
- •17.Закон сохр. Полной мех. Энергии
- •18.Кинетическая энергия вращательного движения
- •19.Плоское движение. Кинетическая энергия плоского движения
- •20.Неинерциальные системы отсчета
- •21.Колебание. Типы колебаний
- •22.Гармонические колебания
- •23.Метод вект. Диаграмм
- •24.Сложение двух гармонических колебаний
- •25.Упругая сила. Энергия гармонических колебаний
- •26.Потенциальная энергия. Полная энергия гармонич. Колебаний.
- •27.Пружинный маятник. Физический маятник
- •28.Математический маятник. Приведённая длина физического маятника
- •29.Затухающие механические колебания
- •30.Вынужденные механические колебания.
- •31.Упругие волны.Продольные и поперечные волны в упругой среде
- •32.Типы волн и их характеристики. Плоская синусоидальная волна
- •33.Сферическая и стоячие волны
- •34.Фазовая скорость упругих волн в твердой среде
- •35.Энергия упругой волны
- •36.Принцин относительности Галилея или преобразования Галилея
- •37.Специальная теория относительности. Преобразования Лоренца
- •38.Изменение длины тела
- •39.Промежуток времени между событиями
- •40.Основной закон релятивистской динамики
- •41.Релятивистский закон взаимодействия массы и энергии
- •42.Ур-ние Бернулли
- •43.Формула Торричелли. Ламинарный и турбулентный режимы движения вязкой среды
- •44.Статистический, динамический и термодинамический методы исследования.
- •45.Ф-я распределения вероятности
- •46.Распределение Максвелла.Средняя, среднеквадратичная и наивероятная скорости молекул.
- •47.Распределения Больцмана. Барометрическая формула
- •48.Ур-ние состояния идеальных газов
- •49.Число степеней свободы.Внутренняя энергия газа
- •50.Теплоемкость газов
14.Энергия
Энергией наз. скал. Физ. величина, явл-ся общей мерой различных форм движения материи, рассматриваемых в физике.
Эн. Сист. количественно хар-ет эту сист. в отношении возможных в ней превращений движения. Эти превращения происходят благодаря взаимодействию частей системы как друг с другом, так и с внешними телами, внешней средой.
Для анализа качественно различных форм движения и соответствующих сил взаимодействий в физике вводят различные типы энергии – механич., электромагнитн., ядерную и др.
Изменение мех. движения тела вызывается силами, действующими на него со стороны других тел.
Для количественного описания такого процесса обмена энергией между взаимодействующими телами в мех-ке пользуются понятием работы силы, приложенной к рассматриваемому телу.
Мех. эн. Бывает 2-х видов:
-кинетическая
-потенциальная.
Кинетическая эн. опред. массами и скоростями рассматриваемых тел.
Потенциальная эн. зависит от взаимного расположения взаимодействующих друг с другом тел.
15.Кинетическая энергия. Работа
Динамич.
ур-ние движения м.т. записывается формулой
 .
.
Умножим
скалярно обе части этого ур. на элементарное
перемещение частицы -
 :
: .
Мы можем записать
.
Мы можем записать ,
, ,
тогда левая часть ур-ния принимает вид
:
,
тогда левая часть ур-ния принимает вид
: .
В левую часть этого ур-ния внесем под
знак диф-ала (1)
.
В левую часть этого ур-ния внесем под
знак диф-ала (1) ,
где
,
где – результирующая внешних сил. Если
результир. внешн. сил = 0, то
– результирующая внешних сил. Если
результир. внешн. сил = 0, то т.е. величина
т.е. величина .
.
Если
внешняя сила
 ,
действующая на частицу, не равна 0, то
кинетич. эн. получит за время
,
действующая на частицу, не равна 0, то
кинетич. эн. получит за время приращение
приращение ,
где
,
где - перемещение частицы за время
- перемещение частицы за время Величина
Величина и = изменению кинетич. эн. наз. работой,
совершаемой силой
и = изменению кинетич. эн. наз. работой,
совершаемой силой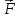 на перемещение тела на величину
на перемещение тела на величину и служит количественным описанием
процесса обмена энергией между
взаимодействующими телами, тогда
и служит количественным описанием
процесса обмена энергией между
взаимодействующими телами, тогда .
.
Предположим,
что за время
 точка перемещалась из положения 1 в
положение 2, тогда мы можем проинтегрировать
левую и правую части ур-ния
точка перемещалась из положения 1 в
положение 2, тогда мы можем проинтегрировать
левую и правую части ур-ния .
Левая часть этого ур-ния есть приращение
кинетич. Энергии частицы при перемещении
ее из т.1 в т.2. Правая часть есть работа
.
Левая часть этого ур-ния есть приращение
кинетич. Энергии частицы при перемещении
ее из т.1 в т.2. Правая часть есть работа силы
силы на пути от т.1 к т.2.
на пути от т.1 к т.2. или
или .
.
Из этого ур-ния следует, что результирующая всех сил, действующих на частицу, идет на приращение кинетич. эн. этой частицы.
Учитывая,
что работа есть величина скалярная,
формулу для работы можно переписать в
след. виде:
 ,
где
,
где – модуль силы;
– модуль силы; - путь, пройденный точкой под действием
силыF;
α – угол между векторами
- путь, пройденный точкой под действием
силыF;
α – угол между векторами
 . Если α – острый,
. Если α – острый, и
приращение энергии также положит., т.е.
кинетич. эн. увеличивается. Если α –
тупой,
и
приращение энергии также положит., т.е.
кинетич. эн. увеличивается. Если α –
тупой, и
приращение эн. также отрицат., энергия
убывает.
и
приращение эн. также отрицат., энергия
убывает.
В 1-м случае силу, кот. приложена к телу, наз. движущей силой, во 2-м – тормозящей.
Если
на мех. сист. одновременно действуют
силы

 …,
…, то
работа, совершаемая ими за малое время
то
работа, совершаемая ими за малое время = алгебраической сумме работ, совершаемых
за то же время
= алгебраической сумме работ, совершаемых
за то же время каждой их сил порознь.
каждой их сил порознь.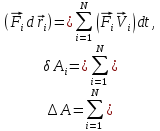 где
где – радиус-вектор точки приложения силы
– радиус-вектор точки приложения силы
 - ск-ть точки, к кот. приложена сила.
- ск-ть точки, к кот. приложена сила.
Работа
внутр. сил при любом перемещении абс.
тв. тела = 0. Поэтому при поступат. движ.
абс. тв. тела
 где
где - главный вект. внешних сил;
- главный вект. внешних сил; - радиус-вектор центра масс тв. тела.
- радиус-вектор центра масс тв. тела.
Работа,
совершаемая за единицу времени, наз.
мощностью и определяется формулой
 Тогда для мощности можно записать
формулу
Тогда для мощности можно записать
формулу , т.е. мощность = скалярн. произведению
силы на ск-ть м.т., к кот. приложена сила.
, т.е. мощность = скалярн. произведению
силы на ск-ть м.т., к кот. приложена сила.
