2.Траектория и путь м.Т. Ск-ть м.Т.

Линия, описываемая в пр-ве движущейся точкой, наз. траекторией этой точки.

Ур-ние траектории запис. в виде: z=z(x), y=y(x), т.е. чтобы найти ур-ние траектории, необходимо из ур-ния движ. м.т. исключить время. Длиной пути точки наз. сумма длин всех участков траектории, пройденных этой точкой за рассматриваемый промежуток времени.

Момент времени t=t₀ , раннее которого движение точки не рассматривалось, наз. начальным моментов времени, а положение т. в этот момент – начальным положением.

Длина пути S, пройденная точкой из ее нач. положения, явл. скалярной ф-ей времени и явл. положит. величиной S=S(t).

Вектором перемещения точки за промеж. вр. от t=t₁ до t=t₂ наз. вектор, проведенный из положения точки в момент времени t₁ в ее положение в момент времени t₂. Он равен разности радиус-векторов точки за рассматриваемый промежуток времени. 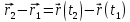. Вектор перемещения всегда направлен вдоль хорды, стягивающей соответствующий участок траектории.

Вектор приращения точки за промежуток времени от t до t+∆t равен 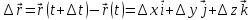, где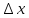,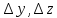– приращение координат на время ∆t.

М.т., свободно движущаяся в пр-ве, может совершать только 3 независимых движения, т.е. такие движения, каждое из кот. нельзя представить в виде комбинации остальных. Такие независимые движения наз. степенями свободы м.т.

Для хар-ки быстроты перемещения тел в пр-ве в мех-ке вводится понятие ск-ти. Средней ск-тью движущейся точки в интервале времени от t до t+∆t наз. вектор 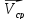= отношению приращения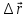радиус-вектора точки за время ∆t к продолжительности времени ∆t. .

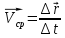Мгновенной ск-тью точки в момент времени t = пределу 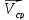при неограниченном уменьшении в продолжительности интервала ∆t: 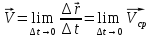=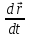, где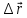– радиус вектор, кот. в проекциях на декартовую сист. коорд. записывается в след. виде.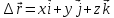

Путь dS, проходимый точкой за время dt, равен модулю вектора приращения dS=|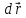|, тогда модуль вектора ск-ти равенv=||=.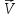

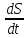Из этого следует, что разложение вектора 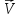по базису ПДСК имеет вид: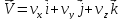. Проекции ск-ти точки на оси коорд. равны 1-м произв. по времени от соответствующих координат точки.,,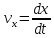

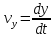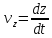
Модуль вектора ск-ти ||==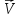

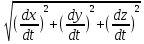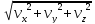
Движение точки наз. равномерным, если модуль ее ск-ти не изменяется с теч. времени. Если модуль вектора ск-ти возрастает с теч. вр., то движ. – ускоренное, если уменьшается – замедленное.

3.Ускорение м.Т.

Для хар-ки быстроты изменения ск-ти точки в мех-ке вводится понятие ускорение.

Средним ускорением точки в интервале времени от t до t+∆t наз. вектор 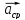= отношению приращения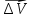точки за время ∆t. .

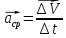Ускорением, или мгновенным ускорением наз. вект. величина 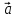, равная 1-й произв. по врем. от ск-ти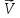рассм. точки или 2-й произв. по врем. от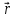этой точки..

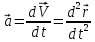Ускор. т. в мом. врем.t = пределу средн. ускор.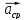при неограниченном уменьшении продолжительности интервала ∆t : .

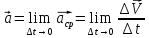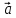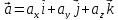Разложение вектора по базису ПДСК. Проекции ускор. на оси коорд. = 1-м произв. по врем.от соотв. проекций ск-ти, и 2-м произв. по врем. от соотв. коорд-т точки,,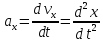

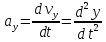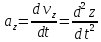
Модуль вектора ускорения

||==.

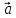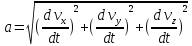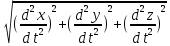Вектор ускор. м.т. лежит в соприкасающейся плоскости в проведенной т.М траектории и направлен в сторону вогнутости траектории ВС.

(Рис).

В этой плоскости вектор ускорения a можно разложить на 2 взаимно 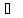составляющих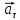и:+.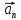

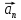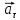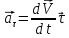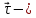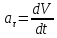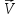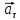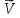Составляющая , направленная по касательной к траектории, наз.тангенциальным ускорен точки , гдеединичный вектор.,-проекция касательного ускорения на направление вектора. Векторыисовпадают по направлению при ускоренном движ. м.т. и противоположны – при замедленном. При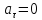движение наз. равномерный.

В общ. случае траектория точки представляет собой не плоскую, а пространственную кривую. Для такой кривой вводится понятие соприкасающейся плоскости. Соприкасающейся плоскостью в произвольной т.М кривой наз. предельное положение плоскости, проходящей через любые 3 точки кривой, когда эти точки неограниченно приближаются к т.М.

Составляющая 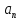ускоренияa м.т. наз. ее нормальным ускорением. Эта составляющая направлена по главной нормали траектории в т.М в сторону к центру кривизны траектории. Поэтому часто 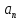наз. центростремительным ускорением.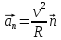, где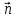- единичный вектор нормали,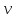– лин. ск-ть м.т.,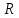– радиус кривизны траектории в т.М.