
- •1.Введение
- •2.Траектория и путь м.Т. Ск-ть м.Т.
- •3.Ускорение м.Т.
- •4.Поступат. И вращат. Движ. Тв. Тела.
- •6. Масса и Импульс тела
- •7.Центр масс
- •8.Закон сохранения импульса
- •9.Движение тела перем. Массы
- •10.Момент силы
- •11.Момент импульса
- •11.Закон сохранения момента импульса
- •13.Момент инерции
- •14.Энергия
- •15.Кинетическая энергия. Работа
- •16.Потенциальные (консервативные) силы. Потенциальная энергия
- •17.Закон сохр. Полной мех. Энергии
- •18.Кинетическая энергия вращательного движения
- •19.Плоское движение. Кинетическая энергия плоского движения
- •20.Неинерциальные системы отсчета
- •21.Колебание. Типы колебаний
- •22.Гармонические колебания
- •23.Метод вект. Диаграмм
- •24.Сложение двух гармонических колебаний
- •25.Упругая сила. Энергия гармонических колебаний
- •26.Потенциальная энергия. Полная энергия гармонич. Колебаний.
- •27.Пружинный маятник. Физический маятник
- •28.Математический маятник. Приведённая длина физического маятника
- •29.Затухающие механические колебания
- •30.Вынужденные механические колебания.
- •31.Упругие волны.Продольные и поперечные волны в упругой среде
- •32.Типы волн и их характеристики. Плоская синусоидальная волна
- •33.Сферическая и стоячие волны
- •34.Фазовая скорость упругих волн в твердой среде
- •35.Энергия упругой волны
- •36.Принцин относительности Галилея или преобразования Галилея
- •37.Специальная теория относительности. Преобразования Лоренца
- •38.Изменение длины тела
- •39.Промежуток времени между событиями
- •40.Основной закон релятивистской динамики
- •41.Релятивистский закон взаимодействия массы и энергии
- •42.Ур-ние Бернулли
- •43.Формула Торричелли. Ламинарный и турбулентный режимы движения вязкой среды
- •44.Статистический, динамический и термодинамический методы исследования.
- •45.Ф-я распределения вероятности
- •46.Распределение Максвелла.Средняя, среднеквадратичная и наивероятная скорости молекул.
- •47.Распределения Больцмана. Барометрическая формула
- •48.Ур-ние состояния идеальных газов
- •49.Число степеней свободы.Внутренняя энергия газа
- •50.Теплоемкость газов
45.Ф-я распределения вероятности
Пусть имеется сов-ть очень большого числа N одинаковых молекул, находящихся в равновесном состоянии (сост. сист. наз. равновесным, если ее состояние не изменяется с течением времени, причем равновесность состояния не связана с процессами, происходящими во внешней среде).
Предположим,
что некоторая величина
 ,
хар-ющая некоторое число молекул, может
принимать ряд дискретных значений
,
хар-ющая некоторое число молекул, может
принимать ряд дискретных значений . это значит, что из всего ансамбля
молекул всегда найдутся
. это значит, что из всего ансамбля
молекул всегда найдутся молекул, которые имеют значения величины
молекул, которые имеют значения величины .
Величина
.
Величина (1) наз. вероятностью того, что величина
(1) наз. вероятностью того, что величина имеет значение
имеет значение , причем
, причем ,
тогда
,
тогда , т.е. сумма вероятностей всех возможных
значений величины
, т.е. сумма вероятностей всех возможных
значений величины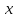 = 1.
= 1.
Допустим,
что молекулы характеризуются значениями
2-х физ. величин
 ,
каждая из которых может принимать ряд
дискретных значений
,
каждая из которых может принимать ряд
дискретных значений
 .
Согласно формуле (1), вероятности этих
значений равны
.
Согласно формуле (1), вероятности этих
значений равны
 ,
если значение одной из величин не зависит
от значения другой, то величины
,
если значение одной из величин не зависит
от значения другой, то величины наз. статистически независимыми.
наз. статистически независимыми.
Вероятность
того, что статистически независимые
величины имеют одновременно значения
 и
и , выражается формулой
, выражается формулой , т.е. вероятности умножаются.
, т.е. вероятности умножаются.
Теорема об умножении вероятностей говорит, что вероятность одновременного появления статически независимых событий = произведению вероятностей этих событий.
Сейчас
рассм. случай, когда величина
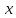 имеет значения, заключенные в пределах
малого интервала
имеет значения, заключенные в пределах
малого интервала .
.
![]()
и
определим, какова вероятность этого
события. Очевидно, что при малом
 это вероятность пропорциональна этому
это вероятность пропорциональна этому ,
и если значение величины
,
и если значение величины вдоль осиX
задается какой-то ф-ей f(x),
то вероятность того, что величина
вдоль осиX
задается какой-то ф-ей f(x),
то вероятность того, что величина
 будет нах-ся в интервале
будет нах-ся в интервале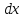 определится формулой
определится формулой а ф-яf(x)
задает место расположения этого интервала
а ф-яf(x)
задает место расположения этого интервала
 .
Ф-яf(x)
наз. ф-ей распределения вероятности,
или плотностью вероятности.
.
Ф-яf(x)
наз. ф-ей распределения вероятности,
или плотностью вероятности.
Умножив
 на полное число молекулN,
мы получим количество
на полное число молекулN,
мы получим количество
 молекул
молекул ,
обладающих значениямиx
и заключенных в пределах интервала
,
обладающих значениямиx
и заключенных в пределах интервала
 .
.

Тогда
интеграл, взятый по всему интервалу
возможных значений x,
т.е. сумма
 ,
должен равняться полному числу молекулx.
,
должен равняться полному числу молекулx.

Поскольку
число молекул N
постоянно, мы получим

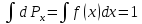
Среднее
значение величины x
в теории вероятности дается формулой
 (2).
(2).
Если
величина x
задается ф-ей
 ,
то ур-ние (2) принимает вид:
,
то ур-ние (2) принимает вид:
Напр.,
 ,
то
,
то
46.Распределение Максвелла.Средняя, среднеквадратичная и наивероятная скорости молекул.
Предполагаем,
что состояние газа равновесное, рассм.
распределение молекул газа по скоростям.
Введем воображаемое пр-во скоростей в
котором каждой отдельной молекуле в
ПДСК будут соответствовать ск-ти
 ,
, ,
, , т.е. в этом пространстве каждой молекуле
будет соответствовать точка, наз-емаямолекулярной
точкой(М.точкой).
, т.е. в этом пространстве каждой молекуле
будет соответствовать точка, наз-емаямолекулярной
точкой(М.точкой).
В
равновесном состоянии молекулы газа
движутся хаотично и все направленные
движения молекул равноправны и положение
м.точек относительно начала координат
сферически симметрично. В этом случае
плотность М.точек, т.е. число их в единице
объема V
пр-ва явл-ся ф-ей расстояния от начала
координат, т.е. ф-ей модуля ск-ти.
Во сколько раз увеличивается число молекул газа в объеме, во столько же раз возрастает плотность М.точек, а плотность М.точек пропорциональна числу молекул N. Nогда плотность М.точек можно представить в виде функции Nf(v).
Зная
вид ф-ции f(v)
можно найти число молекул
 , компоненты скорости которых заключены
в пределах интервалов
, компоненты скорости которых заключены
в пределах интервалов ,
, ,
, , лежащих в окрестности геом. точки с
координатами
, лежащих в окрестности геом. точки с
координатами ,
, ,
,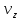 .
.
Если
взять объем прямоуг. параллелепипеда
со сторонами
 ,
, ,
, , то в этом объеме будет нах-ся
, то в этом объеме будет нах-ся ,
, ,
, N
точек.
N
точек.
Если
в соответствии с нашим рисунком
рассматривать шаровой слой радиусом V
и толщиной dv,
то молекулы, находящиеся в этом слое,
обладают скоростями, модули которых
лежат в интервале от V
до V+dv.
Чтобы найти число
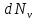 таких молекул, нужно умножить плотность
М.точек, соответствующих данному
значению, на объем шарового слоя, равный
таких молекул, нужно умножить плотность
М.точек, соответствующих данному
значению, на объем шарового слоя, равный , т.е.
, т.е.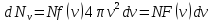 ,
гдеf(v)
– функция распределения вероятности
значений скорости V.
Эту ф-ю теоретически получил Максвелл
и она имеет вид
,
гдеf(v)
– функция распределения вероятности
значений скорости V.
Эту ф-ю теоретически получил Максвелл
и она имеет вид

Где
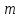 - масса молекулы
- масса молекулы
 -
постоянная Больцмана
-
постоянная Больцмана
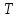 -
абсолютная температура
-
абсолютная температура
Коэф.
пропорциональности А определяется из
условия
 , кот. наз. условием нормировки ф-и
, кот. наз. условием нормировки ф-и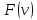 .
.
Соответствующий
расчет для коэффициента А дает ее
значение
 .
.
Тогда окончательное выр. для ф-и распределения молекул газа по скоростям запис. в виде:

Эта
ф-я наз. ф-ей распределения Максвелла.
В этой формуле под знаком
 стоит выр.
стоит выр. т.е. отношение кинетич. эн. молекулы для
данной скорости
т.е. отношение кинетич. эн. молекулы для
данной скорости к величине КТ, хар-ющей среднее значение
тепловой энергии молекул.
к величине КТ, хар-ющей среднее значение
тепловой энергии молекул.
Наиболее
вероятной скоростью, которой обладает
молекула газа
 ,
будет скорость, отвечающаяmax-муму
ф-и
,
будет скорость, отвечающаяmax-муму
ф-и
 .
Ее значения можно найти приравняв к
нулю производную
.
Ее значения можно найти приравняв к
нулю производную .
Исключив из нее коэф-ты, не зависящие
от скоростиv
:
.
Исключив из нее коэф-ты, не зависящие
от скоростиv
:
 .
.
Продиф-вав
это ур-ние
 .
.
Значение,
кот. соответствует max-муму
наиверостной ск-ти, опред-ся из равенства
 ;
;
Из
формул для ф-и распределения вероятности
для средней арифметической ск-ти мы
можем записать
 , где
, где - значение ск-ти при данной температуреT.
- значение ск-ти при данной температуреT.
Тогда
средняя квадратичная ск-ть
 и значение ее
и значение ее .
.
