32.Типы волн и их характеристики. Плоская синусоидальная волна

Волна называется плоской, если ее волновые поверхности представляют сов-ть плоскостей, || друг другу.

В плоской волне, распространяющейся вдоль оси Ох, все величины S, хар-щие колебат. движ. среды, зависят только от времени t и координаты x, рассматриваемой т.М среды.

Если в среде нет затухания, то колебания в т.М отличаются от колеб. в нач. коорд. x=0 только тем, что они сдвинуты по времени на величину , где- ск-ть волны, поэтому в плоской волне, распространяющейся вдоль положит. направления оси Ох,S явл. ф-ей разности и ур-ние такой плоской волны имеет вид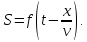

Ур-ние плоской синусоид. волны, распространяющейся в непоглощающей среде, вдоль положит. направления Ох, имеет вид: илигдеA – амплитуда колеб., амплитуда волны; 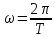- циклич. или круговая частота волны;- период колеб.;- нач. фаза колеб. в мом. времениt=0 в точке коорд. плоскости x=0.

Величина , равная фазе колеб. в произвольной точке с коорд.x, наз. фазой плоской сферич. волны.

Расстояние , на кот. распространяется синусоид. волна за время, = периоду колеб., наз. длиной волны.

Длина волны = расстоянию между двумя ближайшими точками среды, в кот. разность фаз. колеб. = . Тогда ур-ние плоской синусоид. волны можно представить в виде:

, где наз. волновым числом и фаза плоской синусоид. волны.

33.Сферическая и стоячие волны

Волна наз. сферич., если ее волновые пов-ти имеют вид концентрических сфер. Центр этих сфер наз. центром волны.

Ур-ние расходящ. сферич. волны имеет вид , где– расстояние от центра волны до рассматриваемой т.М среды;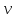- ск-ть волны.

Ур-ние синусоид. сферич. волны : , где– амплитуда волны;- физ. величина, численно равная амплитуде волны на единичном расстоянии от ее центра;- нач. фаза колебаний в центре волны.

Распространение плоской и расходящейся сферических волн в однородной изотропной среде описывается ДУ частных производных, кот. наз. волновым ур-нием или, гдеи наз. оператором Лапласа скалярного поля.;– физ. величина, кот. хар-ет возмущение, распространяющееся в среде со скоростью.

Скорость распространения синусоид. волны наз. фазовой ск-тью. Она равна ск-ти перемещения в пр-ве точек пов-ти, соответствующей любомуfix значению фазы синусоид. волны.

Для плоской синусоид. волны мы имеем выражение для фазы .

Продиф-ем это выр. один раз по t и по x.

т.к. ., т.е. фазовая ск-ть связана с циклич. частотой и волновым числом.

Для сферич. синусоид. волны может записать для ск-ти .

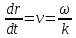Стоячей волной наз. волна, образующаяся в рез-те наложения 2-х бегущих синусоид. волн, распространяющихся навстречу друг другу и имеющих одинаковые частоты и амплитуды.

Ур-ние стоячей волны имеет вид:

Из этого ур-ния видно, что амплитуда стоячей волны = : . Точки, где, наз. узлами, а где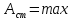– пучностями стоячей волны.

34.Фазовая скорость упругих волн в твердой среде

Рассм. цилиндрич. стержень из однородного и изотропного материала

Предположим, что вдоль стержня распространяется плоская гармонич. волна. Частицы, лежащие в сечении стержня определяем координатой х, будут претерпевать смешение S, описываемое ур-нием (1).

Выделим в стержне элемент длины ∆x, ограниченной в отсутствие волны значением координаты x и x+∆x.

Если сечение стержня в некоторый момент времени имеет смещение S, т.е. в момент возникновения волны, то смещение с координатой x+∆x будет S+∆S. Т.к. смещение сечений для разных значений координаты x описывается формулой (1), то они не одинаковы для разных x и этот элемент стержня будет деформирован. Он получает удлинение ∆S ≠∆x.

Отношение – среднее значение относительного удлинения элемента стержня ∆x.

Чтобы получить деформацию S в сечении с координатой x нужно устремить

Относит. удлинение =, где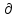- частная производнаяS по x, т.к. в общем случае S зависит от x и t.

Деформация растяжения приводит к появлению в сечении с координатой x нормального упругого напряжения, описываемого формулой. 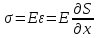,E – модуль Юнга.

Появление деформации в стержне приводит к появлению силы, проекция кот. на ось X равна 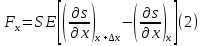, где - площадь поперечного сечения стержня. Т.к. 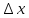мало, то мы можем воспользоваться св-вом производных для бесконечно малых величин: .

Если подставить это выр. в ур-ние (2), то выр. для проекции силы перепишется в виде Для этого случая мы можем записать динамич. ур-ние движения 2-го зак. Ньютона.

Учитывая, что масса = 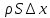и подставив это значение, мы можем записать равенство . Сделав сокращение, получим волновое ур-ние . (3).

Ур-ние для плоской синусоид волны, распространяющейся вдоль оси X : 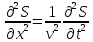(4).

Сравнив ур-ния (3) и (4) получим выражение для фазовой ск-ти продольных упругих волн стержня : .

Для поперечных волн: 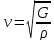, гдеG – модуль сдвига.