2.2.1. Прямые методы решения слау

1. Правило Крамера

Рассмотрим систему (1). Как отмечалось выше, если определитель этой системы не равен нулю, то будет иметь место единственное решение. Это необходимое и достаточное условие. Тогда по правилу Крамера

, (4)

где D_k– определитель, получающийся изDпри замене элементовa_1k,a_2k, ...,a_nkk-го столбца (соответствующими) свободными членамиb₁,b₂, ...,b_nиз (1), или

,

где А_ikалгебраическое дополнение элементаa_ikв определителеD. Стоит существенная проблема вычисления определителей высоких порядков.

2. Метод обратных матриц

Дана система . Умножим левую и правую части этого выражения наА^–1:

;.

При его реализации стоит проблема нахождения обратной матрицы А^–1, с выбором экономичной схемы ее получения и с достижением приемлемой точности. Эти вопросы рассмотрим ниже.

3. Метод Гаусса

Этот метод является наиболее распространенным методом решения СЛАУ. В его основе лежит идея последовательного исключения неизвестных, в основном, приводящая исходную систему к треугольному виду, в котором все коэффициенты ниже главной диагонали равны нулю. Существуют различные вычислительные схемы, реализующие этот метод. Наибольшее распространение имеют схемы с выбором главного элемента либо по строке, либо по столбцу, либо по всей матрице. С точки зрения простоты реализации, хотя и с потерей точности, перед этими схемами целесообразней применять так называемую схему единственного деления. Рассмотрим ее суть.

Посредством первого уравнения системы (1) исключается х₁из последующих уравнений. Далее посредством второго уравнения исключаетсях₂из последующих уравнений и т.д. Этот процесс называетсяпрямым ходом Гаусса. Исключение неизвестных повторяется до тех пор, пока в левой части последнегоn-го уравнения не останется одно неизвестноех_n

a_nnx_n = b, (5)

где a_nn иb– коэффициенты, полученные в результате линейных (эквивалентных) преобразований.

Прямой ход реализуется по формулам

а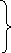*_mi = a_mi – ;

b*_m = b_m – (6)

где m– номер уравнения, из которого исключаетсяx_k;

k– номер неизвестного, которое исключается из оставшихся (n –k) уравнений, а также обозначает номер уравнения, с помощью которого исключаетсяx_k;

i– номер столбца исходной матрицы;

a_kk– главный (ведущий) элемент матрицы.

Во время счета необходимо следить, чтобы a_kk0. В противном случае прибегают к перестановке строк матрицы.

Обратный ход метода Гауссасостоит в последовательном вычисленииx_n,x_n–1, ...,x₁, начиная с (5) по алгоритму

x_n = b / a_nn ; . (7)

Точность полученного решения оценивается посредством «невязки» (3). В векторе невязки (r₁,r₂, ... ,r_n)^Тотыскивается максимальный элемент и сравнивается с заданной точностью. Приемлемое решение будет, еслиr_max<. В противном случае следует применить схему уточнения решения.

Уточнение корней

Полученные методом Гаусса приближенные значения корней можно уточнить.

Пусть для системы найдено приближенное решение, не удовлетворяющее по «невязке». Положим тогда. Для получения поправки= (₁,₂, ...,_n)^Ткорняследует рассмотреть новую систему

или,

где – невязка для исходной системы.

Таким образом, решая линейную систему с прежней матрицей Аи новым свободным членом= (₁,₂, ...,_n)^Т, получим поправки (₁,₂, ...,_n).

Пример решения СЛАУ по методу Гаусса (с точностью до трех знаков). Нужно уточнить корни до 10^–4:

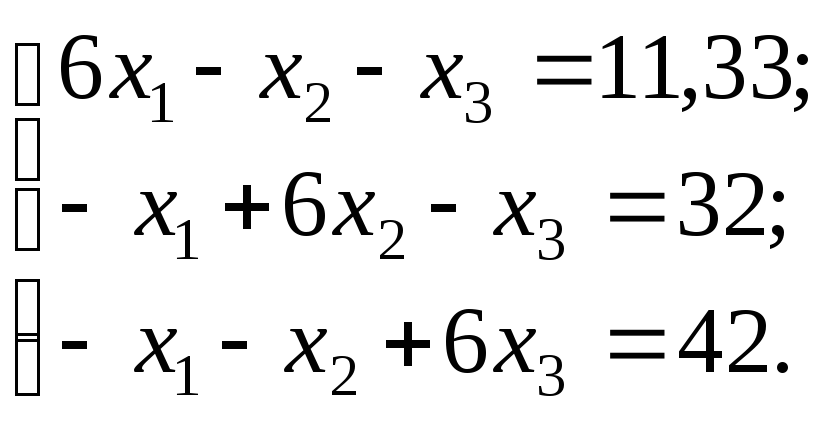
В результате = 4,67;= 7,62;= 9,05. Невязки равны= −0,02;= 0;= −0,01. Получено уточнение= −0,0039;= −0,0011;= −0,0025. Следовательнох₁ = 4,6661;х₂ = 7,6189;х₃ = 9,0475. Невязки будут₁ = −210^–4;₂ = −210^–4;₃ = 0.