
- •В. П. Кузнецов, с. В. Лукьянец, м. А. Крупская теория автоматического управления
- •Часть 2 Дискретные системы, нелинейные системы, случайные процессы в системах автоматического управления
- •Isbn 978-985-488-070-9 (ч.2)
- •Isbn 978-985-488-048-8
- •Содержание
- •Предисловие
- •1. Дискретные системы автоматического управления
- •1.1.Основные понятия и классификация
- •1.2. Решетчатые функции, разностные уравнения и дискретное преобразование Лапласа
- •1.3. Описание разомкнутых импульсных систем
- •1.4. Частотные характеристики импульсных систем
- •1.5 Характеристики замкнутых импульсных систем
- •1.6. Процессы в импульсных системах
- •1.7. Устойчивость процессов в импульсных системах
- •1.8. Точность импульсных систем
- •1.9. Оценки качества импульсных систем
- •1.10.Условия эквивалентности импульсных и непрерывных сау
- •1.11. Элементы синтеза импульсных систем
- •1.12.Уравнения состояния линейных импульсных систем
- •1.13. Характеристики импульсных систем, описываемых уравнениями в пространстве состояний
- •1.14. Цифровые системы автоматического управления
- •1.15. Исследование цифровых систем автоматического управления
1.12.Уравнения состояния линейных импульсных систем
Так же как и непрерывные системы [1], импульсные можно описывать с помощью векторно-матричных уравнений, называемых уравнениями состояния.
Уравнениями состояния линейной импульсной системы называются уравнения вида
 (1.80)
(1.80)
где
![]() − вектор
состояния
системы,
− вектор
состояния
системы,
![]() − вектор
входа
системы,
− вектор
входа
системы,
![]() − вектор
выхода системы,
− вектор
выхода системы,
![]() − основная
матрица
системы размерности
− основная
матрица
системы размерности
![]() ,
,![]() − матрица
входа системы
размерности
− матрица
входа системы
размерности
![]() ,
, ![]() − матрица выхода системы размерности
− матрица выхода системы размерности ![]() ,
,![]() − дискретное
время.
− дискретное
время.
Первое
уравнение в (1.80)− уравнение
входа
системы, второе − уравнение
выхода.
Уравнениями (1.80) описываются как
многомерные системы, когда
![]() ,
,![]() − вектора,
так и одномерные системы, когда
− вектора,
так и одномерные системы, когда![]() ,
,![]() − скалярные
величины.
− скалярные
величины.
Рассмотрим
методику получения уравнений (1.80) для
разомкнутой импульсной системы,
изображенной на рис. 1.4. Вход
![]() и выход
и выход![]() линейного непрерывного звена с
передаточной функцией
линейного непрерывного звена с
передаточной функцией![]() можно описать с помощью уравнений
состояния [1]:
можно описать с помощью уравнений
состояния [1]:
 (1.81)
(1.81)
где
коэффициенты матриц
![]() размерности
размерности![]() ,
,![]() размерности
размерности![]() и
и![]() размерности
размерности![]() находятся по передаточной функции
находятся по передаточной функции![]() .
.
Используя
матрицу
![]() ,
можно найти [1] переходную матрицу
состояния непрерывной системы (1.81),
которую обозначим
,
можно найти [1] переходную матрицу
состояния непрерывной системы (1.81),
которую обозначим![]() ,
и записать общее уравнение первого
(дифференциального) уравнения (1.81) в
виде
,
и записать общее уравнение первого
(дифференциального) уравнения (1.81) в
виде

где
![]() − момент
приложения внешнего воздействия
− момент
приложения внешнего воздействия![]() ,
,![]() − начальное
значение вектора состояния при
− начальное
значение вектора состояния при![]() .
Сигнал
.
Сигнал![]() с выхода ФУ представляет собой
последовательность прямоугольных
импульсов длительности
с выхода ФУ представляет собой
последовательность прямоугольных
импульсов длительности![]() и высоты
и высоты![]() ,
поступающих в моменты времени
,
поступающих в моменты времени![]() .
Рассмотрим произвольный
.
Рассмотрим произвольный![]() -ый
момент времени
-ый
момент времени![]() и обозначим значение вектора состояния
при
и обозначим значение вектора состояния
при![]() через
через![]() .
Тогда реакция системы (выход звена) на
.
Тогда реакция системы (выход звена) на![]() -ый
импульс будет
-ый
импульс будет
 (1.82)
(1.82)
Обозначим
при
![]() (момент окончания импульса) значение
вектора
(момент окончания импульса) значение
вектора![]() через
через![]() .
Тогда во время паузы в
.
Тогда во время паузы в![]() -ом
периоде сигнал на выходе звена будет
определяться выражениями:
-ом
периоде сигнал на выходе звена будет
определяться выражениями:
 (1.83)
(1.83)
Из
(1.82) находим при
![]() вектор
вектор![]() ,
подставляем его в (1.83) и окончательно
получаем
,
подставляем его в (1.83) и окончательно
получаем
 (1.84)
(1.84)
Положим
в (1.84)
![]() и, используя свойства переходной матрицы
состояния
и, используя свойства переходной матрицы
состояния![]() ,
получим
,
получим
 .
.
Сделав
под интегралом замену переменной
![]() и с учетом
и с учетом![]() ,
получим
,
получим

Обозначим числовые матрицы
![]() ,
, ,
,![]() , (1.85)
, (1.85)
а
векторы
![]() ,
,![]() ,
,![]() ,
,![]() через
через![]() ,
,![]() ,
,![]() ,
,![]() .
Окончательно получим уравнения состояния
разомкнутой импульсной системы вида
(1.80)
.
Окончательно получим уравнения состояния
разомкнутой импульсной системы вида
(1.80)
 (1.86)
(1.86)
Приведенная методика получения разностных уравнений разомкнутой импульсной системы обобщает подход, изложенный в подразделе 1.2 при выводе уравнения (1.15).
Напомним
[1] один из возможных способов определения
вида матриц
![]() ,
,![]() ,
,![]() в (1.81) с использованием передаточной
функции
в (1.81) с использованием передаточной
функции![]() линейной непрерывной части системы.
Пусть
линейной непрерывной части системы.
Пусть![]() − дробно-рациональная
функция переменной
− дробно-рациональная
функция переменной![]() и уравнение
и уравнение![]() имеет
имеет![]() различных корней
различных корней![]() ,
тогда
,
тогда
 ,
, ,
,![]() , (1.87)
, (1.87)
где
 ,
, .
.
Если
![]() − диагональная
матрица (87), то нетрудно найти
− диагональная
матрица (87), то нетрудно найти![]() ,
,![]() ,
,![]() ,
,![]() в (1.86)
в (1.86)
 ,
, ,
,
 ,
,![]() .(1.88)
.(1.88)
В
случае кратных корней
![]() матрица
матрица![]() будет в форме Жордана.
будет в форме Жордана.
Получим
уравнения состояния замкнутой линейной
импульсной системы рис. 1.3. С учетом
уравнения замыкания
![]() из (1.86) получим уравнения состояния
замкнутой импульсной системы
из (1.86) получим уравнения состояния
замкнутой импульсной системы
 (1.89)
(1.89)
где
![]() − основная
матрица замкнутой системы.
− основная
матрица замкнутой системы.
Возможно
также получение уравнений состояния
импульсной системы с использованием
в качестве исходных передаточной
функций разомкнутой ![]() или замкнутой
или замкнутой ![]() импульсной системы,
либо соответствующих разностных
уравнений [5].
импульсной системы,
либо соответствующих разностных
уравнений [5].
Пример 1.12.
Пусть в разомкнутой импульсной системе
 .
Уравнение
.
Уравнение![]() имеет два корня
имеет два корня![]() ,
, .
Находим
.
Находим![]() ,
,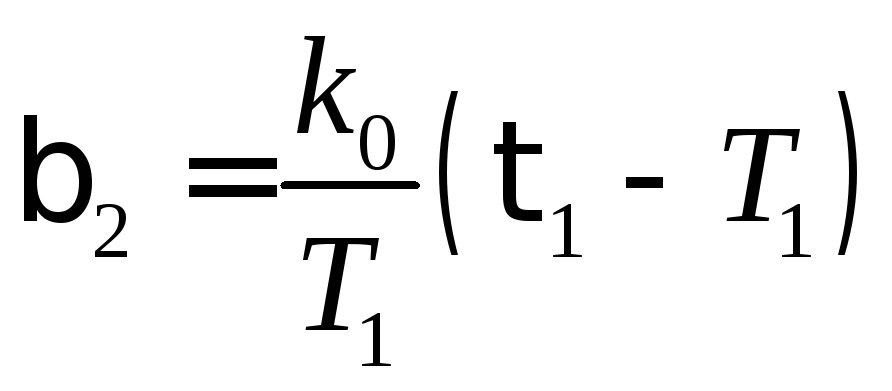 .
В соответствии с (1.88) определяем матрицы
.
В соответствии с (1.88) определяем матрицы![]() ,
,![]() ,
,![]() .
Окончательно уравнения состояния
разомкнутой импульсной системы будут
.
Окончательно уравнения состояния
разомкнутой импульсной системы будут
 (1.90)
(1.90)
