2.3.3. Построение фазовых траекторий

Аналитическое выражение для фазовой траектории является решением нелинейных дифференциальных уравнений (2.13), (2.14) и найти его в общем случае невозможно. Однако если представить реальные нелинейные характеристики в виде идеальных, т.е. аппроксимированных на отдельных участках прямыми линиями, то возможно применение аналитических методов решения. Суть такого подхода заключается в следующем. Пусть идеальная нелинейность на некотором интервале описывается линейной характеристикой , где– заданные коэффициенты. В этом случае уравнение (2.13) для фазовых траекторий будет иметь вид

, (2.18)

где ,,,,,.

Уравнение (2.18) является частным случаем уравнения Якоби и может быть проинтегрировано, т.е. задавая начальные значения ,можно найти вид фазовой траекториипри условии, что.

Таким образом, разбивая всю ось на ряд интервалови аппроксимируя нелинейностьлинейной зависимостьюна каждом интервале, получим свое уравнение (2.18), решение которого даст на этом интервале некоторою фазовую траекторию. Линии, соответствующие равенствамна плоскости, разделят ее на ряд областей. Эти линии, границы областей, будем называтьлиниями переключения.

При попадании изображающей точки фазовой траектории на линию переключения, конечное значение этой фазовой траектории, т.е. значения координат ина ее конце, принимаются за начальные условия для фазовой траектории в смежной области. Такой метод решения дифференциального уравнения называют методомсшивания, склеивания или припасовывания решений.

Другой способ построения фазовых траекторий – это метод изоклин, который является графическим методом. В уравнении для фазовых траекторий (2.13) правая часть в каждой точке фазовой плоскости с координатами ,определяет скорость движения изображающей точки, т.е. определяет угол наклона касательной к фазовой траектории в этой точке. Уравнение

, (2.19)

где произвольное число, определяет линию на фазовой плоскости равных значений производных или углов наклона касательной. Эту линию и называютизоклиной.

Изобразив на фазовой плоскости несколько изоклин с соответствующими направлениями касательных, можно приближенно представить вид фазовых траекторий и вид фазового портрета.

Наконец, возможно построение фазового портрета путем моделирования уравнений фазовых траекторий и их решения на компьютере.

2.3.4. Скользящие режимы в нелинейных системах

Рассмотрим нелинейную САУ [7], изображенную на рис. 2.7, где – модель идеального реле:при,при.

Рис. 2.7

В соответствии с рис. 2.7 уравнение системы будет

.

Вводя новые переменные ,, получим систему уравнений

из которой находим уравнения для фазовых траекторий

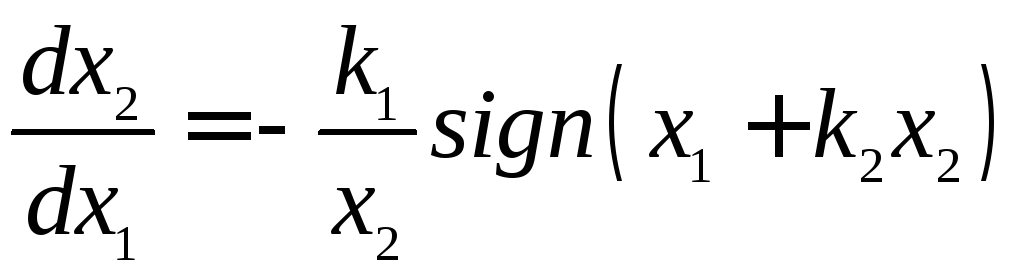. (2.20)

Уравнение линии переключения получим из условия , т.е.

. (2.21)

В области фазовой плоскости при уравнение (2.20) имеет вид

, (2.22)

а там где , уравнение (2.20) будет

. (2.23)

Решения уравнений (2.22), (2.23) соответственно имеют вид:

, (2.24)

, (2.25)

где ,произвольные постоянные, которые определяются начальными условиями,.

Уравнения (2.24), (2.25) на фазовой плоскости определяют параболы. Уравнение (2.24) справедливо справа от линии переключения (2.21), а (2.25) – слева.

На рис. 2.8 изображен фазовый портрет нелинейной системы, из которого следует, что на линии переключения существует отрезок АВ, на котором все фазовые траектории с двух сторон входят в этот отрезок. Изображающая точка, попав на этот отрезок, далее с течением времени обязана двигаться по нему к началу координат (положению равновесия). Такой режим называется скользящим режимом, а отрезок АВ отрезком скольжения. На рис. 2.8 начальная точка переходит по фазовым траекториям в точку, затем в(попадает на отрезок скольжения) и далее по линии переключения обязана двигаться к началу координат, т.е. в системе возникает режим скольжения.

Рис. 2.8

Найдем координаты точек А, В, т.е. длину отрезка скольжения. В точке А касательная к параболе должна совпадать с линией переключения, т.е. . Тогда с учетом (2.22) будем иметь, т.е. ордината точкиА будет .

Аналогично, ордината точки В будет . Таким образом, длина отрезкаАВ будет тем больше, чем больше или.

Найдем закон движения в скользящем режиме. На линии переключения (2.21) , но, откуда имеет место следующее уравнение

, (2.26)

определяющее закон движения в скользящем режиме. Решение уравнения (2.26) имеет вид .

Таким образом, на линии скольжения исходная нелинейная система второго порядка вырождается в линейную систему первого порядка (2.26), причем параметры процесса скольжения не зависят от параметров прямой цепи . Меняя, можно менять время попадания изображающей точки в начало координат, т.е. фактически время регулирования. Чем меньше величина, тем меньше время регулирования.