1.4. Повторение независимых опытов

Пусть производится n независимых опытов. В результате каждого опыта событие A появляется с вероятностью р и не появляется с вероятностью 1-р . Вероятность P(n,k) того, что в последовательности из n опытов интересующее нас событие А произойдет ровно k раз (формула Бернулли) равна

(1.21)

Пусть производится серия из n независимых испытаний, в результате каждого из которых может появиться одно из событий A₁, A₂, ..., A_r с вероятностями p₁, p₂, ..., p_r соответственно.

Вероятность того, что в серии из n испытаний событие A₁ наступит ровно k₁ раз, событие A₂ — k₂ раз, ... , событие A_r — k_r раз (k₁ + ... + k_r = n) равна

(1.22)

Локальная теорема Лапласа

Вероятность того, что в n независимых испытаниях (n-достаточно большое число), в каждом из которых вероятность появления события равна p, событие наступит ровно k раз, приближенно равна

(1.23)

где

Интегральная теорема Лапласа

Вероятность того, что в n независимых испытаниях, в каждом из которых некоторое событие появляется с вероятностью p , событие наступит не менее k₁ и не более k₂ раз, приближенно равна

P(n, k₁ £ k £ k₂) = (F(x₂) - F(x₁))/2, (1.24)

где

- функция Лапласа,

.

Пример 4.1. По каналу связи передается n = 6 сообщений, каждое из которых независимо от других, с вероятностью p = 0,2 оказывается искаженным. Найти вероятности следующих событий:

A = {ровно два сообщения из 6 искажены},

B = {не менее двух сообщений из 6 искажены},

C = {все сообщения будут переданы без искажений},

D = {все сообщения будут искажены}.

Решение. По формуле Бернулли (1.21)

,

P(B) = P(6,2) + P(6,3) + P(6,4) + P(6,5) + P(6,6) = 1- P(6,0) - P(6,1) =

,

, .

Пример 4.2. Вероятность появления события A за время испытаний равна 0,8. Определить вероятность того, что в 100 испытаниях событие A появится: а) 80 раз; б) не менее 75 и не более 90 раз; в) не менее 75 раз.

Решение

1) Воспользуемся локальной теоремой Муавра-Лапласа:

j(0) = 0,3989, тогда P(100,80) = 0,0997.

2) Согласно интегральной теореме Муавра-Лапласа

P(100,75<k< 90) =(F(2,5)-F(-1,25))/2=(F(2,5)+

+ F(1,25))/2.

Значение функции Лапласа определяем по таблице Лапласа F(2,5)=0,9876;

F(1,25) = 0,7888. P(100, 75<k<90)=0,8882.

1.5. Случайная величина. Закон распределения

Под случайной величиной (СВ) понимается величина, которая в результате опыта со случайным исходом принимает то или иное значение, причем, заранее до опыта неизвестно какое именно. Обозначения случайной величины: X, Y; значения случайной величины: x, y.

Случайные величины могут быть дискретными или непрерывными, а область возможных исходов может быть представлена конечным множеством, счетным или бесконечным.

Закон распределения случайной величины — любое правило, устанавливающее соответствие между значениями случайной величины и вероятностями ее наступления.

Рядом распределения дискретной СВ X называется таблица, в верхней строке которой перечислены все возможные значения СВ x₁, x₂, ..., x_n (x_i-1 < x_i), а в нижней — вероятности их появления p₁, p₂, ... , p_n , где p_i=P{X=x_i}.

x1	x2	...	xn
p1	p2	...	pn

Так как события {X=x₁}, ... ,{X=x_n} ... несовместны и образуют полную группу, то справедливо контрольное соотношение

p₁ + p₂ + ... + p_n = 1. (1.25)

Функцией распределения случайной величины X называется вероятность того, что она примет значение меньшее, чем аргумент функции x: F(x)=P{X<x}.

Свойства функции распределения:

1. F(-¥ ) = 0.

2. F(+¥ ) = 1.

3. F(x₁) £ F(x₂), при x₁ < x₂.

4. P(a £ X < b) = F(b) - F(a). (1.26)

Функция распределения дискретной случайной величины

Исходной информацией для построения функции распределения дискретной случайной величины X является ряд распределения этой СВ.

xi	x1	x2	x3	...	xn	>xn
pi	p1	p2	p3	...	pn	0
F(xi)	0	p1	p1+p2		p1+…+pn-1	1

F(x_i)=P{X<x_i}=P{(X=x₁)È(X=x₂)È ... È(X=x_i-1)}= p₁+...+p_i-1.

Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятностям этих значений.

Непрерывная случайная величина (НСВ). Плотность вероятности

Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:

P{x£ X <x+Dx}=F(x+Dx) - F(x).

Плотность вероятности на этом участке определяется отношением

. (1.27)

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок

[a, b[ равна сумме элементарных вероятностей на этом участке:

(1.28)

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

(1.29)

В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x.

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) ³ 0.

2. Условие нормировки: (1.30)

Пример 5.1. По одной и той же стартовой позиции противника производится пуск из пяти ракет, причем вероятность попадания в цель при каждом пуске одной ракеты равна 0,8. Построить ряд распределения числа попаданий.

Решение. Случайная величина X (число попаданий в цель) может принимать следующие значения: 0, 1, 2, 3, 4, 5. Найдем вероятность принятия величиной X этих значений, используя формулу Бернулли:

,

,

,

,

,

.

Ряд распределения имеет вид:

xi	0	1	2	3	4	5
pi	0,00032	0,0064	0,0512	0,2048	0,4096	0,32768

Пример 5.2. Случайная величина X распределена по закону, определяемому плотностью вероятности вида

Найти константу c, функцию распределения F(x) и вычислить P{|x| < p/4}.

Решение. Константу с вычислим исходя из условия нормировки:

,

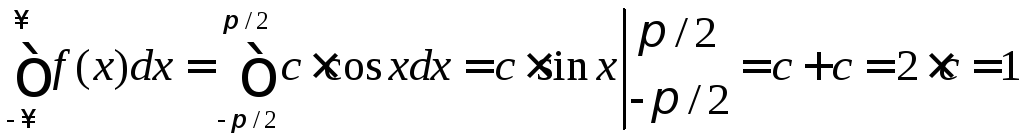откуда с = 0,5.

Так как плотность вероятности задана различными формулами на разных интервалах, то и функцию распределения будем искать для каждого интервала в отдельности.

Для x < -p/2 ,

для -p/2£x£p/2 ,

для x > p/2 .

Окончательно имеем

Вероятность P{|x| < p/4}=.