14. Несбалансированная тз

Специфика математической модели ТЗ позволяет наряду с общими методами решения задач ЛП применять специальные методы, позволяющие сократить вычисления.

Постановка задачи. Имеется m пунктов производства (складов) некоторого одного продукта, задан ai – объем производства в i-м пункте производства, . Есть n пунктов потребления этого продукта, задан bj – объем потребления (поданные заявки на поставку продукта) в j-м пункте потребления, .

Пункты производства связаны с пунктами потребления сетью дорог с определенными тарифами на перевозки. Стоимость перевозки одной единицы продукта (груза) из i –го пункта производства в j-ый пункт потребления равна с_ij. Необходимо найти оптимальный план перевозок продукции, при котором транспортные издержки минимальны, продукция полностью вывозится из пунктов производства и полностью удовлетворяется потребность в продукции.

Модель. В качестве переменных выбираются элементы матрицы перевозок: .  

Пусть  – количество единиц продукции, вывозимых из i-го пункта производства в j-й пункт потребления.

 

                       

 

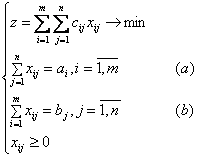
Ограничения группы (a) задают условие: из каждого i-го пункта производства должен быть вывезен весь продукт. Например (рис. 3.1), из первого пункта производства с объемом производства a1  продукт может быть перевезен в любой пункт потребления. Объемы перевозок неизвестны и составляют: – количество единиц продукции, перевезенных из первого пункта производства в первый пукнт потебления; – количество единиц продукции, перевезенных из первого пункта производства во второй пункт потребления; – количество единиц продукции, перевезенных из первого пункта производства в n-ый пункт потребления. Сумма всех перевезенных единиц продукции должна быть равна a₁. Получаем ограничение:

.

Ограничения группы (b) задают условие: в каждый j-й пункт потребления завезен весь необходимый продукт. 

Размерность задачи: . Транспортная задача – частный случай задачи линейного программирования, в которой все ограничения представлены равенствами. В отличие от общего случая решения задачи ЛП оптимальное решение транспортной задачи всегда существует.

 

Открытая и закрытая транспортные задачи. Выделяют два типа ТЗ:  открытая ТЗ и закрытая ТЗ.

Транспортная задача называется закрытой, если выполняется условие баланса : суммарный объем производства равен суммарному объему потребления:

.                                        (3.1)

Следнет обратить внимание на то, что математическая модель задает закрытую транспортную задачу. 

Открытая ТЗ имеет место в двух случаях.

Первый случай. Суммарный объем производства меньше суммарного объема потребления:

.                                      (3.2)

Известно, что для существования допустимого решения транспортной задачи необходимо и достаточно, чтобы задача была закрытой. Поэтому транспортную задачу открытого типа предварительно необходимо свести к закрытой, для чего вводится фиктивный пункт производства с номером m+1 с объемом производства:

,                              (3.3)

при этом полагают .

Второй случай. Суммарный объем производства больше суммарного объема потребления:

.                                     (3.4)

Для сведения ТЗ к закрытому типу вводят фиктивный пункт потребления с номером n+1 с объемом потребления:

,                               (3.5)

при этом полагают .

Методы решения.

     Как задача линейного программирования ТЗ может быть решена симплекс методом [4].

     Также разработаны специальные (более эффективные) методы решения транспортной задачи: обобщенный венгерский метод [4]; метод северо-западного угла, метод минимального элемента для нахождения опорного плана; метод потенциалов для нахождения оптимального плана [3].