25. Градиентные методы

Во многих алгоритмах многомерной оптимизации так или иначе используется информация о градиентах. Проиллюстри­руем это положение следующим простым примером. Представим себе, что альпинисту завязали глаза и сказали, что он должен добраться до вершины «унимодальной» горы. Даже ничего не видя, он может это сделать, если все время будет двигаться вверх. Хотя любая ведущая вверх тропа в конечном счете при­ведет его к вершине, кратчайшей из них будет самая крутая, если, правда, альпинист не натолкнется на вертикальный обрыв, который придется обходить. (Математическим эквивалентом об­рыва на поверхности, образуемой целевой функцией, являются те ее места, где поставлены условные ограничения.) Предположим пока, что задача оптимизации не содержит ограничений. Позднее мы включим их в схему поиска. Метод оптимизации, в основу которого положена идея движения по самой крутой тропе, на­зывается методом наискорейшего подъема или наискорейшего спуска. Вектор градиента перпендикулярен линии уровня и указывает направление к новой точке в пространстве проектиро­вания. Отметим, что градиентный метод в отличие от метода ка­сательной к линии уровня можно использовать применительно к любой унимодальной функции, а не только тех, у которых это свойство явно выражено.

Чтобы лучше понять идею градиентных методов, подробнее остановимся на свойствах градиентов. Рассмотрим систему неза­висимых единичных векторов е₁, е₂, е₃, . ., e_N, направленных вдоль осей координат x₁ , х₂ , х₃ , . . ., x_N , являющихся в то же время: проектными параметрами. Вектор градиента произвольной целевой функции F(х₁, х₂, х₃ , . . ., х_N ) имеет вид

где частные производные вычисляются в рассматриваемой точке. Этот вектор направлен вверх, в направлении подъема; обратный: ему вектор указывает направление спуска. Единичный вектор градиента часто представляют в виде .

где

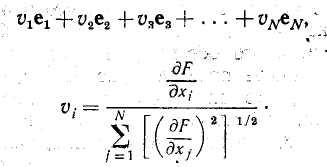
Иногда характер целевой функции бывает достаточно хорошо известен, чтобы можно было вычислить компоненты вектора градиента путем непосредственного дифференцирования. Если таким способом частные производные получить не удается, то можно найти их приближенные значения в непосредственной. окрестности рассматриваемой точки: .

Здесь  — небольшое смещение в направлении х_j. Эту формулу часто называют «приближением секущей». Полученную информацию о направлении градиента можно использовать различным образом для построения алгоритма поиска.

Ступенчатый наискорейший подъем

Ряд методов поиска основан на смещении на постоянный шаг в направлении градиента с последующим вычислением целевой функции. Если ее величина оказывается больше предыдущей, вычисляется градиент в новой точке, и вся процедура повторяется, причем часто при этом шаг увеличивают. Если же величина целевой функции не изменяется или убывает, то шаг смещения от предыдущей точки уменьшают и повторяют всю процедуру вычислении. Так поступают до тех пор, пока дальнейшее уменьшение шага уже не приводит к улучшению результата.

Наискорейший подъем с использованием одномерного поиска

В некоторых методах поиска информация о градиенте используется для ведения одномерного поиска в направлении наискорейшего подъема или спуска, причем используется соотношение

х_i.нов =х_i.ст + Sv_i

где S — новый одномерный параметр, значения которого отсчитываются в направлении градиента. Получив одномерный оптимум в направлении данного градиента, находят новый градиент и повторяют процесс до тех пор, пока последующие вычисления позволяют улучшать полученный результат. Главное достоинство этого метода состоит в том, что параметр S можно использовать в качестве независимой переменной для поиска по методу Фибоначчи, и это обеспечивает высокую эффективность метода. Другое важное преимущество рассматриваемых мето­дов состоит в том, что они позволяют уходить от седловых точек поверхности, описываемой целевой функцией (рис. 7.5). Отметим, однако, что, как видно из рисунка, для мультимодальных функций градиентные методы позволяют найти лишь локальный оптимум. Поэтому, если характер поверхности недоста­точно хорошо известен, следует испробовать несколько исходных точек и убедиться, что во всех случаях получается одно и то же оптимальное решение. Другой причиной, снижающей эффективность градиентных методов, являются изломы линий уровня целевой функции. Так как такие точки соответствуют разрыву в наклоне линий контура, то здесь возможны ошибки в определении направления дальнейшего поиска. Поэтому поиск может замедлиться и идти зигзагами поперек линии излома, а время, необходимое для получения решения, будет столь велико, что счет придется прекратить. В действительности боль­шинство исследуемых поверхностей имеет одну или более линий излома, которые нередко проходят через точку оптимума. Поэтому, наткнувшись на линию излома, следует в дальнейшем

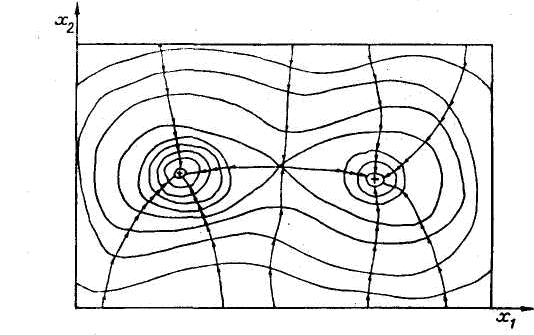
Рис. 6.5 Бимодальная целевая функция

двигаться вдоль нее. Для реализации этой идеи разработан ряд остроумных алгоритмов. Ниже рассмотрим некоторые из них, а также другие «безградиентные» методы, хорошо приспособлен­ные для поиска оптимумов функций с разрывными производ­ными.

6.5. Метод Флетчера-Ривса

Этот метод позволяет найти минимум нелинейной целевой функции многих переменных вида

M=F(x₁ , x₂, . . ., x_N)

при отсутствии ограничений. Метод основан на применении частных производных целевой функции по независимым переменным и предназначен для исследования унимодальных функций. С его помощью можно исследовать и мультимодальные функции, однако в этом случае следует брать несколько исходных точек и проверять, одинаково ли во всех случаях решение. Схема алгоритма метода Флетчера — Ривса представлена на рис. 7.6. Выполняется он следующим образом. Сначала выбирается под-

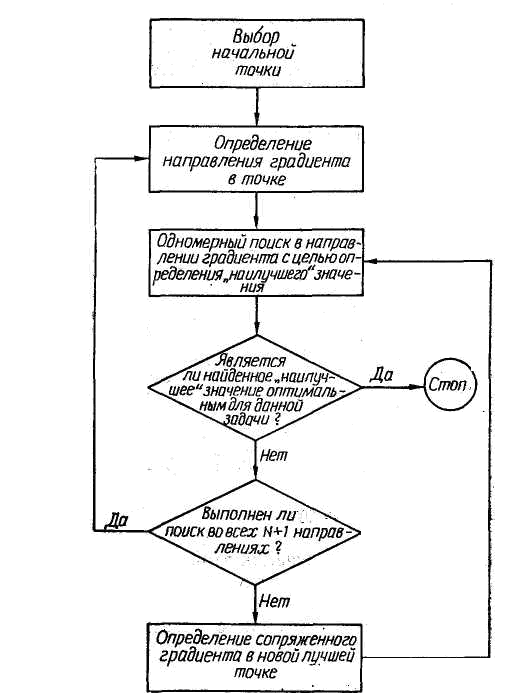
Рис. 6.6 Блок-схема алгоритма метода Флетчера – Ривса

ходящая начальная точка пространства проектирования и путем вычисления компонент вектора градиента

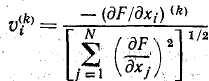
определяется направление наискорейшего спуска. Индекс k=1 соответствует исходной точке. Затем в направлении наискорейшего спуска ведется одномерный поиск по формуле

х_i.нов = х_i.ст + Sv_i , i=1,2, ...,N,

где S — смещение в направлении вектора градиента. Найдя минимум в этом направлении, определяют направления новых единичных векторов, которые несколько отличаются от направления нового вектора градиента и представляют собой линейные комбинации вектора градиента на данном шаге и вектора градиента, полученного на предыдущем шаге. Новые компоненты единичных векторов выражаются в виде

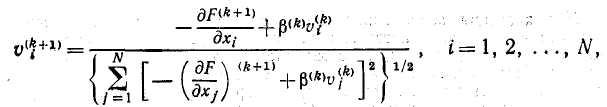
где

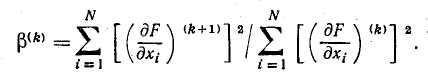
Индекс k указывает на последовательность вычислений в процессе итераций. Новые направления называются «сопряженными» и соответствуют текущей локальной квадратичной аппроксимации функции. Затем по новому направлению проводят одномерный поиск и, найдя минимум, проверяют, достигнута ли требуемая степень сходимости. Если проверка показывает, что это так, то счет прекращается. В противном случае определяют новые сопряженные направления, k увеличивают на единицу и продолжают процесс до тех пор, пока не будет обеспечена сходимость или пока поиск не будет проведен по всем N+1 направлениям. Закончив цикл поиска по N+1 направлениям, начинают новый цикл, в котором опять используется направление наискорейшего спуска. Достоинство этого алгоритма состоит в том, что он позволяет использовать преимущества градиентных методов, проявляющиеся при исследовании целевой функции с разрывными производными. Так как N+1 направлений поиска второй совокупности отличаются от направлений единичных векторов градиента, то поиск не «зависает на изломе», а идет вдоль линии, соединяющей точки изломов линии уровня, которая, как правило, проходит через точку оптимума. Вообще можно утверждать, что методы, основанные на определении новых направлений поиска на основе накопленных данных о локальном поведении функции, по самой своей природе более эффективны, чем методы, в которых направление поиска задается заранее. Именно поэтому метод Флетчера — Ривса обладает большими преимуществами по сравнению с методами наискорейшего спуска или подъема. Его недостаток состоит в том, что, будучи сложнее указанных методов, он требует разработки более сложных программ.

6.6. Метод Дэвидона-Флетчера-Ривса

Метод Дэвидона — Флетчера — Пауэлла представляет собой алгоритм оптимизации, приспособленный для отыскания безусловного минимума целевой функции, зависящей от нескольких переменных и имеющей вид

M=F(x₁ , x₂ , ..., x_N).

Необходимы частные производные целевой функции по независимым переменным. Поскольку в основе метода лежит допуще­ние об унимодальности целевой функции, в тех случаях, когда есть основания предполагать, что она не является таковой, следует брать несколько исходных точек. На рис. 6.7 представлена схема алгоритма метода Дэвидона — Флетчера — Пауэлла. Алгоритм выполняется следующим образом. Сначала в пространстве проектирования выбирают подходящую начальную точку. Затем, вычисляя составляющие вектора градиента

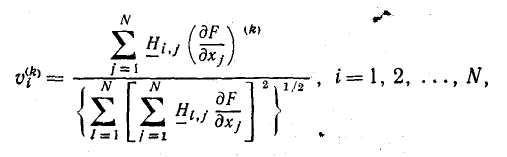
определяют направление поиска. Здесь k —номер итерации, а Н_i,j — элементы симметричной положительно определенной матрицы размерности NxN. В процессе итераций эта матрица превращается в матрицу, обратную матрице Гессе, элементами

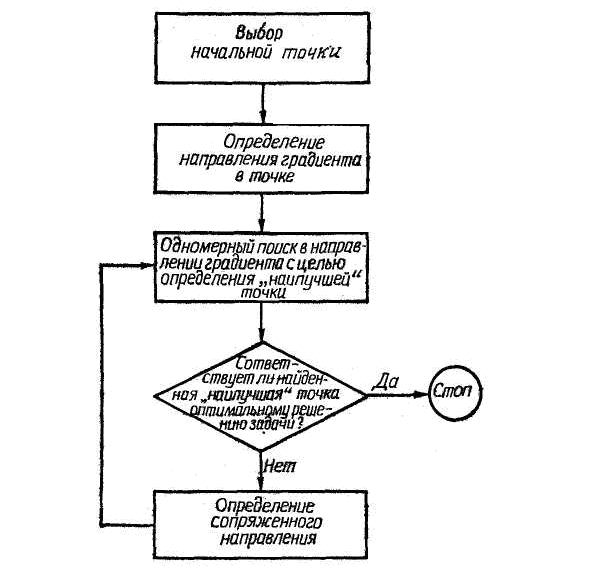
Рис. 6.7 Блок-схема алгоритма метода Дэвидона – Флетчера – Пауэлла

которой являются вторые частные производные целевой функции. Поскольку обычно матрица заранее неизвестна, то в качестве начальной можно воспользоваться любой симметричной положительно определенной матрицей. Как правило, берут простейшую из них — единичную матрицу. В этом случае поиск начинается вдоль линии наискорейшего спуска. Одномерный поиск ведется вдоль исходного направления в соответствии с соотношением

х_i.нов = х_i.ст + Sv_i , i=1,2, ...,N,

где S — величина шага в направлении поиска. Найдя одномерный оптимум, проверяют результат на сходимость и, если она достигнута, поиск прекращают. В противном случае для дальнейшего поиска выбирают новое направление, причем используют прежнее соотношение и новую матрицу, определяемую формулой

Элементы матриц А^(k) и B^(k), имеющих размерность NxN, вычисляются по формулам

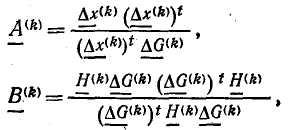
где верхним индексом t обозначены транспонированные матрицы, a x^(k) и G^(k) — соответственно векторы-столбцы разностей значений х_i и градиентов в двух точках. Векторы-столбцы определяются выражениями

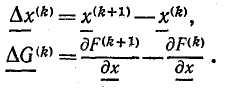
В соответствии с правилами матричного исчисления числители выражений для. А^(k) и В^(k) представляют собой матрицы размерности NxN, а знаменатели являются скалярами. Определив новое направление поиска, проводят одномерный поиск и продолжают итерационный процесс. При выполнении описываемого алгоритма поиск после первой попытки ведется в тех направлениях, в которых целевая функция в ближайшей окрестности имеет значения, приближающиеся к оптимальному. Лишь в редких случаях эти направления совпадают с направлением градиента. Поэтому данный алгоритм часто называют методом «отклоненного» градиента. Указанное свойство метода Дэвидона — Флетчера — Пауэлла позволяет обходить трудности, связанные с разрывами производных в пространстве проектирования. Широко распространено мнение, что этот метод является наиболее эффективным из всех градиентных методов. В отличие от метода Флетчера — Ривса он дает полную информацию о кривизне поверхности целевой функции в точке минимума, однако при этом требуется больший объем памяти и большее время счета для обработки матрицы Н.

6.7. Метод конфигураций Хука-Дживса

Этот метод облегчает поиск и не требует вычисления производных. Поиск ведется вдоль линий разрыва производных в предположении, что смещения в пространстве проектирования, оказавшиеся удачными на ранней стадии поиска, могут привести к успеху и на его более поздних стадиях. Метод Хука — Дживса предназначен для отыскания минимума унимодальной функции многих переменных

M=F(х₁ , x₂ . . ., x_N)

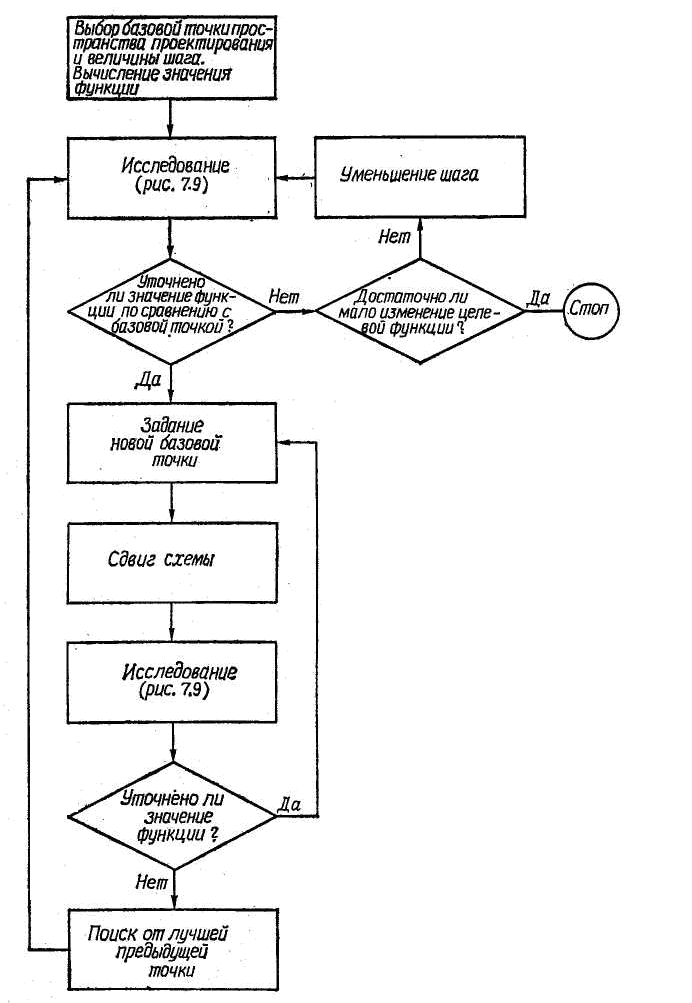
Рис. 6.8 Блок-схема алгоритма метода конфигураций Хука – Дживса

при отсутствии ограничений. На рис. 6.8 представлена схема алгоритма этого метода. Выполняется он следующим образом. Сначала выбирается исходная базовая точка пространства проектирования и величины шагов, которые будут использованы при исследовании функции. Затем в соответствии со схемой рис. 6.9 проводится исследование с заданными приращениями в направлениях, соответствующих всем независимым переменным. Там, где получено уточненное значение функции, помещают новую временную базовую точку. Закончив этап исследования, выбирают новую базовую точку и производят «сдвиг схемы». Эта операция заключается в экстраполяции вдоль линии, сое­диняющей новую и прежнюю базовые точки. Расстояние сдвига за новую базовую точку несколько превышает расстояние между двумя прежними базовыми точками. Математически экстраполяция определяется формулой

где — новая временная базовая точка, или «точка ро­ста», i — переменный индекс, k — порядковый номер стадии поиска, а а — коэффициент усиления, который больше или равен единице. Затем исследуют окрестность новой временной базовой точки, чтобы выяснить, не содержит ли она точку, приняв которую за следующую базовую можно приблизиться к оптимальному решению. Этот поиск также ведется по схеме, показанной на рис. 7.9. Если найденная временная точка роста или одна из соседних с ней точек имеет преимущество перед другими, то вся процедура повторяется с использованием ее в качестве базовой. Благодаря введению коэффициента усиления, каждое последующее исследование окрестности точки осуществ­ляется на все большем и большем удалении от исходной точки до тех пор, пока в процессе поиска не окажется пройденным пик или линия разрыва производной. В этом случае возвращаются к предыдущей «лучшей базовой точке», сужают область исследования и повторяют весь процесс снова. Если последовательно уменьшаемый шаг оказывается меньше некоторой заранее заданной величины и при этом отсутствует заметное изменение значения целевой функции, поиск прекращается. После нескольких изменений направления поиска метод Хука — Дживса обеспечивает совпадение распределения расчетных точек с линией разрыва производных. Обычно после завершения выбора схемы поиска сдвиг на каждом следующем шаге увеличивается, пока не превысит величину исходного шага в 10 или даже в 100 раз. Поэтому в случае, когда сдвиг оказывается неудачным, единственный способ продолжить поиск — вернуться к наиболее удачной из базовых точек и начать все сначала. Тот факт, что данный алгоритм обладает свойством

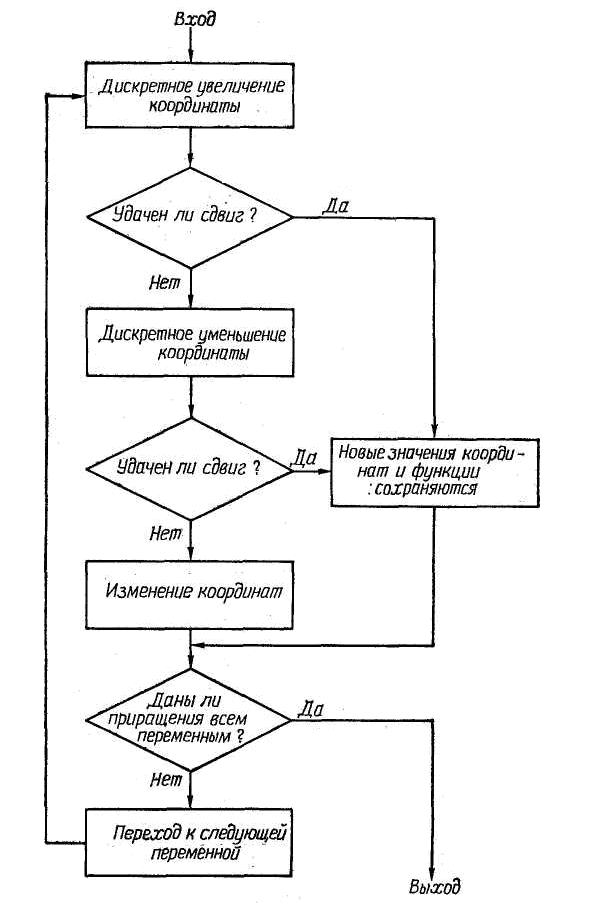
Рис. 6.9 Метод исследования, применяемый в алгоритме Хука – Дживса

«ускоряться», способствует повышению его общей эффективности. Другое достоинство метода Хука — Дживса — возможность получения с его помощью приближенного решения, качество которого непрерывно повышается на всех стадиях численного решения. Особенно явно преимущества подобных методов про­являются при отыскании экстремумов на гиперповерхностях, содержащих глубокие узкие впадины, т. е. в тех случаях, когда градиентные методы неэффективны.

6.8. Метод конфигураций Розенброка

Метод конфигураций Розенброка основан на поиске минимума вдоль линий разрыва производных и часто оказывается эффективным, когда другие методы не позволяют получить решение. Его нередко называют «методом вращения осей координат», поскольку исследование в окрестности выбранной точки ведется именно таким способом. В отличие от предыдущих методов, в которых исходным переменным сообщают независимые приращения, в методе Розенброка система координат поворачивается так, чтобы одна из осей была направлена вдоль линии разрыва производных, положение которой определяется в результате предварительного исследования. Остальные оси образуют с ней ортогональную систему координат. Метод Розенброка основан на предположении об унимодальности целевой функции и предназначен для отыскания минимума функции многих переменных вида

M=F(x₁ , x₂ , ... , x_N)

при отсутствии ограничений. На рис. 7.10 показана схема алгоритма, используемого в этом методе. Выполняется он следующим образом. Сначала выбирают начальную точку, задают начальные величины шагов S_i (i=1, 2, . . ., N) и вычисляют целевую функ­цию. Затем каждой переменной x_i сообщают приращение S_i в направлении, параллельном соответствующей оси координат в пространстве проектирования, и вновь вычисляют целевую функцию F. Если ее новое значение оказывается меньше преды­дущего, то сдвиг считается удачным и следующий шаг увеличивается в соответствии с формулой

S_i= S_i.

где ALFA>1. Если же новое значение F оказывается больше предыдущего, то сдвиг считается неудачным и следующий шаг определяется по формуле

S_i=- S_i

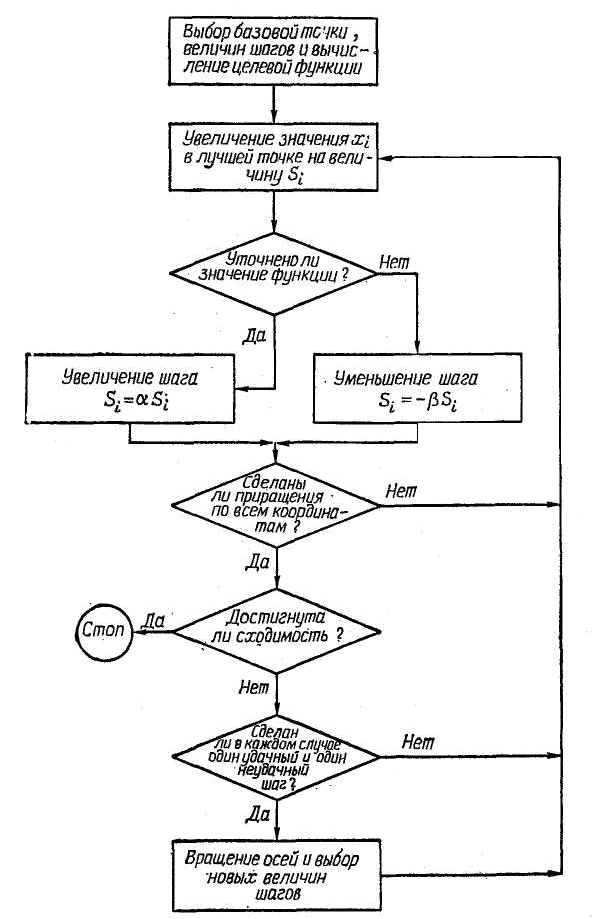
Рис. 6.10 Блок-схема алгоритма метода конфигураций Розенброка

где <1. Осуществив сдвиг по всем переменным, проверяют сходимость и, если она достигнута, поиск прекращают. В противном случае вводят дополнительную проверку, чтобы выяснить, были ли сделаны хотя бы один успешный и один безуспешный сдвиг в каждом направлении. Если такого сочетания сдвигов не было, вся процедура повторяется, начиная с первой переменной. Если же подобное сочетание обнаружено для каждого направления, оси поворачивают так, чтобы исходное направление поиска совпало с наиболее перспективным из ранее рассмотренных направлений. Затем выбирают новые значения шагов и продолжают поиск по всем переменным, пользуясь новой системой координат. В отличие от других, данный алгоритм нацелен на отыскание оптимальной точки в каждом направлении, а не просто на фиксированный сдвиг по всем направлениям. Величина шага в процессе поиска непрерывно изменяется в зависимости от конфигурации рельефа поверхности. Сочетание вращения вектора, направленного вдоль линии разрыва производных, с регулированием масштаба делает метод Розенброка исключительно эффективным при решении сложных задач оптимизации.