26. Метод квадратичной аппроксимации
Метод квадратичной аппроксимации относится к семейству методов полиномиальной аппроксимации. Идея метода полиномиальной аппроксимации состоит в том, что в некоторой окрестности минимума функции Ф(х) она аппроксимируется полиномом достаточно высокого порядка и в качестве точки минимума функции Ф(х) (или в качестве очередного приближения к этой точке) принимается точка минимума аппроксимирующего полинома. В силу того, что аппроксимирующая функция является полиномом, этот минимум находится легко.
В качестве аппроксимирующих полиномов чаще всего используются полиномы второго и третьего порядков, т.е. квадратичная и кубическая аппроксимации.
Квадратичная аппроксимация.
Рассмотрим квадратичную аппроксимацию (см. рис. 1). Пусть в процессе решения задачи поиска минимума функции Ф(х) тем или иным образом получены попарно не совпадающие точки х1,х2,х3, принадлежащие области допустимых значений D (не обязательно упорядоченные слева направо!).
Построим квадратичную функцию
(1)
проходящую
через точки
,
,
где
.
Коэффициенты ,α,β ,γ функции (1) удовлетворяют системе линейных алгебраических уравнений (СЛАУ)
(2)
Определитель СЛАУ (2) является определителем Вандермонда, который отличен от нуля, если величины ,х1,х2,х3, попарно различны.
Таким
образом, в сделанных предположениях
СЛАУ (2) имеет решение и, притом единственное.
Поскольку определитель СЛАУ (2) равен
, это решение имеет вид
где
,
,
.
Подставим
найденные значения коэффициентов
,α,β,γ, в необходимое условие
=0
минимума квадратичной функции (1), получим
стационарную точку этой функции
(3)
где
Рассмотрим следующую задачу условной оптимизации: найти минимум одномерной унимодальной функции Ф(х), определенной в замкнутой области допустимых значений D=[а,b],
(4)
Метод
квадратичной аппроксимации относится
к классу методов сокращения текущего
интервала неопределенности. Пусть при
решении задачи (4) каким-либо методом
получены три точки
,
принадлежащие области допустимых
значений, такие, что
.
Схема метода квадратичной аппроксимации:
Выполняем присваивания r=1,
,
,
,
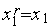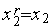.Вычисляем значения
,
функции Ф(х) в точках
, соответственно.По формуле (3) вычисляем величину
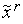и
находим значение функции Ф(х) в этой
точке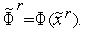
.Находим следующие три точки:
случай
(а) – если
[
,
],
то
=
,
=
,
=
.(см.
рис. 2);
случай
(б) – если
[
,
],
то
=
,
=
,
=
(см.
рис. 3).
В качестве следующего текущего интервала неопределенности принимаем
Если
,
то заканчиваем вычисления. Иначе -
выполняем присваиваниеr=r+1
и переходим на п.2. Здесь
–
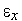требуемая точность решения.
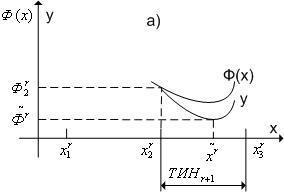Рис.
2. К методу квадратичной аппроксимации
(случай а).
Рис.
3. К методу квадратичной аппроксимации
(случай б).
В
качестве приближенного значения точки
минимума
с
равными основаниями может быть принята
любая точка последнего текущего интервала
неопределенности.
Замечание.
В силу условий
,
точка
всегда
принадлежит текущему интервалу
неопределенности ТИНr=[
,
].
27. Метод кубической аппроксимации
Функция 
аппроксимируется полиномом
третьего порядка. Находится стационарная
точка 
этого
полинома. Эта точка заключается в
интервал 
такой,
производные в 
|
имеют разные знаки.
Построим полином
находятся
так, чтобы значения функции и значения
производной были: 
и 
,
и совпадали бы с 
и 
соответственно
в точках 
и 
.
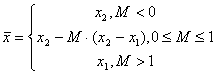
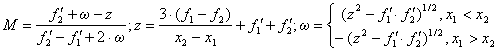
Формула
для 
обеспечивает
надлежащий выбор одного из двух корней
квадратного уравнения.
Для
значений 
,
заключённых в интервале от 0 до 1 формула
для 
гарантирует,
что 
всегда
будет между 
и 
.
Алгоритм
1.
Задать 
–
начальное приближение, 
-
шаг поиска и 
погрешности
по функции и аргументу.
2.
Вычислить 
в 
.
Если 
,
то 
и 
,
иначе 
и
какая-нибудь своя формула для
вычисления 
. 
3.
Вычислять 
до
тех пор, пока не получим 
в
которой 
.
Вычислить 
.
4.
Вычислить 
(см.
выше).
5.
Если 
,
то перейти к п. 6 иначе 
и
так вычислять, пока не выполнится
условие 
.
6.
Проверка на окончание 
и 
.
Если выполняется, то конец вычислений,
иначе если 
,то 
или,
если 
,то 
и
перейти к п. 4.