Занятие 7. Исследование зависимости признаков методом корреляционного анализа. Коэффициент корреляции. Корреляционное отношение

Задачи обработки геоданных, решаемые на основе корреляционного анализа:

1. изучение зависимостей между анализируемыми признаками (например, между различными физическими свойствами горных пород), между показаниями различных методов (например, между глубиной залегания сейсмического горизонта и аномальными значениями силы тяжести в гравиразведке) и т. д.;

2. аппроксимация некоторой зависимостью, в частности, полиномами заданной степени.

Изучение и построение указанных зависимостей предусматривают оценку тесноты связи и формы проявления этой связи.

Зависимость, при которой изменение одной величины вызывает изменение распределения другой, называется статистической(стохастической). При статистической зависимости различаюткорреляцию, когда устанавливают существование взаимосвязи между двумя (или более) случайными величинами и оценивают силу (тесноту) этой связи, ирегрессию, когда выясняют характер (форму) зависимости между величинамиXиYи возможность оценкиYпоX(илиXпоY), причем либоX, либоY, либоXиYявляются случайными величинами.

Оценка тесноты связи производится с помощью коэффициента корреляции, корреляционного отношения, коэффициента ранговой корреляции, множественного коэффициента корреляции, частного коэффициента корреляции.

7.1. Коэффициент корреляции как измеритель степени тесноты связи

Для изучения характера и структуры статистических взаимосвязей между компонентами анализируемого многомерного признака ξ = (,,…,),p> 2, используется нормированная ковариационная матрица, называемаякорреляционной:

R = (), (7.1)

где элементы получаются из элементов матрицы ковариацийс помощью нормировки

= / ()^1/2. (7.2)

Характеристики называютсякоэффициентами корреляциимежду случайными величинамиии определяютстепень тесноты линейной статистической связимежду этими признаками и обладают следующими свойствами:

1. абсолютная величина 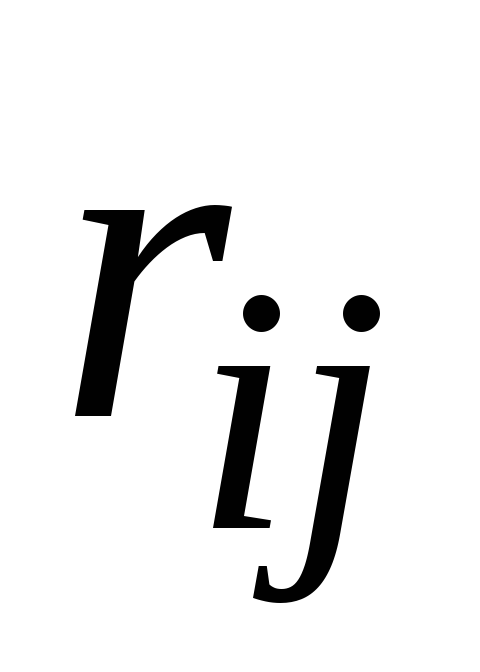не превосходит единицы –1 ≤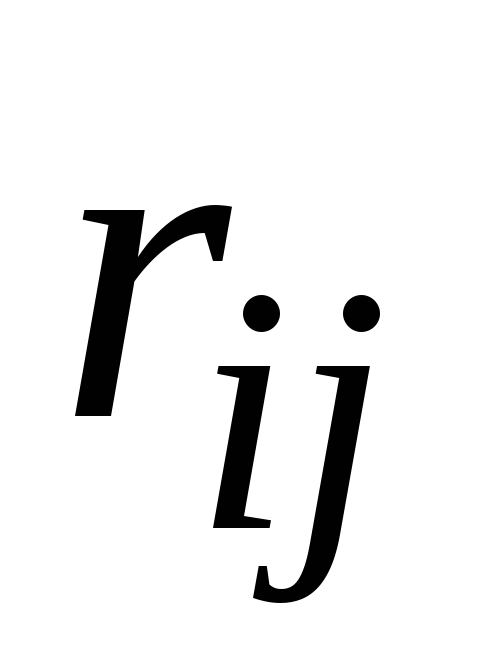≤ 1;

2. максимальная степень тесноты связи соответствует значениям коэффициента корреляции, равным +1 или –1, и достигается либо при измерении связи признака с самим собой, либо при наличии линейной функциональной связи между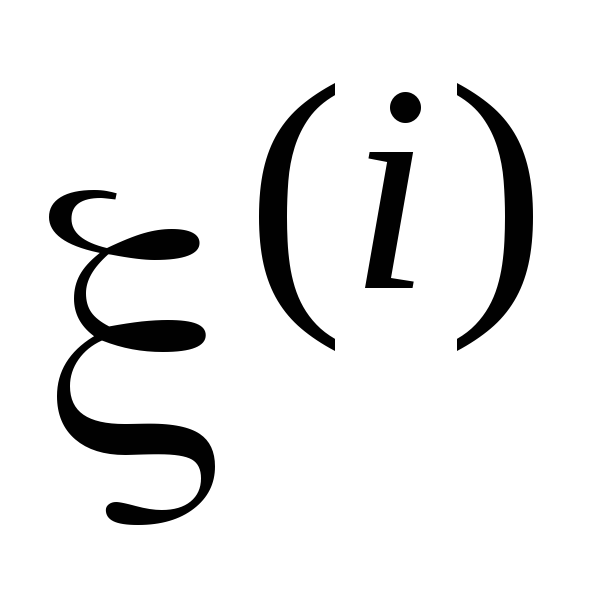и, т. е. в случае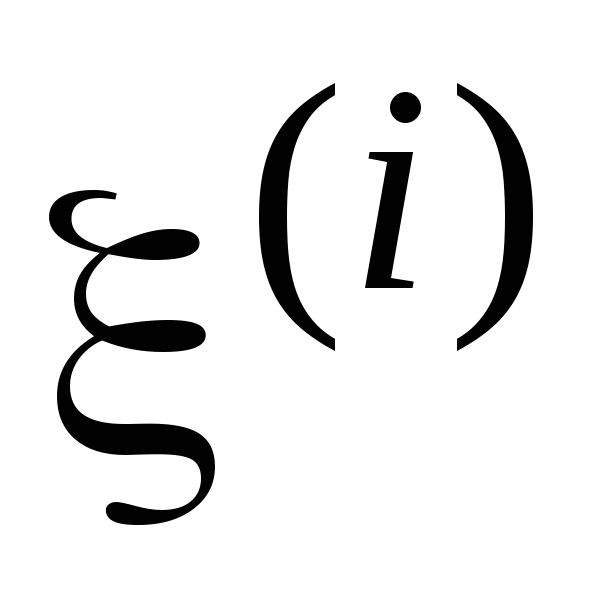=b₀+b₁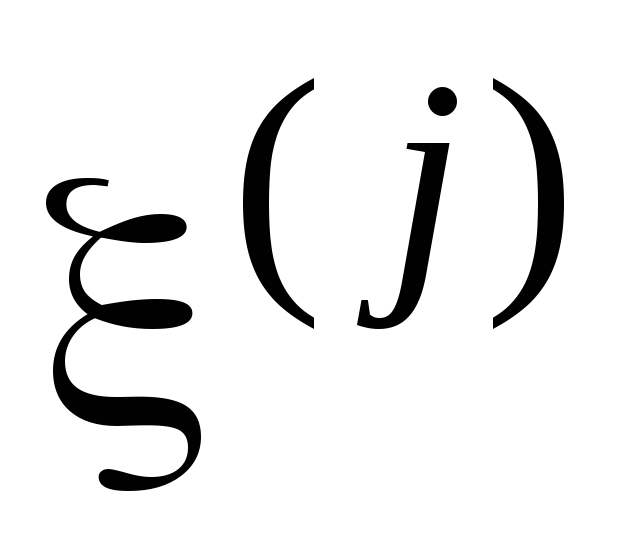, гдеb₀ иb₁ – некоторые постоянные величины; еслиb₁ > 0, то связь называетсяположительной, а еслиb₁ < 0, то связь называетсяотрицательной.Положительность коэффициента корреляцииrозначает одинаковый характер тенденции взаимосвязанного изменения случайных величин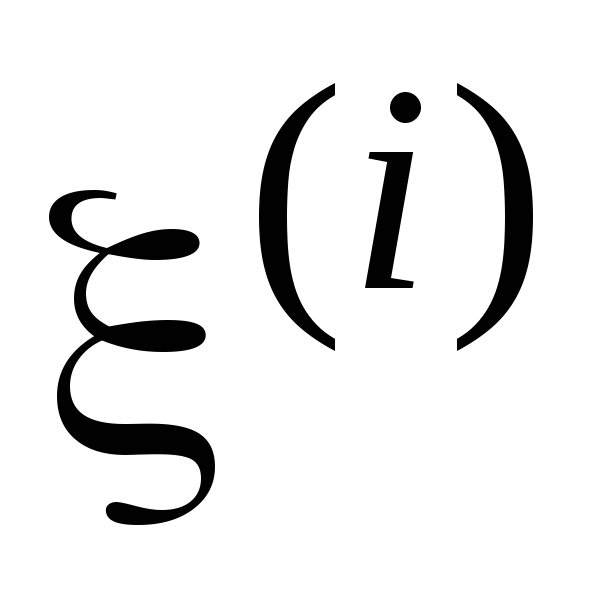и. Отрицательное значениеrговорит о противоположной тенденции взаимосвязанного изменения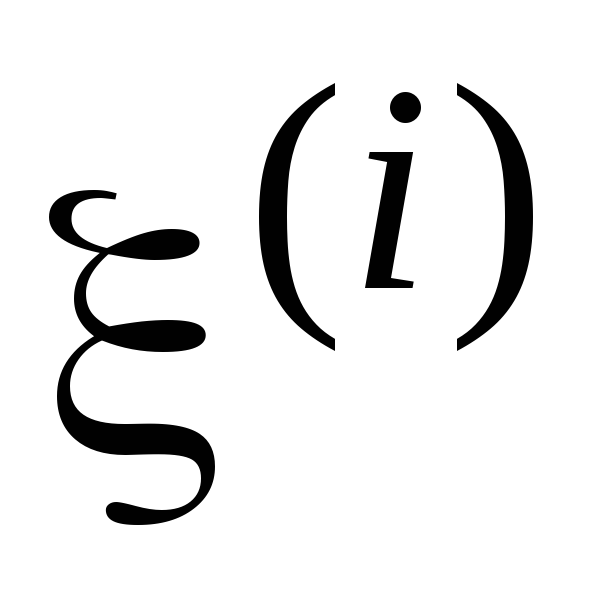и;

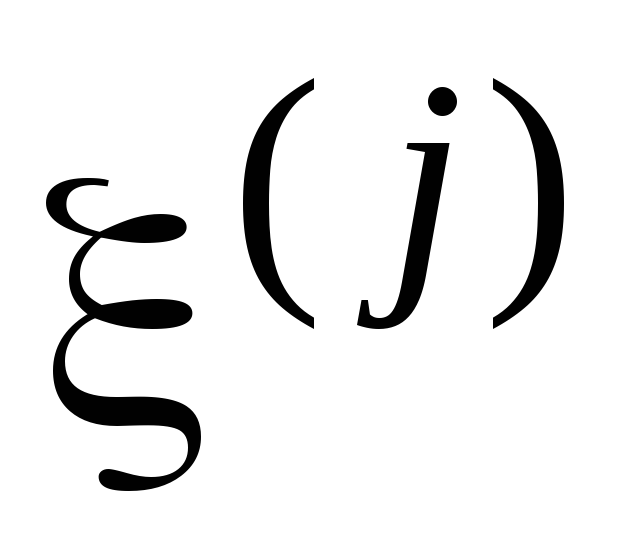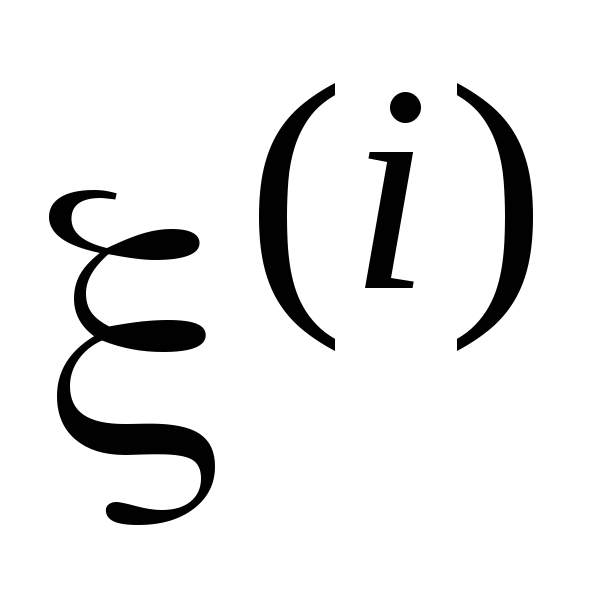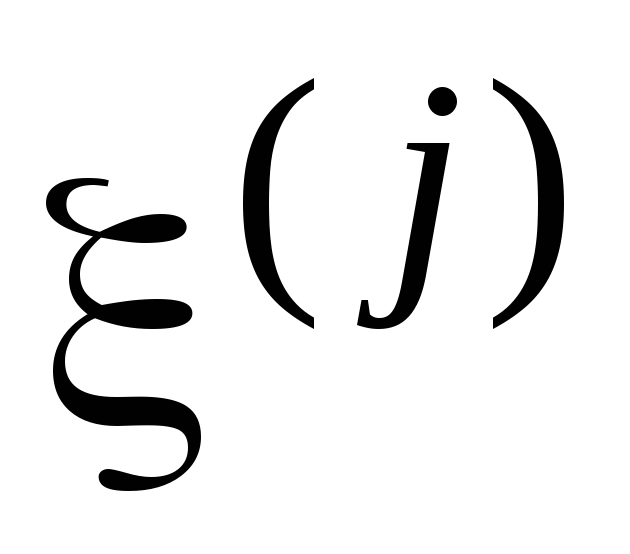3. если случайные компоненты истатистически независимы, то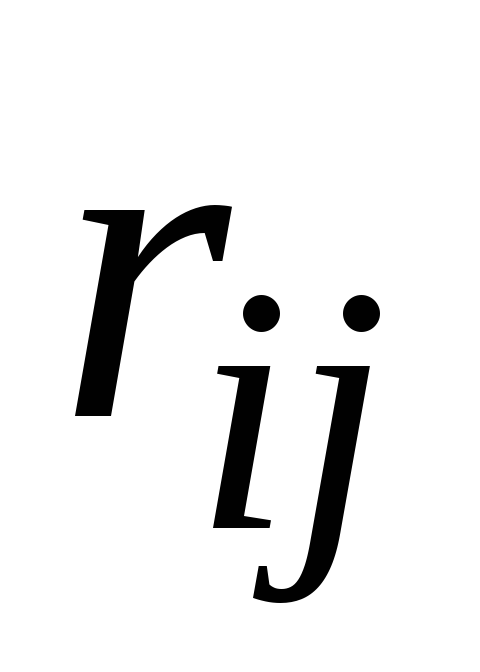= 0. Обратное утверждение (из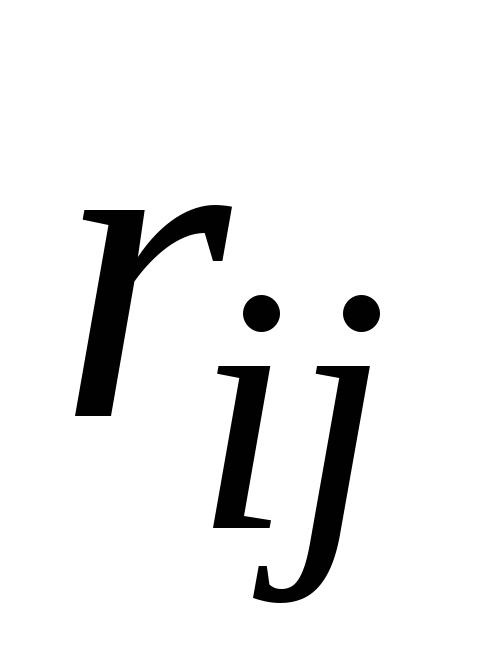= 0 следует независимость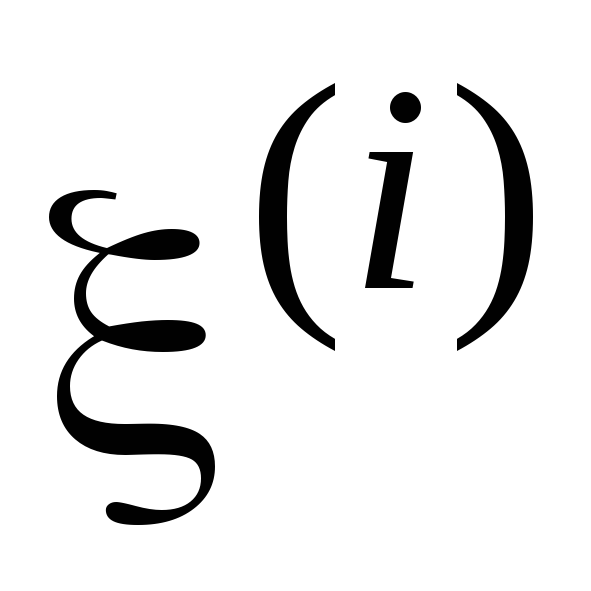и) верно лишь для некоторых частных случаев (например, для нормально распределенных пар (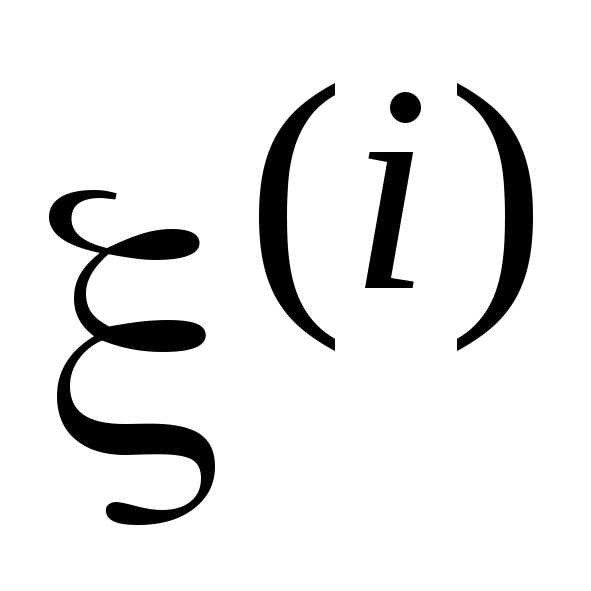,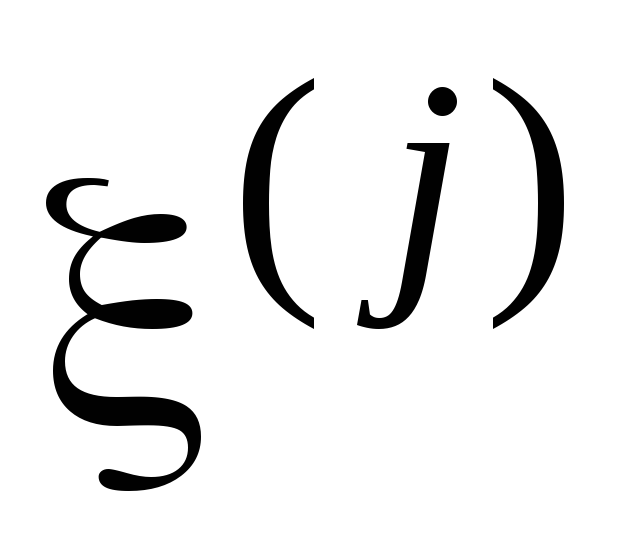) иневерно в общем случае.

Выборочное значение коэффициента корреляции (т. е. статистическая оценка неизвестного значенияr) подсчитывается по исходным статистическим данным (x₁, y₁), (x₂, y₂),…, (x_n, y_n) по формуле

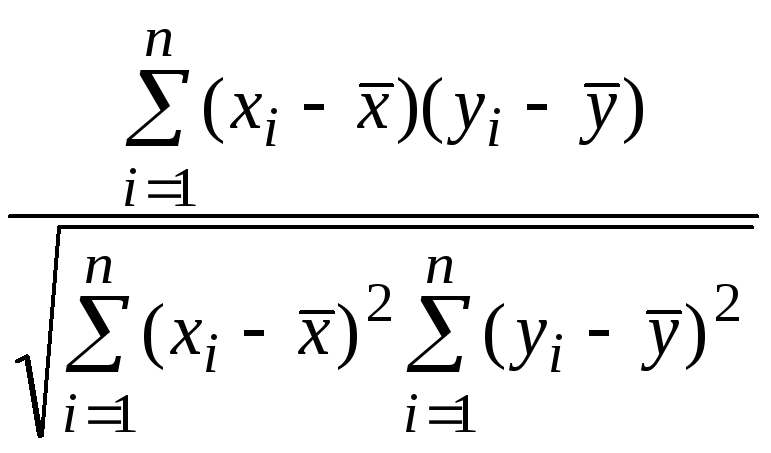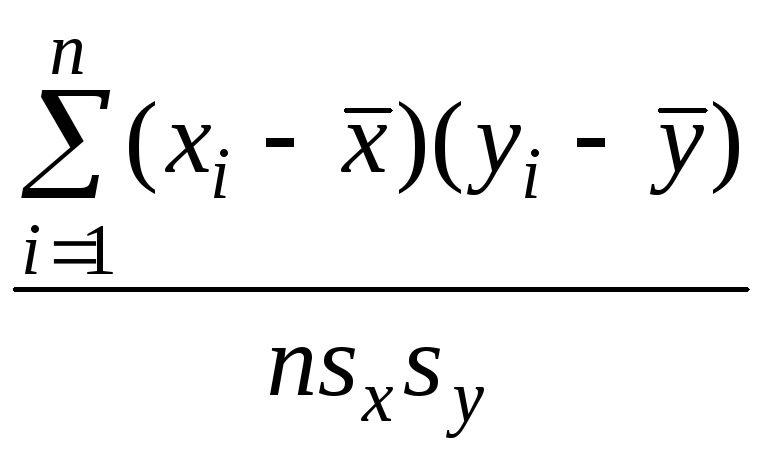= =, (7.3)

где и– оценки средних значенийx и y, ,–оценки стандартных отклонений x и y.

. Теоретический и выборочный коэффициенты корреляции, определенные соотношениями (7.2) и (7.3) соответственно, могут быть формально вычислены для любой двумерной системы наблюдений. Они являются измерителями степени тесноты линейной статистической связи между анализируемыми признаками. Однако только в случае совместного нормального распределения исследуемых случайных величин ξ и η коэффициент корреляции r имеет смысл как характеристика степени тесноты связи между ними.

7.2. Распределение выборочного коэффициента корреляции и проверка гипотезы о статистической значимости линейной связи

В случае совместной нормальной распределенности исследуемых переменных и при достаточно большом объеме выборки праспределениеможно считать приближенно нормальным со средним, равным своему теоретическому значениюrи дисперсией.. Способ проверки гипотез, связанных с коэффициентом корреляции, зависит от объема выборки и теоретического значения этого коэффициента.

Случай малых значенийи большихп. Для проверки гипотезы об отсутствии корреляционной связи между исследуемыми переменнымиН₀ :r = 0 при малых значениях ‌r‌ и большихписпользуется тот факт, что величинаt =при справедливостиН₀имеет распределение Стьюдента сп­– 2 степенями свободы.