8. Формула Мотта. Форм-фактор. Распределение заряда в ядре.

Рассмотрим упругое рассеяние электронов на ядре и покажем, как из экспериментальных данных можно извлечь сведения о пространственной структуре ядра-мишени. Упругое рассеяние означает, что не происходит изменения внутреннего состояния ядра после рассеяния. Оно не возбуждается. Прежде всего рассмотрим рассеяние электронов на точечном (бесструктурном) и бесспиновом ядре. Рассеяние на точечном объекте, естественно, всегда только упругое. Для дифференциального сечения рассеяния должна иметь место формула наподобие формулы Резерфорда. Однако эта формула должна отличаться от формулы Резерфорда в двух отношениях:

1. Она должна быть применима к релятивистским частицам (vc);

2. Она должна учитывать наличие ненулевого спина (1/2) у электрона.

Такая формула была получена Моттом в 1929 г. в рамках квантовой электродинамики и в пренебрежении отдачей ядра имеет вид

(1.5)

Множитель cos^2™/2 появляется из-за наличия спина у электрона. Формула Мотта получена в предположении бесструктурности (точечности) ядра. Если ядро - протяженный сферически симметричный и бесспиновый объект с плотностью заряда (r), то экспериментальное сечение упругого рассеяния электронов на н¸м будет отличаться от моттовского неким дополнительным множителем, который определяется только кулоновским взаимодействием и называется кулоновским форм-фактором

_ýêñï = |F|². (1.6)

Величина форм-фактора F зависит от (r) и может быть рассчитана для любого (r), т.к. известен характер взаимодействия электронов с любым заряженным объектом - это электромагнитное взаимодействие. Электроны не участвуют в ядерном (сильном) взаимодействии и взаимодействуют с ядром почти исключительно посредством электромагнитного поля. Это важное преимущество электронов по сравнению с другими зондирующими частицами, такими, например, как , p, n, которые участвуют в ядерных взаимодействиях.

Кроме того, на современном уровне знаний электрон можно считать точечной частицей. Вплоть до расстояний 10^-16 см (предел, достигнутый на сегодняшний день) у электрона не обнаружена структура (отличие от точечности). Таким образом, в форм-фактор упругого рассеяния дает вклад только (r) ядра. Схема нахождения (r) такова. Определяют _ýêñï и затем сравнивают с . Из их различий находят F. Подбирают такое (r), которое воспроизводит значение F:

_ýêñï F (r).

В свою очередь, т.к. заряд ядра создается протонами, (r)=Ze|_p()|², ãäå _p(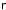) - волновая функция протона в ядре.

Вообще говоря, форм-фактор зависит от величины импульса q, которое получило ядро при рассеянии, - так называемого “переданного импульса”.

Можно показать, что упругий кулоновский форм-фактор следующим образом связан с (r)

F , (1.7)

ãäå - переданный ядру импульс=(₀-) (₀ è импульсы электрона до и после рассеяния). Формула (1.7) может быть получена в рамках классической оптики методом многолучевой интерференции. Множительучитывает сдвиг фаз между падающими электронными волнами де Бройля и упруго (когерентно) рассеянными, распределенными по всему объему ядра. Таким образом, учитываются волновые свойства рассеиваемых частиц, приводящие к интерференции от различных участков ядра.

Ðèñ.1.8 показывает (r) для нескольких ядер.

Простейшим приемлемым приближением для (r) считается двухпараметрическое распределение Ферми (рис. 1.9)

(r). (1.8)

Величину R, являющуюся радиусом полуплотности, будем в дальнейшем называть радиусом ядра. Радиус ядра описывается приближенной формулой

R = (1.2A^1/3-0.5) ôì. (1.9)

Для ядер с A>20 радиус R с точностью не хуже 20% можно получить из соотношения

R1.2A^1/3 ôì.

Параметр “a” связан с толщиной поверхностного слоя t соотно-шением t=(4ln3)a4.4a. Как показывает опыт, толщина поверх-ностного слоя одна и та же для всех ядер: t 2.4 фм (a 0.55 фм).

Ðèñ. 1.9

Наряду с упругим кулоновским рассеянием существует и упругое магнитное (для ядер с отличным от нуля спином), из которого можно извлечь распределение намагниченности (магнитного момента) внутри ядра. Существует и упругий магнитный форм-фактор. Вклады кулоновского и магнитного форм-факторов можно разделить.