6. Энергия симметрии. Роль принципа Паули.

Зависимость Z от A для стабильных ядер.

Чтобы получить правильный ход линии стабильности, необходимо учесть принцип Паули (ядро состоит из фермионов, подчиняющихся этому принципу). Вследствие этого ядра, у которых нуклонов одного типа больше, чем другого, имеют меньшую энергию связи, чем ядра с одинаковым числом протонов и нейтронов. Это хорошо видно из рис.2.5, где показано расположение 4-х нуклонов по уровням энергий в прямоугольной потенциальной яме в некоторой условной модели (наподобие модели Ферми-газа) для двух случаев:

à) 2 протона + 2 нейтрона (без учета кулоновской энергии);

á) 4 нейтрона.

Ðèñ.2.5

Предполагаем, что каждый уровень характеризуется лишь одним набором квантовых чисел и поэтому в соответствии с принципом Паули может быть занят лишь одним нуклоном каждого типа.

Считая, что уровни эквидистантны и расстояние между ними (а также глубина наиболее мелко сидящего уровня) равны E, получаем для левого варианта (а), энергию связи (т.е. энергию, необходимую для того, чтобы “достать” все нуклоны из потенциальной ямы) W_a = 14E, а для правого (б) - W_á = 10E, ò.å. W_a>W_á. Если даже создать ядро из одних нейтронов или протонов, то оно путем процессов np (или pn) перейдет в ядро с приблизительно равным числом нейтронов и протонов (эти процессы – не что иное как -распад (см. Лекцию 4)).

Член в формуле Вайцзеккера, который учитывает стремление ядра иметь в основном состоянии симметричное расположение по уровням нейтронов и протонов (симметрийный член), может быть записан в следующем виде:

E_ñèìì. (2.10)

Квадратная степень в числителе отражает тот факт, что энергия симметрии должна возрастать при росте относительного числа нуклонов любого типа. Появление множителя связано с реальным сближением ядерных уровней с ростом A. Слагаемое (2.10) должно быть добавлено в формулу Вайцзеккера со знаком “минус” потому, что отклонение от симметрии уменьшает энергию связи. Итак, с учетом уже имеющихся членов (2.7)-(2.10), для энергии связи ядра в модели жидкой капли получаем

W(A,Z) = a_vA - a_sA^2/3 - -, (2.11)

где хорошую подгонку под экспериментальные данные дает следующий набор констант:

a_v = 15.6 ÌýÂ

a_s = 17.2 ÌýÂ

a_c = 0.72 ÌýÂ

a_sym = 23.6 ÌýÂ.

Равновесное число протонов Z_ðàâí (линия стабильности) в ядре при фиксированном A определяется минимумом по Z суммы 3-его и 4-го членов в (2.11), откуда легко получить

Z_ðàâí . (2.12)

Видно, что Z_ðàâí < 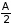. При отсутствии кулоновской энергии Z_ðàâí = . При учете кулоновской энергии линия стабильности с ростом Z вс¸ более смещается в сторону большего числа нейтронов.

7. Эффект спаривания.

Четно-четные, нечетные и нечетно-нечетные ядра.

С помощью формулы (2.11) можно описать энергию связи ядер (исключая легкие с A20) с точностью 1%. Однако имеются “пульсации” на уровне 1-2 МэВ, которые объясняются специфическим свойством NN-взаимодействия - в основном состоянии ядра возникает дополнительная связь между двумя нуклонами одного типа (двумя протонами или двумя нейтронами), занимающими один и тот же энергетический уровень. Этот эффект невелик ( 1-3 МэВ) т.е. всего 0.2% от энергии связи ядра, но четко виден в зависимости энергии связи от A, Z и N. Он демонстрируется на рис.2.6 для энергии отделения нейтрона изотопов Ce (церия).

Ðèñ. 2.6

Видно, что энергия отделения нейтрона возрастает на 2-3МэВ, когда их число становится четным. Это объясняется обсуждаемым особым свойством NN-взаимодействия: “возникновением в основном состоянии ядра дополнительной связи между двумя нуклонами одного типа, находящимися на одном и том же энергетическом уровне”. Качественно этот эффект иллюстрируется рис.2.7, где схематически показано, как меняется энергия отделения внешнего нейтрона при последовательном увеличении их числа.

Рис. 2.7. Спаривание нуклонов в ядре. Энергия спаривания 1-3 МэВ. В верхней части рисунка показаны проекции моментов у спариваемых нуклонов (подробнее в Лекции 7).

С точки зрения обсуждаемого эффекта (или, как говорят сил спаривания) все ядра разбиваются на три типа:

- четно-четные ядра (все нуклоны в основном состоянии спарены и положительная добавка к энергии связи наибольшая);

- нечетно-нечетные ядра (не спарены в основном состоянии по одному нуклону каждого типа и добавка к энергии связи наименьшая);

- промежуточный случай - нечетные ядра (один нуклон в основном состоянии неспарен).

Спаривательное слагаемое E_ñï в формуле для W(A,Z) условились записывать так, чтобы для нечетных ядер оно было равным нулю. В этом случае наилучшее воспроизведение экспериментальных данных дает следующая формула:

E_ñï = A^-3/4, (2.13)

ãäå =+ || - четно-четные ядра;

= 0 - нечетные ядра;

= - || - нечетно-нечетные ядра;

è || = 34 ÌýÂ.

Итак, окончательное выражение для энергии связи ядра (формула Вайцзеккера) имеет следующий вид:

W(A,Z) = a_vA - a_sA^2/3 - -+ A^-3/4 (2.14)

Вклад различных членов в формулу для удельной энергии связи иллюстрируется рис.2.8.

Ðèñ. 2.8

Приведем распределение числа стабильных ядер в зависимости от типа (четно-четные, нечетные, нечетно-нечетные).

Таблица 2.1

Z	N	A	число стабильных ядер
÷ (четное)	÷	÷	165
í (нечетное)	÷	í	53
÷ (четное)	í	í	57
í (нечетное)	í	÷	8
			всего: 283

Стабильные нечетно-нечетные ядра: ,,,.

Долгоживущие нечетно-нечетные ядра с измеренным процентным содержанием в естественной смеси изотопов: ,,,.

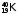В заключение приведем таблицу синтезированных сверхтяжелых элементов с Z100:

Таблица 2.2