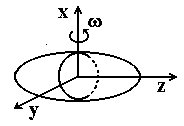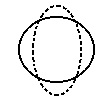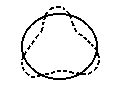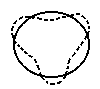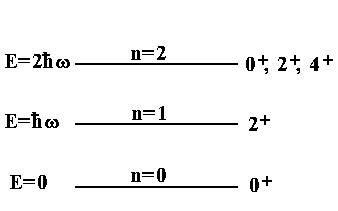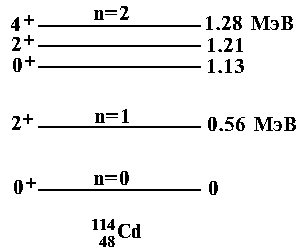5. Вращательные уровни ч¸тно-ч¸тных

несферических (деформированных) ядер.

Пусть имеется ядро в виде аксиально-симметричного вытянутого эллипсоида и, считая, что его ось симметрии совпадает с осью z, рассмотрим его вращение, например, вокруг оси x (следует напомнить, что вращение ядра вокруг оси симметрии и, как частный случай, вращение сферического ядра вокруг любой оси с точки зрения квантовой механики невозможно).

Классическая энергия вращения дается выражением

Ðèñ. 7.13

Eâð , (7.16)

где G - момент инерции эллипсоида, а L - орбитальный момент. В основном состоянии (ground state) четно-четного ядра (т.е. при отсутствии вращения) его спин J_gs=0. Если такое ядро вращается, то его спин целиком обусловлен этим вращением и J=L. Переходя к квантовой механике, т. е. производя замену J^{2 2}J(J+1), получаем

E_âð J(J+1). (7.17)

Очевидно, волновой функцией вращающегося ядра является собственная функция оператора , т.е. сферическая функция Y_JM. При этом J=0, 2, 4, ..., что следует из соображений симметрии. Бесспиновое ядро, имеющее форму аксиально симметричного эллипсоида, не меняется при пространственной инверсии (отражении в плоскости xy), т. е. переходит само в себя. Поэтому волновая функция такого ядра симметрична или ч¸тна, что исключает J=1, 3, 5,... . Таким образом, четность вращающихся состояний +1.

Примером вращательных уровней являются нижние уровни ядра (ðèñ.7.14)

Ðèñ. 7.14

Характерным признаком вра-щательных уровней (помимо последовательности их спинов-четностей Jp=0+, 2+, 4+, 6+, 8+, ... для четно-ч¸тных ядер) является пропорциональность энергии этих уровней величине J(J+1). Если в рассматриваемом примере выбрать G таким, чтобы энергия 1-го возбужденного уровня 2+ была равна 93 кэВ, то, ис-пользуя формулу (7.17), получим величины энергий уровней, приведенные на рисунке в скоб-

ках. Близость рассчитанных и опытных значений подтверждает вращательную природу уровней . По мере приближения к магическим (сферическим) ядрам G уменьшается и E_âð увеличивается. При этом вращательные уровни уходят вверх. Ещ¸ раз подчеркнем, что у сферических ядер вращательных состояний нет.

6. Колебательные (вибрационные) уровни ч¸тно-ч¸тных

сферических ядер

У таких ядер вращательные состояния отсутствуют или лежат очень высоко и низкоэнергичная часть спектра обусловлена колебаниями поверхности ядра вокруг равновесной формы. Возможные колебания поверхности ядра показаны на рис.7.15. Монопольные (J=0) колебания, в силу несжимаемости ядерной материи, лежат высоко. Низкоэнергичная часть колебательного спектра - квадрупольные (J=2) колебания, затем - октупольные (J=3) и т. д.

J=0	J=2	J=3
монопольные	квадрупольные	октупольные

Ðèñ. 7.15. Сплошной линией показана равновесная (сферическая) форма ядра, а пунктиром два крайних (различающихся половиной периода) состояния, которые принимает ядро в процессе колебаний.

Важно подчеркнуть, что в спектре поверхностных колебаний отсутствуют дипольные (J=1) колебания, поскольку в процессе малых колебаний этого типа ядро перемещается как единое целое без изменения своего внутреннего состояния (рис.7.16). При таких колебаниях меняется положение центра тяжести ядра. Внутреннего возбуждения ядра не происходит.

Ðèñ. 7.16

Если говорить об осцилляторе, способном совершать гармонические колебания какой-то одной мультипольности (только монопольные, только квадрупольные, только октупольные и т.д.), то, как известно из квантовой механики, уровни энергии такого осциллятора даются выражением

E_n = (n +5/2),

где n - целое число, включая нуль (число фононов), а - энергия одного фонона. Отсюда следует, что минимальная энергия поверхности ядра (энергия его основного состояния) E₀=5/2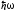, а энергия возбуждения малых гармонических колебаний одной мультипольности определяется соотношением

E_êîë = n. (7.18)

Таким образом, для фононов определенной мультипольности (например, квадрупольных) спектр эквидистантен - 1 фонон, 2 фонона, 3 фонона и т.д. Одному квадрупольному фонону ч¸тно-ч¸тного ядра отвечает возбуждение с J^p=2⁺. Состояние 2-х и более квадрупольных фононов такого ядра также имеют положительную четность. Таким состояниям отвечает момент J получающийся квантовомеханическим векторным сложением моментов отдельных квадрупольных фононов. При этом, однако, для двух квадрупольных фононов результирующие J=1 и 3 исключаются, т.к. такие значения J запрещены для двух тождественных фононов, подчиняющихся статистике Бозе-Эйнштейна. Поэтому из двух квадрупольных фононов в четно-четном ядре формируются лишь возбуждения с J^p=0⁺, 2⁺ è 4⁺, в идеальном случае вырожденные по энергии. Идеальный спектр нижних квадрупольных возбуждений ч¸тно-ч¸тного сферического ядра и реальный спектр сравниваются на рис.7.17.

Ðèñ. 7.17