- •1. Систематика частиц. Фундаментальные частицы.
- •2. Основные узлы фундаментальных взаимодействий.
- •3. Законы сохранения в мире частиц. Барионное и лептонное
- •Законы сохранения
- •4. Сильные взаимодействия. Адроны.
- •5. Кварки
- •Характеристики кварков
- •6. Кварковая структура легчайших барионов и мезонов
- •7. Кварковые атомы
7. Кварковые атомы
В
предыдущем разделе даны примеры того,
как выглядит кварковое строение легчайших
адронных супермультиплетов - одного
барионного и одного мезон/антимезонного.
Все остальное многочисленное семейство
адронов так же распадается на
супермультиплеты, формируемые сочетаниями
из трех или двух кварков - qqq (барионы),

 (антибарионы), q
(антибарионы), q (мезон/антимезо-ны). Таким образом, адроны
можно рассматривать как “кварковые
атомы” (или ядра). Сравним известные
образования (ядра) из трех нуклонов с
кварковой структурой самих нуклонов:
(мезон/антимезо-ны). Таким образом, адроны
можно рассматривать как “кварковые
атомы” (или ядра). Сравним известные
образования (ядра) из трех нуклонов с
кварковой структурой самих нуклонов:
 =
pnn;
=
pnn;  = ppn; (9.12)
= ppn; (9.12)
n = udd; p = uud.
Такое сравнение еще раз показывает, что с открытием кварков достигнут новый уровень структуры материи (новая ступень квантовой лестницы).
Кварки, образующие адроны, могут находиться в состояниях с различными орбитальными моментами. Спины этих кварков могут быть ориентированы различным образом. Поэтому для одной и той же кварковой комбинации допустимы различные значения полного момента и четности Jp. Энергия (масса) фиксированной кварковой комбинации зависят от Jp, т.е. для каждой кварковой комбинации получаем набор энергий (масс). Такова суть спектроскопии адронов, которая, по-существу, не отличается от атомной или ядерной спектроскопии. Единственное отличие, о котором здесь нужно сказать, состоит в том, что если у атома (или ядра) с определенным внутренним составом частиц меняется энергия и квантовые числа, то это означает переход в другое состояние этого же атома (ядра). В физике адронов изменение энергии (массы) и квантовых чисел фиксированной кварковой комбинации означает переход к другой частице (другому адрону со своим обозначением). Таким образом, в богатстве адронов скрыто все многообразие межкварковых возбуждений. Отмеченное отличие, однако, не принципиальное, а скорее терминологическое.
Рассмотрим вопрос о том, как ориентированы спины кврков в нуклонах, каковы их орбитальные моменты и почему у нуклонов Jp=1/2+. Возьмем, для примера, протон: p=uud. Протон - самое нижнее (основное) состояние кварковой комбинации uud. Как и в атомной (ядерной) спектроскопии основные (и самые нижние возбужденные) состояния отвечают нулевым орбитальным моментам составных частиц. Поэтому результирующий орбитальный момент L кварков в протоне равен нулю и полный момент протона получается сложением лишь спинов кварков. Оказывается, что в протоне у одного из кварков спин направлен противоположно двум другим, а именно, p=uud. В итоге получаем для протона J=1/2 и (т.к. внутренние четности кварков положительны) ч¸тность протона
P=uud (-1)L=0 = (+1)(+1)(+1)(-1)0=+1.
То же справедливо для всех других членов мультиплета легчайших барионов с Jp=1/2+ (ðèñ. 9.7).
У любой частицы, входящей в состав супермультиплета легчайших мезонов (рис. 9.8), орбитальный момент кварков также равен нулю. Спины кварка и антикварка антипараллельны () и суммарный момент мезона/антимезона этого нонета J=0. Т.к. внутренняя четность кварка +1, а антикварка -1. то четность мезона нонета
P=q (-1)L=0
= (+1)(-1)(-1)0=-1.
(-1)L=0
= (+1)(-1)(-1)0=-1.
В итоге для легчайших мезонов/антимезонов имеем Jp=0-.
С учетом всего вышеизложенного можно записать следующие формулы для определения четности мезонов/антимезонов, барионов и антибарионов:
P(мезон/антимезон)
= q
 = (+1)(-1)(-1)L
=
-(-1)L;
= (+1)(-1)(-1)L
=
-(-1)L;
P(барион)
= qqq = (+1)(+1)(+1)(-1)L
= (-1)L;
(9.13)
= (+1)(+1)(+1)(-1)L
= (-1)L;
(9.13)
P(антибарион)
=
 = (-1)(-1)(-1)(-1)L
= -(-1)L,
= (-1)(-1)(-1)(-1)L
= -(-1)L,
где L - результирующий орбитальный момент кварков в адроне.
8. Декуплет барионов с Jp=3/2+. Распады -резонансов.
Кварковая диаграмма нуклон-нуклонного взаимодействия.
В качестве последнего примера рассмотрим кварковую структуру еще одного супермультиплета барионов - декуплета с Jp=3/2+ (нижняя строчка выражения (9.10)). Этот декуплет показан на рис.9.9.

Ðèñ. 9.9
Верхнюю строчку фигуры образуют частицы со странностью S=0. Эти частицы - всевозможные тройные комбинации из двух легчайших кварков - u и d. Всего возможны 4 таких комбинации. Они отличаются проекцией изоспина I3 и образуют изоспиновый квартет (I=3/2). Следующий ряд (S=-1) - это все комбинации из двух нестранных (u и d) кварков и одного странного (s). Возможны три таких комбинации. Они образуют изоспиновый триплет (I=1). Ниже (S=-2) - это ряд частиц, в состав которых входит два s-кварка. Таких частиц две - dss и uss - и они образуют изодублет (I=1/2). Наконец, самая нижняя частица - это -, состоящая из трех s-кварков. Очевидно, что изоспин этой частицы равен 0 (изосинглет).
Сопоставление рис. 9.7 и 9.9 показывает, что по сравнению с октетом барионов Jp=1/2+ в декуплете Jp=3/2+ появились частицы, состоящие из одинаковых кварков - ddd, uuu, sss. Эти частицы, расположившись в углах, превратили “шестиугольник” октета в “треугольник” декуплета. Вопрос о том, почему этих трех комбинаций одинаковых кварков нет в октете Jp=1/2+, мы отложим до лекции 10, где будет дано (на качественном уровне) изложение квантовой хромодинамики (КХД).
Остальные (неугловые) кварковые комбинации - это повторение комбинаций октета Jp=1/2+. Так кварковые комбинации декуплета udd и uud аналогичны нейтрону и протону. Отличаются же они от нейтрона и протона тем, что у обсуждаемых кварковых комбинаций декуплета Jp=3/2+(à íå Jp=1/2+). То же можно сказать и о других общих кварковых комбинациях октета и декуплета. Экспериментальное исследование барионов декуплета показывает, что результирующий орбитальный момент кварков в нем L=0 и спины кварков параллельны (). Таким образом, полный момент частиц декуплета J=3/2. Четность P частиц декуплета находим, пользуясь правилом (9.13):
P(декуплет) = (-1)L=0 =+1. (9.14)
Итак, получаем для спина и четности декуплета Jp=3/2+.
Все общие (с октетом) кварковые комбинации декуплета есть возбужденные состояния (резонансы) соответствующих частиц октета. o-Резонанс - это возбуждение нейтрона, +-резонанс - это возбуждение протона и т.д. Звездочка (*) справа вверху в обозначении * и *-гиперонов декуплета отражает это обстоятельство. Отсутствие же в декуплете частицы аналогичной частице октета с I=0 также объясняется особенностями КХД (Лекция 10).
Возбуждения нуклонов, отвечающие o è +-резонансам, состоят в перевороте спина одного из кварков, после чего спины всех кварков направлены в одну сторону. То же можно сказать и о возбуждениях и -гиперонов, отвечающих частицам * и *. Переворот спина кварка в нуклоне, как видно из массы нуклона и -резонанса, требует энергии около 300 МэВ. Именно этот тип трехкваркового возбуждения наблюдал в 1951 г. Ферми при рассеянии пионов на протонах (Лекция 8).
Кроме -, все частицы декуплета - резонансы. Они распадаются за 10-23 сек на соответствующий барион октета и -мезон. Так -резонанс распадается на нуклон и пион: +нуклон. Например, ++-резонанс распадается единственным способом
++ + + p. (9.15)
Для распада o-резонанса существует две возможности
o o + n, (9.16)
o - + p.
и так далее.
Кварковая диаграмма распада (9.15) имеет вид
|
|
Ðèñ. 9.10 |
“Вилка”
 в правой части диаграммы возникла в
результате рождения пары
в правой части диаграммы возникла в
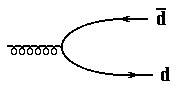
результате рождения пары глюоном (рис. 9.11).
глюоном (рис. 9.11).
|
|
Ðèñ. 9.11 |
Этот глюон был испущен одним из трех u-кварков ++-резонанса. Однако, как уже отмечалось выше, глюоны на диаграммах сильного взаимодействия обычно не рисуются (они лишь подразумеваются).
В заключение раздела изобразим на кварковом уровне диаграмму межнуклонного (ядерного) взаимодействия между нейтроном и протоном. Ранее (Лекция 5) мы изображали это взаимодействие как обмен -мезоном (рис. 9.12).
|
|
Ðèñ. 9.12 |
Кварковая диаграмма такого обмена показана на рис.9.13.
|
|
Ðèñ. 9.13 |
Мы видим, что ядерное взаимодействие - это некий остаток сильного (межкваркового) взаимодействия. Подобным образом межмолекулярные (или межатомные) силы - остаток более фундаментальных электромагнитных сил.