2. Основные узлы фундаментальных взаимодействий.

Кварковые диаграммы.

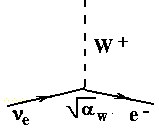
Элементарные узлы всех фундаментальных взаимодействий рисуют на уровне фундаментальных частиц, т.е. на кварк-лептонном уровне. На этом же уровне изображают все диаграммы процессов в мире частиц. Эти диаграммы являются комбинациями элементарных узлов. Типичные элементарные узлы взаимодействий показаны на рис. 9.1.

сильное
электромагнитное
слабое
гравитационное

Ðèñ. 9.1

На месте электрона в правом узле электромагнитного взаимодействия может быть любой заряженный лептон (антилептон). В случае слабого взаимодействия в качестве примера даны узлы трех конкретных процессов du+W^-, _ee^-+W⁺, _ee+Z. Узлы слабых взаимодействий других возможных процессов строятся аналогично.

Заменой на диаграмме всех частиц на античастицы можно получить диаграмму процесса с участием античастиц.

Распад нейтрона np+e^-+_e - это, по-существу, распад в н¸м d-кварка по той же схеме du+e^-+_e (d-кварк несколько тяжелее u-кварка). Диаграмма распада нейтрона на кварк-лептонном уровне выглядит так:

Ðèñ. 9.2

Диаграмма ^--мезона до распада имеет следующий вид

Ðèñ. 9.3

^--Мезон испытывает распад за счет слабого взаимодействия по схеме ^--+. На кварковом уровне этот процесс выглядит так: d+^-+и диаграмма такого распада имеет вид

Ðèñ. 9.4

Следует отметить, что на диаграммах обычно не указываются глюоны, т.к. обмен ими, в силу большой величины константы _s, происходит часто и различными способами. Другие калибровочные бозоны (, W, Z и гравитон) всегда указываются, т.к. обычно происходит однократный обмен этими частицами (следствие малости констант _e, _w è _G).

3. Законы сохранения в мире частиц. Барионное и лептонное

квантовое число. Странность. Частицы-античастицы.

В процессе взаимодействий и превращений частиц выполняется ряд законов сохранения. Они двух типов - аддитивные и мультипликативные (разъяснение - ниже в этом разделе). Ряд законов сохранения универсален, т.е. выполняется всегда (при всех взаимодействиях). Другие - в некоторых взаимодействиях не выполняются (нарушаются).

К универсальным законам сохранения относятся те, которые обусловлены инвариантностью уравнений движения относительно трансляций (сдвигов) в пространстве и во времени. С этими типами симметрий - однородностью пространства и времени - связано существование законов сохранения импульса и энергии изолированных систем частиц. Изотропность 3-мерного пространства, т.е. инвариантность уравнений движения относитель-но поворотов (вращений), приводит к закону сохранения момента количества движения.

Если преобразование волновой функции, отвечающее закону сохранения, имеет непрерывный характер (т.е. может быть как угодно малым), то соответствующий закон сохранения аддитивен, т.е. в реакции

a + b c + d + ... (9.1)

сохраняется сумма соответствующих характеристик (или квантовых чисел):

N_a + N_b = N_c + N_d + ... = const. (9.2)

Трансляции и повороты - непрерывные преобразования и соответствующие законы сохранения (энергии, импульса и момента количества движения) - аддитивны. Аддитивными сохраняющимися величинами являются также электрический заряд Q, барионное квантовое число (или барионный заряд) B, лептонное квантовое число (или лептонный заряд) L, изоспин I, а также ряд других квантовых чисел, имеющих кварковую природу - Странность (strangeness) S, Очарование (charm) C, Bottom (èëè Beauty - красота) B, Top (èëè Truth - истина) T.

С какими типами симметрий связаны законы сохранения всех этих аддитивных квантовых чисел (Q, B, L, I, S, C, B è T)? В настоящее время известен ответ лишь для электрического заряда Q и изоспина I. Так, сохранение изоспина в сильных взаимодействиях - следствие инвариантности этого взаимодействия относительно поворотов в специальном изоспиновом (зарядовом) пространстве (Лекция 5). Сохранение же электрического заряда есть отражение так называемой локальной калибровочной симметрии электро-магнитного взаимодействия. Суть этой симметрии в следующем. Пусть - волновая функция частицы с зарядомq, удовлетворя-ющая уравнению Шредингера. Преобразуем эту функцию в функцию (x) с помощью следующей операции

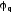(x) = (x), (9.3)

которая меняет фазу волновой функции заряженной частицы различным образом в разных точках пространства (такие преобразования называют локальными калибровочными). Можно показать (последнее не входит в задачу курса), что это не меняет наблюдаемой физической картины при условии, если заряды взаимодействуют посредством дальнодействующего (электро-магнитного) поля, описываемого системой уравнений Максвелла, причем переносчик такого взаимодействия должен быть безмассовым (фотон), а электрический заряд должен сохраняться.

Барионное квантовое число (или барионный заряд) B имеют лишь барионы - адроны с полуцелым спином. Для них B=+1, для антибарионов B=-1. Барионный заряд сохраняется в сильных, электромагнитных и слабых взаимодействиях.

Лептонное квантовое число L (лептонный заряд) присущ только лептонам. Существует три типа лептонного заряда L_e, L è L, каждый из которых сохраняется в отдельности. Лептонным зарядом L_e=+1 обладают лептоны 1-го поколения (_e, e^-), L=+1 для лептонов 2-го поколения (, ^-) è L=+1 для лептонов 3-го по-коления (, ^-). У антилептонов знак соответствующего лептонного заряда -1 (L_e=-1 äëÿ _e è e⁺; L=-1 äëÿ è⁺; L=-1 äëÿ è⁺).

Протон - самый легкий барион и если закон сохранения барионного заряд абсолютен, то протон должен быть стабильной частицей. Экспериментальные данные свидетельствуют о том, что время жизни протона _p>10³² лет. В теориях Великого Объединения (единых теориях сильного, электромагнитного и слабого взаимодействий) предсказывается нестабильность протона. Но предсказываемые времена распада неопределенны и могут существенно превышать величину 10³² лет. Поиски распада протона ведутся. Однако при _p10³⁵ лет такой распад практически невозможно обнаружить. В предсказываемых распадах протона нарушается и закон сохранения лептонного заряда. Мы, однако, будем относиться к законам сохранения барионного и лептонного заряда как к универсальным, поскольку они выполняются во всех наблюдаемых процессах.

Если преобразование волновой функции дискретно, то соответствующий закон сохранения мультипликативен, т.е. в реакции (9.1) сохраняется произведение соответствующих характеристик (квантовых чисел)

N_aN_b = N_cN_d = const. (9.4)

Пример дискретных преобразований - операция зеркального отражения (пространственной инверсии). Инвариантность к такому преобразованию приводит к квантовому числу - четности P (о н¸м уже говорилось в Лекции 3). Все взаимодействия, кроме слабого, инвариантны к пространственной инверсии и для них справедлив закон сохранения P-четности в мультипликативной форме. О двух других дискретных преобразованиях - зарядовом сопряжении и обращении времени - и связанных с ними законах сохранения будет сказано в Лекции 13. Вплоть до этой лекции мы о них упоминать не будем.

Приведем перечень законов сохранения, действующих в мире частиц, с указанием их статуса. Эти законы можно разделить на два класса - универсальные (действующие во всех взаимодействиях) и те, которые в некоторых взаимодействиях не выполняются.

Первые 6 законов - универсальны, т.е. выполняются всегда (во всех взаимодействиях). Изоспин сохраняется только в сильных взаимодействиях. Остальные законы сохранения не выполняются в слабых взаимодействиях.

Мы видим, что в мире частиц действует много новых законов сохранения (с 9-го по 12-й). Эти четыре закона, а также, как мы увидим ниже, закон сохранения изоспина, напрямую связаны с кварковой структурой адронов, т.е. со специфическими квантовыми числами, присущими кваркам. Так квантовое число “странность” было введено в 1953 г. Гелл-Манном задолго до появления кварковой модели.

Таблица 9.3