
5. Дополнительные выводы о -распаде. Разрешенные и запрещенные
-Переходы. Переходы Ферми и Гамова-Теллера.
Для -переходов мы получили, что с ростом L (или J) поглощенного (излученного) фотона вероятность процесса резко падает, если >>R. Это же мы имеем и при -распаде. В этом случае вместо электромагнитных волн надо говорить о плоских монохроматических лептонных волнах, испускаемых ядром. Пространственная часть волновой функции лептонного излучения в этом случае имеет вид
 .
.
В системе центра инерции (сци) может быть записана в виде
(ñöè) =
 ,
,
ãäå
 - относительный волновой вектор (
- относительный волновой вектор ( - относительный импульс), а
- относительный импульс), а
 - относительная координата (радиус-вектор).
Далее (сци)=
- относительная координата (радиус-вектор).
Далее (сци)= разлагаем в ряд по состояниям с различными
относительными орбитальными моментами
L (формула (4.22)).
разлагаем в ряд по состояниям с различными
относительными орбитальными моментами
L (формула (4.22)).
Вводя затем условие >>R (kR<<1), и, повторяя рассуждения, использованные при рассмотрении электромагнитных переходов, приходим буквально к тем же выводам о резком снижении вероятности -переходов с ростом относительного орбитального момента L лептонной пары. Действительно характерные энергии -распада (1-2 МэВ) таковы, что, полагая R 5 фм, имеем
 0.02
- 0.05 << 1.
0.02
- 0.05 << 1.
Поэтому справедливо длинноволновое приближение и все сопутствующие ему выводы. В данном случае увеличение орбитального момента L на единицу приводит к уменьшению вероятности -перехода в 1/(0.02-0.05)2 102-104 раз. Максимальную вероятность (если они допустимы) имеют -распады с относительным моментом лептонной пары L=0. Они называются разрешенными. Остальные (L0) называют запрещенными, причем степень запрета равна L. Есть разрешенные переходы двух типов (т.к. se=s=1/2)
Ферми ( ),
),
Гамова-Теллера ( ).
(4.26)
).
(4.26)
Итак, мы получили, что во всех рассмотренных видах радиоактивного распада ядер (, , ) вероятность распада зависит от относительного орбитального момента L продуктов распада. Во всех случаях (при прочих равных условиях) вероятность падает с ростом L. Однако в -распаде это не является определяющим фактором формирования вероятности распада. Значительно более важную роль там играет кулоновский барьер. В - и -распадах, где кулоновский барьер не играет роли, фактор подавления вероятности за счет орбитального момента становится определяющим.
Пример. Покажем, что соотношение неопределенностей запрещает электрону при -распаде долго оставаться внутри ядра.
Характерные
энергии -распада таковы, что
 <<1,
где p - относительный импульс лептонной
пары при -распаде, а R - радиус ядра.
Таким образом, имеем неравенство
<<1,
где p - относительный импульс лептонной
пары при -распаде, а R - радиус ядра.
Таким образом, имеем неравенство
 .
В то же время, поскольку неопределенность
в импульсе электрона pep
и неопределенность в его координате
xeR,
то из этого неравенства следует
.
В то же время, поскольку неопределенность
в импульсе электрона pep
и неопределенность в его координате
xeR,
то из этого неравенства следует
 ,
что противоречит соотношению
неопределенностей
,
что противоречит соотношению
неопределенностей
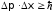 .
Таким образом, электрон -распада не
может долго оставаться в ядре, не нарушая
соотношение неопределенностей.
.
Таким образом, электрон -распада не
может долго оставаться в ядре, не нарушая
соотношение неопределенностей.
