Промежуточные бозоны.

-Распад это самопроизвольное испускание лептонов (e,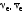). За этот процесс ответственно слабое взаимодействие. -Активные ядра разбросаны по всей системе элементов (рис.2.1). Есть три вида -распада. Происходящие при этом внутри ядра превращения нуклонов и энергетические условия соответствующего вида -распада выглядят так:

1. ^- (np+e^-+), M(A,Z) > M(A,Z+1) + m_e,

2. ⁺ (pn+e⁺+), M(A,Z) > M(A,Z-1) + m_e, (4.15)

3. e-захват (p+e^-n+), M(A,Z) + m_e > M(A,Z-1).

Времена -распада лежат в интервале t_1/2()=0.1 ñåê - 10¹⁷ лет. -Распад, за который ответственны ядерные силы, может происходить за времена существенно более короткие (до 310^-7 сек). На малую интенсивность слабых взаимодействий указывает и большое время жизни нейтрона (15 мин). -Распад со сравнимой энергией выделения (0.78 МэВ) идет в среднем за 10^-12 ñåê.

Энергия -распада

= [M(A,Z) - M(A,Z1) - m_e]c², (4.16)

Q_e = [M(A,Z) - M(A,Z-1) + m_e]c².

Она заключена в интервале от 18.61 кэВ () äî 13.4 ÌýÂ ().

Кулоновский барьер при -распаде можно не обсуждать. Он есть лишь для позитронов, образовавшихся внутри ядра. Главное то, что соотношение неопределенностей запрещает e долго оставаться внутри ядра (см. конец лекции).

При -распаде возникает три продукта с произвольным распределением по энергии. При этом энергетический спектр каждого продукта непрерывен (рис.4.5). При e-захвате - два продукта и спектр дискретен. Непрерывность -спектров (e) натолкнула Паули в 1930 г. на идею о существовании неизвестной нейтральной частицы с полуцелым спином и очень малой массой. Ферми назвал е¸ “нейтрино” (нейтрончик) после открытия в 1932 г. нейтрона.

Ðèñ. 4.5. Энергетические спектры лептонов при распаде

.

Нейтрино очень слабо взаимодействует с веществом и ускользает от наблюдателя. Е¸ пробег в твердой среде 10¹⁵ км. Лишь в 1956 г. Райнесу и Коуэну удалось экспериментально подтвердить существование нейтрино и оценить сечение его взаимодействия с веществом ( 10^-43 ñì²).

В настоящее время установлено, что слабое взаимодействие осуществляется переносом (обменом) так называемых промежуточных бозонов - частиц большой массы, которые являются квантами слабого поля, как фотоны - квантами электромагнитного поля. Масса этих бозонов 80(W) и 91(Z) ГэВ. Они открыты в 1983 г. в CERN (Европейская организация ядерных исследований, Швейцария). Исходя из массы промежуточных бозонов, можно оценить радиус действия слабых сил.

Появление W с m_wc² означает нарушение закона сохранения энергии на величину E=m_wc². Такие нарушения допустимы (ненаблюдаемы) в пределах временного интервала

,

(что следует из соотношения неопределенностей ). При этом виртуальная частица не может уйти на расстояние a_w большее, чем

210^-3 ôì.

В 1957 г. было установлено несохранение четности в слабых взаимодействиях.

Полезное соотношение между массой переносчика взаимодействия и радиусом соответствующих сил

. (4.17)

4. -Распад. Классификация фотонов. Правила отбора

для электромагнитных переходов. Вероятности электро-

магнитных переходов в длинноволновом приближении.

Ðèñ.4.6

С точностью до незначительной энергии отдачи ядра энергия -перехода равна разности энергий уровней. Ядерные состояния имеют определенные значения спина (J) и четности (P). Поэтому -переходы между ними также имеют определенные J(P).

Изучая -спектры, получают информацию о ядерных уровнях. Законы сохранения требуют, чтобы

_f = _i + èëè |J_i - J_f| J J_i + J_f

P_f = P_i P èëè P = P_i P_f. (4.18)

Рассмотрим классификацию фотонов по моменту и четности. Полный момент количества движения фотона J принимает целочисленные значения, начиная с единицы: J=1 (дипольный), 2 (квадрупольный), 3 (октупольный), ... . Спин фотона равен 1, т.е.

S = (J)_min = 1 - спин фотона.

Полный момент фотона равен векторной сумме его спина и орбитального момента : =+ (L - ранг входящих в волновую функцию фотона сферических функций Y_Lm). Далее опускаем индекс у полного момента фотона. Для фиксированного J фотона L=J1, J. Внутренняя четность фотона отрицательна (как квантов векторного поля). Поэтому полная четность фотона есть произведение его внутренней четности (-1) и орбитальной четности (-1)^L

P = (-1)^L = (-1)^L+1. (4.19)

Для фотонов с определенным J имеем разные L и, следовательно, разные четности (опускаем индекс у четности фотона)

L=J è P = (-1)^J+1 - магнитные (MJ) фотоны;

L=J1 è P = (-1)^J - электрические (EJ) фотоны.

Названия “магнитный” и “электрический” происходят от типа систем зарядов и токов, излучающих соответствующие фотоны. Колеблющийся электрический диполь (с изменяющимся электрическим дипольным моментом) излучает E1-фотоны, колеблющийся магнитный диполь - M1-фотоны и т.д.

Правила отбора по четности имеют вид:

P_iP_f = (-1)^J для EJ-фотонов;

P_iP_f = (-1)^J+1 для MJ-фотонов. (4.20)

Так как J1, переходы 00 с испусканием или поглощением одного фотона запрещены. Примеры простейших -переходов (рис.4.7):

Ðèñ. 4.7

Вероятность поглощения (испускания) фотонов может быть рассчитана в рамках квантовомеханической теории возмущений. При этом вероятности поглощения и испускания фотонов определенного типа и мультипольности будут одинаковы. В общем случае при переходе между двумя уровнями с J0 возможно поглощение (испускание) фотонов разного типа и мультипольности. Оценим вероятность поглощения фотонов в случае, когда >>R (длинноволновое приближение), прибегая лишь к самым простым рассуждениям.

Пусть на ядро падает плоская монохроматическая электромагнитная волна. Векторный потенциал для не¸ может быть записан в виде

, (4.21)

ãäå , - единичный вектор поляризации, ( - единичный вектор в направлении движения волны). При =E_f -E_i возможно поглощение этой волны ядром. можно придать смысл волновой функции фотона.

Плоская волна (4.21) не обладает определенным моментом J и четностью P. Но е¸ можно разложить на состояния с определенным L (и четностью), т.е. по функциям Y_Lm(,), набор которых является полным. Разложение выполним для зависящей от координат части , ò.å. äëÿ

Ðèñ. 4.8

, (4.22)

где - угол между è , Y_L0() не зависит от , а a_L(kr) - коэффициенты разложения (которые, как будет видно ниже, зависят от kr).

Квадраты коэффициентов a_L(kr) определяют вероятность обнаружить в плоской волне состояния с данным L (=1), ò.å. |a_L(kr)|² указывают вес (долю) участия в плоской волне фотонов с данным L.

Вероятность поглощения фотонов определенного типа (с определенным L) при прочих равных условиях пропорциональна вероятности обнаружить их в объеме ядра, т.е. величине |a_L(kr)|² в области 0 r R, где находится ядро (его считаем расположенным в начале координат).

Можно показать, что

,

где i - мнимая единица, а j_L(kr) - сферическая функция Бесселя первого рода порядка L.

Оценим величины j_L(kr), определяющие поведение a_L(kr), в длинноволновом приближении, т.е. при >>R. Условие это эквивалентно условию kR<<1 (). Итак, необходимо знать поведение j_L(kr) при 0 r R при дополнительном условии kr<<1. Асимптотическое выражение для j_L(kr) при kr0 следующее

. (4.23)

Далее для оценок полагаем r=R. С учетом того, что в выражения для вероятностей входят |j_L(kR)|², окончательно получаем

w(MJ) (kR)^2J ,

w(EJ) (kR)^2(J-1) 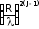(4.24)

Соотношения (4.24) можно записать в виде

(kR)² << 1,

(kR)² << 1. (4.25)

Переходы с E<10 МэВ отвечают условию >>R. Действительно, для фотона с энергией 10 МэВ

ôì = 120 ôì.

Даже для ядер с A200, у которых R 1.2A^1/3 фм 7 фм, имеем >>R.