5. Первые этапы объединения взаимодействий

В электрослабой модели (ЭСМ) объединены электромагнитные и слабые взаимодействия. Их константы сильно различаются (табл.8.2), однако имеют тенденцию к сближению при росте энергии. Дело обстоит примерно также, как и при объединении электрических и магнитных сил Максвеллом более века назад. Сила, действующая на заряженную частицу (сила Лоренца) имеет следующий вид

. (13.22)

При малых скоростях частицы (v<<c) магнитная сила много меньше электрической. При vc они одного порядка. То же можно сказать и об электрослабом объединении. Электромагнитные и слабые силы объединяются при энергиях 100 ГэВ.

Перечислим пройденные этапы объединения взаимодействий

- объединение электрических и магнитных сил (Максвелл, 1864 г.);

- объединение электромагнитных и слабых сил (Вайнберг, Салам, Глэшоу, 1967 г.).

6. Константы взаимодействий. Пропагатор.

Переопределение константы слабого взаимодействия.

Интенсивность (вероятность) различных взаимодействий характеризуется безразмерными константами . При энергиях 100 МэВ эти константы таковы

_s=1, _e10^-2, _w10^-6, _G10^-38.

Здесь _w обозначена константа слабого взаимодействия, использовавшаяся раньше в этом курсе без черты сверху (табл. 8.2).

В случае безмассовых переносчиков взаимодействий (глюон, фотон, гравитон) константы _i связаны с соответствующими зарядами g_i соотношением

, (i = s, e, G), (13.23)

причем g_ee.

В случае массивных переносчиков (W, Z) на вероятность взаимодействия существенно влияет и масса переносчика. Чем больше его масса, тем в узле сильнее нарушается закон сохранения энергии, тем “более виртуальным” становится переносчик взаимодействия и тем менее вероятен процесс. Введенное ранее значение константы слабого взаимодействия _w учитывало влияние на вероятность слабого процесса как собственно величины слабого заряда g_w, так и массы переносчиков m_w è m_z (далее везде будем писать только m_w). Поскольку в дальнейшем нас будут интересовать процессы при сверхвысоких энергиях, когда массой переносчиков можно пренебречь (полагая m_w0), то естественно сравнивать константы _i=g_i²/c, не учитывая массы переносчиков. В этой связи необходимо переопределить константу слабого взаимодействия в соответствии с формулой_w=g_w²/c. Именно для этой константы мы в дальнейшем и будем использовать обозначение_w, т.е. без черты сверху.

Переопределение константы слабого взаимодействия можно сделать, используя вид пропагатора, - функции, описывающей внутреннюю линию диаграммы Фейнмана. Пропагатор переносчика имеет вид (без доказательства)

пропагатор = , (13.24)

ãäå - квадрат четырех-импульса виртуальной частицы (). Пропагатор входит множителем в амплитуду A_i двухузловой диаграммы, как и константа взаимодействия _i, и с учетом этого амплитуда может быть записана в следующем виде

A_i 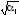пропагатор=_i = _i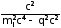, (13.25)

ãäå _i=g_i²/c и, как и везде в этом курсе, значок означает “пропорционально”.

Если бы переносчик взаимодействия был бы реальной частицей, то для него выполнялось бы релятивистское соотношение , и знаменатель в пропагаторе (13.24) обращался бы в нуль. Однако переносчик - частица виртуальная и для не¸ упомянутое релятивистское соотношение не выполняется (). Из (13.25) видно, что чем сильнее нарушается это релятивистское соотношение (т.е. чем “виртуальнее” частица-переносчик), тем ниже вероятность процесса.

Ðèñ. 13.3

Когда квадрат 4-импульса, переносимого W-бозоном, q² мал по сравнению с , пропагатор W-бозона перестает зависеть от переносимого им импульса

.

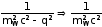Поэтому влияние массы промежуточного бозона (W и Z) на вероятность слабых процессов особенно велико при энергиях меньше 100 ÃýÂ.

Рассмотрим для определенности ситуацию при q²c² (1 ÃýÂ)² (m_pc²)², ãäå m_p - масса протона. Т.к. m_w>>m_p, то для амплитуды двухузловой диаграммы слабого процесса (рис.13.3) имеем согласно (13.25)

. (13.26)

Для двухузловой диаграммы электромагнитного процесса (масса переносчика нулевая) при том же квадрате переданного импульса

A_e . (13.27)

Из сравнения (13.26) и (13.27) видно, что при рассматриваемых энергиях (1 ГэВ) за счет массы промежуточного бозона константа слабого взаимодействия эффективно уменьшается на множитель порядка по сравнению с константой электромагнитного взаимодействия, осуществляемого обменом безмассовым фотоном. Именно это уменьшенное за счет массы переносчика значение использовалось ранее в этом курсе в качестве константы слабого взаимодействия_w

. (13.28)

Отсюда следует, что “освобожденная от влияния массы переносчика” константа слабого взаимодействия может быть оценена при низких энергиях как

_w 10^-6 10⁴ = 10^-2. (13.29)

Более точное значение этой константы при энергии 1 ГэВ следующее: _w=. Таким образом,_w>_e, т.е. “слабость” слабого взаимодействия по сравнению с электромагнитным - следствие большой массы промежуточных бозонов. Сам слабый заряд g_w даже больше электромагнитного (g_ee) примерно в 2 раза.