Гиромагнитные факторы электрона и нуклонов

частица	gl	gs
электрон	1	2
протон	1	5.58
нейтрон	0	-3.83

Ðèñ.3.4 Орбитальный и спиновый магнитный момент частицы

Значения 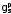è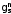определены экспериментально (впервые это было сделано Штерном в 1933 г.). Отличиеот 2 и неравенство нулюговорит о сложной структуре (неточечности) нуклона, который, как известно, состоит из кварков.

Вводят также понятие гиромагнитного фактора для каждого ядра

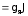. (3.32)

Колинеарность è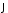очевидна, т.к. при вращении заряда магнитный момент должен совпадать или быть противоположным по направлению с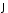. Ценность изучениясвязана с возможностью получения информации о спинах ядер.

7. Квантовомеханические моменты ядер

Наблюдаемые (квантовомеханические) электромагнитные моменты ядер всегда меньше их внутренних (классических) значений. Это связано с квантовомеханическими свойствами вектора спина ядра , который нельзя заставить ориентироваться точно вдоль фиксированного направления в пространстве (осиz). Этим направлением является, например, направление внешнего поля, используемого для нахождения величин статических моментов. Будем, для определенности, говорить об электрическом квадрупольном моменте ядра в форме вытянутого аксиально симметричного эллипсоида. Вектор спина 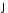образует с осьюz óãîë _M, определяемый соотношением (рис.3.5):

Ðèñ. 3.5

cos M = , ãäå M = J, (J-1), (J-2),..., 1/2(èëè 0).

В этой связи внешний наблюдатель воспринимает ядро при определенном M не как вытянутый аксиально-симметричный эллипсоид, а как объект, полученный усреднением всех возможных ориентаций этого эллипсоида относительно оси z (при неизменном угле _M). При этом конец вектора 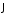с равной вероятностью оказывается в любой точке окружности, показанной на рисунке пунктиром. Очевидно, максимальное наблюдаемое значение квадрупольного моментаQ отвечает случаю, когда проекция íà îñüz максимальна, т.е. когда

cos _M=J = .

Именно это значение Q_M=J и принимают за наблюдаемое (квантовомеханическое) значение электрического квадрупольного момента ядра:

Q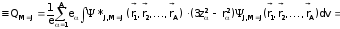

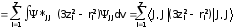, (3.33)

где суммирование по i относится к протонам.

Отличный от нуля квадрупольный момент Q можно обнаружить, помещая ядро в неоднородное электрическое поле E, в котором у ядра возникает дополнительная энергия взаимодействия, пропорциональная 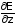Q. Таким полем, например, является электрическое поле электронной оболочки атома, в спектре которого в этом случае появляются добавочные линии сверхтонкой структуры.

Можно показать, что между наблюдаемым и внутренним квадрупольными моментами имеет место соотношение

Q = Q₀, (3.34)

откуда получаем, что Q=0 ïðè J=0 и 1/2. Это не означает, что ядро с такими спинами обязательно сферическое. Просто невозможно, изучая взаимодействие такого ядра с внешним неоднородным электрическим полем, “почувствовать” его несферичность, т.к. энергия квадрупольного взаимодействия равна нулю. Для ядра с J=0 это достаточно очевидно, т.к. у такого ядра нет выделенных направлений относительно осиz. Все направления равновероятны.

Наблюдаемый магнитный дипольный момент ядра определяется (аналогично электрическому квадрупольному) как его среднее значение в состоянии с максимальной проекцией спина на ось z (M=J):

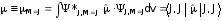, (3.35)

ãäå - оператор магнитного дипольного момента

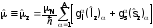. (3.36)

Очевидно средние значения операторов _x è _y , равны нулю.

Величину магнитного момента можно найти, определяя энергию его взаимодействия с внешним магнитным полем

E = -.

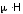В атоме взаимодействие магнитного момента ядра с магнитным полем электронной оболочки приводит к сверхтонкому расщеплению оптического спектра атома. Это дает возможность определить величину магнитного момента ядра (по величине расщепления), а также спин ядра (по количеству линий расщепления).

Наблюдаемые значения квадрупольных моментов ядер показаны на рис.3.3. Обращает на себя внимание следующее:

1. Их равенство нулю для магических ядер (Z, N =2, 8, 20, 50, 82, 126). Магические ядра - сферические. Вообще же сферических ядер мало.

2. Они растут при отходе от магических ядер, достигая наибольших значений в середине между магическими областями.

3. Большие величины квадрупольных моментов характерны для вытянутых ядер (Q>0). Вытянутых ядер больше, чем сплюснутых.

Можно показать прямым вычислением, что внутренний квадрупольный момент однородно заряженного эллипсоида дается выражением

Q₀ = Z(b² - a²), (3.37)

ãäå b è a полуоси (рис.3.5).

Если для оценки степени отклонения формы ядра от сферической ввести параметр деформации и средний радиус 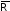, определяемые соотношениями

,

,

то можно записать

Q₀ = Z(b² - a²) = ². (3.38)

Обычно для ядер <0.6.

Пример. Докажем, что из определенной четности волновой функции системы частиц (например, ядра) следует равенство нулю е¸ электрического дипольного момента:

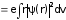. (3.39)

Здесь использовано то, что . При определенной четностифункциявсегда четна и подынтегральная функция в (3.39) нечетна, что и приводит к равенству нулю интеграла, а значит и электрического дипольного момента.

Более строгое выражение для электрического дипольного момента ядра

, (3.40)

где суммирование по i относится к протонам. Это более корректное выражение для не меняет сути доказательства.