5. Тождественность частиц.

Статистика. Фермионы и бозоны.

В микромире частицы одного типа неразличимы, т.е. имеет место принцип тождественности частиц. Перестановка двух одинаковых частиц не меняет состояние системы. Принцип тождественности можно сформулировать и так: гамильтониан системы частиц инвариантен относительно перестановки всех координат двух любых частиц одного типа. Поэтому должна быть новая квантовая характеристика (квантовое число) или сохраняющаяся физическая величина, отвечающая этому преобразованию.

Оператор перестановки ₁₂ и его собственные значения определяются следующим образом:

₁₂(1, 2,..., A) = (2, 1, ..., A) = (1, 2,..., A),

(1, 2,..., A) = ²(1, 2,..., A) = ( 1, 2,..., A).

Поэтому ²=1 è =1.

Ïðè =+1 ₁₂(1, 2,..., A) = (1, 2,..., A),

è (2, 1, ..., A) = (1, 2,..., A).

Частицы, входящие в состав таких систем, называются бозонами.

Ïðè =-1 ₁₂(1, 2,..., A) = -(1, 2,..., A),

è (2, 1, ..., A) = -(1, 2,..., A).

Частицы, входящие в состав таких систем, - фермионы.

Примеры: бозонов - , , ; фермионов - p, n, e.

У фермионов в одном состоянии - не более одной частицы (принцип Паули), у бозонов - сколько угодно. В квантовой теории поля показывается, что фермионы имеют полуцелый спин, а бозоны - целый. Лазер существует, т.к. фотоны являются бозонами.

Доказательство принципа Паули:

(2, 1, ..., A) = - (1, 2,..., A).

Пусть частицы 1 и 2 находятся в одинаковом состоянии. Тогда (1,2,...,A) и (2, 1, ..., A) суть одна и та же функция и =-, 2=0, =0, т.е. такого состояния нет.

6. Классические статические электромагнитные моменты ядер

Ядро, как система зарядов и токов, обладает статическими электрическими и магнитными мультипольными моментами. Обычно ограничиваются наблюдаемыми моментами нижайшей (не равной нулю) мультипольности в основном состоянии - электрическим квадрупольным и магнитным дипольным, которые дают ценные сведения о свойствах ядра. Электрический дипольный момент ядра равен нулю, что легко доказывается на основе закона сохранения четности (см. ниже).

Электрические моменты. Åñëè () - плотность распределения электрического заряда в системе, то из классической электродинамики известно, что

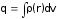
есть электрический монополь, т.е. полный (скалярный) заряд системы.

(i=1 (îñü x), 2 (y), 3 (z)) (3.23)

есть i-я компонента вектора электрического дипольного момента

.

(3.24)

есть одна из пяти линейно-независимых компонент тензора электрического квадрупольного момента. Электрический квадрупольный момент определяет взаимодействие ядра с градиентом внешнего электрического поля (например, создаваемого электронной оболочкой). При наличии электрического дипольного момента возникает его взаимодействие с напряженностью внешнего электрического поля. При отличии от нуля электрического заряда системы возникает его взаимодействие с внешним электрическим потенциалом.

Величины электрического дипольного и квадрупольного моментов зависят от выбора системы координат. В дальнейшем мы будем использовать так называемую внутреннюю систему координат, когда е¸ начало совпадает с центром распределения заряда и массы. Можно легко показать, что электрический дипольный момент обращается в нуль при совпадении центра заряда с центром массы системы. Равенство нулю ядерного электрического дипольного момента как раз и говорит о таком совпадении.

Будем под электрическим квадрупольным моментом понимать величину

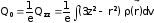. (3.25)

Если у ядра есть ось симметрии (как, например, у тела вращения), то значение Q₀ зависит от ориентации оси z внутренней системы координат относительно этой оси симметрии. |Q₀| - максимален, если ось z совпадает с осью симметрии и как раз эту величину и рассматривают как внутренний èëè классический квадрупольный момент ядра.

Q₀ характеризует отличие распределения заряда ядра от сферически симметричного (Q₀=0 для сферически симметричного ядра), т.е. характеризует форму ÿäðà (ðèñ.3.2).

Ðèñ. 3.2

Следует подчеркнуть, что ядерный спин направлен всегда вдоль оси симметрии. Это легко понять, пользуясь простой аналогией

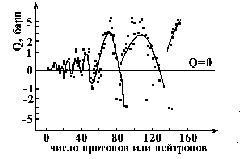
Ðèñ. 3.3

с классической механикой и рассматривая 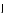как результат вращения ядра как целого вокруг оси. В этом случае ось вращения, совпадающая с вектором спина, и будет осью симметрии.

Ïðè Q₀>0 ядро - вытянутый вдоль оси z эллипсоид. При Q₀<0, ядро является сплюснутым (вдоль z) эллипсоидом (рис.3.2). Данные о ядерных квадрупольных моментах даны на рис.3.3. Квадрупольный момент измеряется в барнах (1б=10^-24 ñì²).

Магнитный дипольный момент. Классическое определение магнитного дипольного момента частицы с массой m и зарядом q

. (3.26)

В микромире аналогом классического момента является магнитный момент орбитального движения

, (3.27)

ãäå 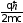- магнетон.

Если выражать в магнетонах, аâ, òî

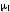[магнетон] = . (3.28)

Обобщая (3.27) на случай магнитного момента, возникающего за счет спина, запишем его в виде

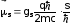(3.29)

èëè

[магнетон] = g_s (3.30)

ãäå g_s - безразмерная константа (спиновой гиромагнитный множитель), учитывающий отклонение собственного (спинового, а значит квантового) магнитного момента от классического (орбитального). В значении скрыта информация о структуре частицы. Можно показать (впервые это было сделано Дираком), что точечная заряженная частица со спином 1/2, массой m и зарядом q (например, электрон) имеет величину собственного магнитного момента

,

ò.å. äëÿ íå¸ =2. Отклонениеот этой величины для частицы со спином 1/2 говорит о внутренней структуре частицы. Экспериментальное определениеи их объяснение - важная задача субатомной физики.

Можно ввести, обобщая, и орбитальные гиромагнитные множители g_l, которые очевидно равны 1, например,

.

С помощью g_l можно включить в эту схему и нейтральные частицы, для которых 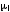=0, например, нейтрон, полагая для него

=0.

Магнитные моменты нуклонов и ядер выражают в ядерных магнетонах

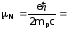3.1510^-18 ,

которые в =1836 раз меньше магнетона Бора

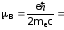5.7910^-15 .

Таким образом, магнитный дипольный момент ядра имеет орбитальную и спиновую составляющие:

. (3.31)

Гиромагнитные факторы (g-факторы) нуклонов даны в таблице 3.1.

Таблица 3.1