4. Ч¸тность. Орбитальная и внутренняя ч¸тность.

Ч¸тность системы частиц.

Инвариантность системы (гамильтониана ) относительно пространственного отражения - инверсии (замены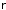-) приводит к закону сохранения ч¸тности и ещ¸ одному квантовому числу - ч¸тности. Ядерный гамильтониан обладает соответствующей симметрией.

Действительно,

, (3.7)

.

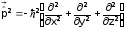Это означает, что система (ядро) не меняет своих свойств при -.

Определим оператор пространственной инверсии (оператор четности) для системы частиц следующим образом:

(3.8)

или просто ,

вводя обозначение .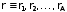

Подействуем на левую и правую части (3.8) ещ¸ раз оператором :

, (3.9)

ò.å. ² - оператор тождественного преобразования.

С другой стороны удовлетворяет уравнению на собственные значения (т.к. в силу инвариантности к пространственному отражению должно быть соответствующее сохраняющееся квантовое число):

= p. (3.10)

Из (3.9) и (3.10) следует, что

² = p² = ,

ò.å. p²=1 è p=1.

Итак, имеется две возможности

(3.11)

èëè

- четные функции (состояния),

- нечетные функции (состояния).

До сих пор волновая функция была волновой функцией системы точечных (бесструктурных) частиц. Вообще говоря, волновая функция частицы с индексом имеет вид

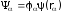, (3.12)

где описывает внутреннее состояние частицы , а - движение частицы как целого (точечного) объекта по некоторой траектории (орбите). Вид волновой функциив форме (3.12) следует из того, что гамильтониан объекта можно представить как сумму гамильтонианов, ãäåописывает объект как точку (без структуры), а- внутреннюю структуру объекта.

Оператор ч¸тности действует на каждый множитель в :

, (3.13)

причем, если - инвариантен к инверсии в пространстве внутренних координат,

, (3.14)

ãäå - внутренние координаты, а - внутренняя четность (операторв последнем соотношении совершает инверсию в пространстве внутренних координат частицы, от которых лишь и зависит ).

Волновая функция орбитального движения в центральном поле (т.е. движения с определенным l) может быть представлена в сферических координатах в виде

= R(r)Y_lm(™, ). (3.15)

Инверсия 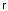-соответствует в сферических координатах преобразованию

r r

- (полярный угол) (3.16)

+ (азимутальный угол),

при котором радиальная часть волновой функции R(r) не меняется, а Y_lm(, ) - собственная функция оператора орбитального момента количества движения (так называемая сферическая функция или гармоника) - преобразуется следующим образом

Y_lm(, ) = (-1)^l Y_lm(, ). (3.17)

Итак, имеем

=(-1)^l . (3.18)

(-1)^l называется орбитальной четностью.

Волновую функцию системы независимых частиц можно представить в виде произведения волновых функций отдельных частиц

, (3.19)

ãäå = .

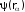Откуда, если речь идет о движении частиц в центральном поле,

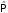(1, 2,..., A) = ₁₂..._A(1, 2,..., A).

Т.е. ч¸тность такой системы

. (3.20)

Для двух частиц

P₁₂ = ₁₂. (3.21)

В системе центра инерции l₁+l₂=L - орбитальный момент относительного движения.

Формулы (3.20)-(3.21) можно применять к ядру как системе нуклонов, рассматривая их как независимые частицы в общем ядерном потенциале, а также к реакциям, когда частицы до и после столкновения можно считать невзаимодействующими.

Имеют смысл лишь относительные внутренние четности. Для протона принимают _p=+1. Нейтроны имеют ту же внутреннюю четность +1. Остальные внутренние четности определяют относительно протона. Для электрона _e=+1. Для фотона =-1 (следствие того, что электромагнитное поле описывается векторным потенциалом 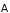, который эквивалентен волновой функции фотона, а для векторной функции

, (3.22)

что позволяет приписать фотону =-1).

Внутренние четности у частиц и античастиц с полуцелым спином (фермионов) противоположны, с целым спином (бозонов) - одинаковы.

Внутренние четности частиц получают из распадов и реакций с участием частиц с известной внутренней четностью на основе закона сохранения четности. Он имеет место в сильных и электромагнитных взаимодействиях и нарушается в слабых.

Íà ðèñ.3.1 демонстрируются принятые обозначения спина и четности ядерных состояний - , например 0⁺, 3/2^-, è ò.ä.