5. Сечение образования составного ядра нейтроном в

нерезонансной области

Получим выражение для сечения образования составного ядра. Будем предполагать, что сечение не зависит от квантовых чисел налетающей частицы и квантовых чисел составного ядра, и что уровни составного ядра образуют непрерывный спектр. Пусть падающая частица является нейтральной и не нужно учитывать кулоновское взаимодействие (например, случай образования составного ядра в реакциях с нейтроном). Вероятность образования составного ядра нейтроном определяется произведением вероятностей трех последовательных процессов:

1. Попадания нейтрона в область действия ядерных сил (эффективное сечение этого процесса обозначим );

2. Проникновения нейтрона внутрь ядра (вероятность этого процесса P);

3. Захвата ядром нейтрона (вероятность ).

Ядерные силы короткодействующие, поэтому можно считать, что они отличны от нуля только внутри ядра. Следовательно, сечение процесса, состоящего в том, что частица попадает в область действия ядерных сил, определяется выражением

₀ (R + 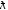)²,

где R - радиус ядра, - длина волны де Бройля для нейтрона. Зависимость потенциала, в котором движется налетающая частица, от расстояния между ней и центром ядра приведена рис.6.6.

Ðèñ. 6.6

При r=R происходит резкий скачок потенциала, связанный с тем, что в области r<R действуют ядерные силы, имеющие характер притяжения. При прохождении плоской волны через скачок потенциала возникает отраженная волна. Квантовомеханический расчет проницаемости барьера P для частиц с массой M, кинетичес-кой энергией T и орбитальным

моментом L=0 приводит к следующему результату

, (6.15)

ãäå ,.

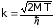В модели составного ядра считается, что частица, попав в ядро, с вероятностью =1 остается в нем (как уже отмечалось это имеет место для средних и тяжелых ядер и энергий нейтронов вплоть до нескольких десятков МэВ).

Таким образом сечение образования составного ядра нейтральной частицей (нейтроном) определяется выражением

_nÑ = ₀P (R +)². (6.16)

При высоких энергиях <<R è kk₀. Поэтому 1 è

получаем в качестве результата геометрическое сечение ядра

_nC R². (6.17)

6. Формула Брейта-Вигнера

Рассмотрим сечение образования составного ядра в районе изолированных уровней, т.е. когда ширины уровней меньше расстоянийE между ними. Изолированные уровни составного ядра отчетливо проявляются при рассеянии медленных нейтронов ядрами (рис.6.7). На этом рисунке показано сечение взаимо-действия нейтронов малых энергий (сотни эВ) с ядром²³⁸U. То, что наблюдаемые резонансы - уровни составного ядра, следует из их ширины.

Ðèñ. 6.7

Ширины показанных на рис.6.7 уровней (резонансов) после внесения поправок на аппаратную форму линии и допплеровское уширение оказываются 1 эВ. Это означает, что время жизни таких уровнейсек, что по крайней мере на 4 порядка превышает время пролета нейтрона с энергиями сотни эВ через ядро урана (это время 10^-19 - 10^-20 ñåê).

Экспериментальные данные показывают, что среднее расстояние между уровнями быстро уменьшается с ростом массового числа A и энергии возбуждения ядра. Это объясняется возрастанием числа различных способов распределения энергии между нуклонами. Все это приводит к тому, что с увеличением энергии нейтронов уровни начинают перекрываться.

Для тяжелых ядер это происходит уже для нейтронов с энергией T_n несколько кэВ. Энергия возбуждения составного ядра E* при этом близка к энергии отделения нейтрона из этого ядра B_n, равной нескольким МэВ (E*B_n+T_n для медленных нейтронов). Для высоких энергий возбуждения (15-20 МэВ) плотность уровней столь велика, что они, сильно перекрываясь, образуют непрерывный спектр. В этом случае процесс образования составного ядра имеет нерезонансный характер и к нему может быть применен подход, описанный в предыдущем разделе.

Итак, пусть у составного ядра C имеется набор изолированных уровней с энергиями пронумерованными в порядке их возрастания E_r=E₁, E₂,... . При совпадении энергии возбуждения этого ядра с энергией одного из уровней (E*=E_r) сечение образования составного ядра (a+AC*) и сечение реакции(a+AC*b+B) имеет максимум. Форма сечения в районе изолированного уровня совпадает с формой резонанса в механике, оптике и электричестве, т.е. с формой лоренцовой линии. В ядерной физике говорят о брейт-вигнеровской зависимости сечения от энергии. Формула Брейта-Вигнера имеет вид

_ab=, (6.18)

ãäå - де бройлевская длина волны падающей частицы.

Для реакции рассеяния нейтронов в районе изолированного уровня получаем

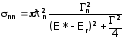. (6.19)

В этих формулах 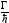- полная вероятность распада составного ядра в единицу времени;,,- вероятности распада составного ядра в единицу времени с вылетом частиц a,b и нейтрона.

= _a + _b + ... = . (6.20)

Из формулы Брейта-Вигнера можно получить сечение образования составного ядра _aC в области изолированного уровня

_ab = _aCW_b =_aC = . (6.21)

Откуда

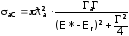. (6.22)

Ðèñ. 6.8

В заключение этого раздела рассмотрим область энергий составного ядра ниже самого первого резонанса (E*<E₁). В этой области (рис.6.8) сечение образования составного ядра нейтроном не имеет особенностей и можно воспользоваться формулой (6.16). Рассматриваемая область это область близких к нулю кинетических энергий нейтронов. Поэтому, полагаяè, получаем

_nÑ (R+)^{2 2} = , (6.23)

где v - скорость падающего нейтрона (k=v).