3. Кинематика ядерных реакций. Порог.

Рассмотрим реакцию

A + B C + D + ... (6.2)

Запишем закон сохранения энергии через массы и кинетические энергии T

(T_A + T_B) + (m_A + m_B)c² = (T_C + T_D + ...) + (m_C +m_D + ...)c².

Определим энергию реакции Q:

Q = (m_A + m_B)c² - (m_C + m_D + ...)c². (6.3)

И закон сохранения энергии запишем в виде

(T_A + T_B) = (T_C + T_D + ...) - Q. (6.4)

При Q>0 (выделение энергии) реакция идет при любом значении T_A+T_B, в том числе и нулевом (т.к. правая часть вышенаписанного соотношения может быть =0).

При Q<0 (поглощение энергии) реакция идет не всегда. Т. к. -Q>0, то для этого нужно T_A+T_B -Q =|Q|, т.е. чтобы T_A+T_B превышала разницу в массах конечных и начальных ядер. Таким образом, реакция обладает порогом, при котором начинает выполняться закон сохранения энергии.

Определение порога реакции E_ïîð: это минимальная суммарная кинетическая энергия сталкивающихся частиц (ядер), при которой реакция, идущая с поглощением энергии, становится возможной.

Оказывается

Eïîð = (TA+TB)min =

- ÑÖÈ (6.5) - ËÑÊ

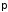Ниже покажем, что пороговые значения энергии в СЦИ и ЛСК равны величинам, приведенным в правой части выражения (6.5). E_ïîð зависит от системы координат. Она минимальна в СЦИ, где равна -Q=|Q|. Действительно, пороговая энергия минимальна когда (T_C + T_D + ...) =0, т.е. когда T_C=T_D= ... =0. Ïðè ýòîì p_C=p_D= ... =0, ò.å. (_C + _D + ...)=0, что отвечает определению СЦИ. В СЦИ центр инерции покоится и в частном случае может покоиться каждый из конечных продуктов. В остальных системах центр инерции движется и уже за счет этого T_C+T_D + ...0, т.е. часть кинетической энергии идет на бесполезную для реакции энергию движения центра инерции. При этом порог возрастает. Порогу в СЦИ отвечает рис.6.2.

Порог в сци

Ðèñ. 6.2

Теперь перейдем в систему координат, где B покоится, т.е. в ЛСК. Ситуация, которая отвечает порогу в этой системе, где скорость центра инерции v_öè (для простоты рассматриваем нерелятивистский случай), изображена на рис. 6.3.

Порог в ЛСК (T_B=0)

Ðèñ. 6.3

Èòàê, â ËÑÊ E_ïîð равно такому T_A, при котором продукты имеют нулевую относительную энергию (скорость), т.е. двигаются неразделенными. Ещ¸ раз отметим, что под ЛСК мы понимаем такую систему координат, в которой до взаимодействия объект B покоился (мишень), а объект A двигался (снаряд).

Найдем, используя релятивистские формулы, E_ïîð â ËÑÊ. Â ËÑÊ

E_ïîð = (T_A)_min = (T_A)_ïîð. (6.6)

Воспользуемся инвариантом I квадрата массы M системы частиц

M²c⁴. (6.7)

Запишем законы сохранения энергии и импульса в ЛСК и СЦИ и используем вышенаписанный инвариант:

ËÑÊ

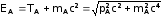
ÑÖÈ

Порогу в СЦИ отвечает рождение C, D, ... с нулевыми кинетическими энергиями, т.е.

; ; ...

.

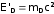Инвариант массы в ЛСК:

.

Отвечающий порогу инвариант массы в СЦИ:

()² - ()²c² = (m_C + m_D + ...)²c⁴.

Приравниваем инварианты массы в ЛСК и СЦИ и это отвечает

T_A = (T_A)_ïîð.

Имеем

(2T_A)_ïîðm_Bc² + (m_A + m_B)²c⁴ = (m_C + m_D +...)²c⁴.

Откуда

(T_A)_ïîð .

Пусть (m_C+m_D+...)²c⁴=b², à (m_A+m_B)²c⁴=a², тогда имеем (т.к. b-a=-Q=|Q|)

b² - a² = (b-a)(b+a) = |Q|(b + a + a - a) = |Q|(2a + |Q|)

Èòàê,

(T_A)_ïîð , (6.8)

причем два последних слагаемых в скобках - это доля кинетической энергии T_A, идущая на движение центра инерции.

В ядерной физике обычно |Q|<<2m_Bc² è

(T_A)_ïîð . (6.9)

При сохранении числа нуклонов |Q| - это разность энергий связи начальных и конечных продуктов.

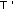Найдем (T_A)_ïîð в ЛСК в нерелятивистском приближении. В СЦИ из условия _ïîð = (_A + 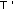_B)_min = -Q = |Q| имеем

Отсюда легко найти

; .

Переходя из СЦИ в ЛСК мы должны остановить частицу B, которая в СЦИ движется справа налево (рис.6.4). Это делается добавлением направленной вправо скорости 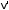_B каждой из двух частиц (A и B). Итак, ЛСК движется относительно СЦИ вправо со скоростью _B. Продукты C, D,... движутся в ЛСК в неразделенном виде со скоростью _B. Их кинетическая энергия бесполезна для реакции.

Ðèñ. 6.4

(T_A)_ïîð

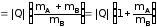. (6.10)

В нерелятивистском приближении доля кинетической энергии, идущая на движение центра инерции, равна 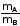. Добавкав формуле (6.8) связана с использованием релятивистских выраже-ний, т.е. существенна при высоких энергиях.

Пример. Найдем порог реакции +pp+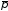+p в нерелятивистском и релятивистском приближении (- антипротон).

(T)_ïîð = |Q| = 2m_pc² =1877 МэВ. нерелят.

(T)_ïîð = 2m_pc² = 3754 МэВ. релят.

Т.е. релятивистская “поправка” удваивает порог.