
ЛЕКЦИЯ 6
Содержание
Ядерные реакции. Введение.
Законы сохранения в ядерных реакциях.
Кинематика ядерных реакций. Порог.
Механизмы ядерных реакций. Составное ядро.
Сечение образования составного ядра нейтроном в нерезонансной области.
Формула Брейта-Вигнера.
Прямые ядерные реакции.
1. Ядерные реакции. Введение.
Любой процесс столкновения элементарной частицы с ядром или ядра с ядром будем называть ядерной реакцией. Наряду с радиоактивным распадом ядерные реакции - основной источник сведений об атомных ядрах.
Для записи ядерной реакции есть несколько способов. Два наиболее употребительных поясняются следующими примерами
a + A b + B èëè A(a, b)B,
p
+

 +
+ èëè
èëè (p,
2), ãäå
(p,
2), ãäå
p
+
 n +
n +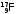 èëè
èëè (p,
n)
(p,
n)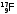 ,
,
+

 + p + n èëè
+ p + n èëè (,
pn)
(,
pn) .
.
Обычно более легкая частица называется - снарядом, более тяжелая -мишенью.
При
столкновении протона с
 могут быть различные процессы (каналы
реакции):
могут быть различные процессы (каналы
реакции):
|
|
p + 7Li |
- упругое рассеяние (упругий канал) | |
|
|
p + 7Li* |
- неупругое рассеяние |
|
|
p
+
|
+ |
|
|
|
|
+ + |
|
неупругие каналы |
|
|
p
+ + t, ãäå t |
| |
|
|
è ò. ä. |
|
|
Здесь 7Li* означает возбужденное состояние ядра 7Li.
При упругом рассеянии налетающая частица и мишень не претерпевают каких-либо внутренних изменений и не появляется новых частиц.
Первая ядерная реакция осуществлена в 1919 г. Резерфордом
+

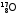 + p.
+ p.
Для
количественного описания вероятности
ядерной реакции используется эффективное
сечение - дифференциальное (d/d) и полное
( ). В случае двух частиц в начальном и
конечном состояниях реакция полностью
характеризуется d/d. Величина эффективного
сечения зависит от квантовых состояний
сталкивающихся частиц (энергий, спинов,
орбитальных и полных моментов, четностей,
изоспинов).
). В случае двух частиц в начальном и
конечном состояниях реакция полностью
характеризуется d/d. Величина эффективного
сечения зависит от квантовых состояний
сталкивающихся частиц (энергий, спинов,
орбитальных и полных моментов, четностей,
изоспинов).
Ядерные реакции рассматривают обычно либо в лабораторной системе координат (ЛСК), либо в системе центра инерции (СЦИ). ЛСК - система, в которой мишень покоится.
2. Законы сохранения в ядерных реакциях
Ряд физических величин одинаков до и после столкновения, т.е.
сохраняется. Имеют место следующие законы сохранения:
|
1. |
Энергии |
E |
|
2. |
Импульса |
|
|
3. |
Момента количества движения |
|
|
4. |
Электрического заряда |
Q |
|
5. |
Четности (за исключением слабого взаимодействия) |
P |
|
6. |
Изоспина (только в сильном взаимодействии) |
I |
|
7. |
Числа нуклонов (до порога рождения пары нуклон-антинуклон) |
|
|
8. |
Барионного заряда (сохранение числа нуклонов следствие этого закона) |
B |
|
9. |
Лептонного заряда |
L |
|
|
è äð. |
|
Выделены абсолютные или универсальные законы сохранения. Их нарушение никогда не наблюдалось.
Пример.
Найти конечное ядро x в реакции
+
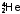 + x.
+ x.
Из
законов сохранения электрического
заряда и числа нуклонов получаем -
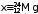 .
.
Пример на выполнение закона сохранения четности в сильных взаимодействиях: реакция 19F(p, )16O, идущая через возбужденное 1+ состояние промежуточного ядра 20Ne (ðèñ. 6.1).

Ðèñ. 6.1
Эта реакция идет за счет сильного взаимодействия с заселением 2-го возбужденного состояния ядра 16O, имеющего энергию 6.13 МэВ. Основное и 1-ое возбужденное состояния не заселяются. Почему?
Реакция проходит в две стадии:
p
+

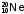 *(1+)
*(1+)
 +
+ (3-).
(3-).
Из закона сохранения углового момента для 2-й стадии
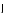 Ne
=
Ne
=
 O
+
O
+
 +
+ O,,
O,,
ãäå
 =
= ,
, O
=
O
= ,
, Ne=
Ne=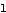 .
.
Для орбитального момента относительного движения ядра 16O и -частицы имеем
 =
= +
+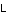 O,
и, опуская индексы, L=2, 3, 4.
O,
и, опуская индексы, L=2, 3, 4.
С другой стороны, из закона сохранения четности имеем
 (-1)L (6.1)
(-1)L (6.1)
èëè +1 = (+1)(-1)(-1)L.
Откуда остается лишь L=3.
Переход в основное и первое возбужденное состояние 16O невозможен, т.к. в этих случаях
 è
L=1.
è
L=1.
Но тогда не выполняется закон сохранения четности (6.1)
+ 1 (+1) (+1) (-1)L=1 = -1.
Опытным
путем установлено, что в рассматриваемой
реакции отношение вероятностей переходов
1+ 0+
è 1+
0+
è 1+ 3-
меньше 310-13,
что является хорошим подтверждением
справедливости закона сохранения
четности в сильных взаимодействиях.
3-
меньше 310-13,
что является хорошим подтверждением
справедливости закона сохранения
четности в сильных взаимодействиях.
