44. Доказать связь квадрупольного момента ядра со средней квадратичной деформацией.

Проведем расчет квадрупольного оператора . Аналогично расчету среднеквадратичного радиуса используем приближение точечных нуклонов для оператора плотности распределения заряда :

в приближении точечных нуклонов - следующая форма распределения заряда протонов:

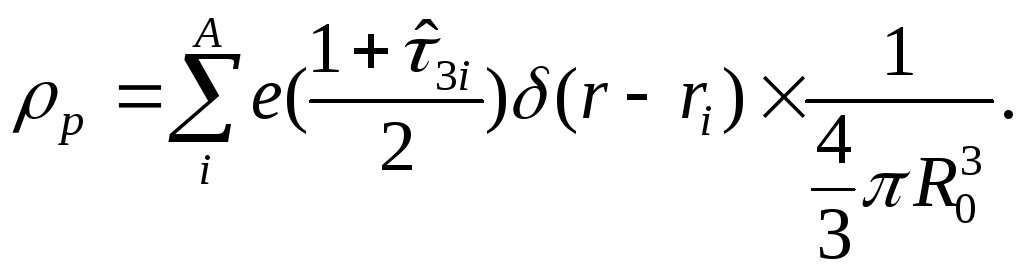
Интеграл имеет верхним пределом радиус поверхности ядра. В коллективных колебаниях он представляет собой динамическую переменную и зависит от амплитуды колебаний. Ограничиваясь квадрупольными колебаниями, имеем

В приближенных расчетах считают, что величина внутреннего квадрупольного момента ядра пропорциональна величине β₀,т.е.

45. Доказать, что приведенные на схемах (Субатомная физика стр.34) спектры возбуждения представляют собой "вращательные полосы".

Рассчитаем теоретические значения вращательных уровней Hf-180, подобрав значение

для уровня I=2:

То же самое для Dy-160 :

46. Рассчитать моменты инерции ядер Dy-160,Hf-180. Построить график

зависимости моментов инерции от энергий возбуждения.

Для Hf-180:

J	2	4	6	8
E,Mev	0.093	0.307	0.637	1.079
	0.093	0.214	0.33	0.442
	60	66	66	68

Для Dy -170:

J	2	4	6	8
E,Mev	0.087	0.284	0.528	0.972
	0.087	0.197	0.246	0.444
	69	71	89	68

47. Рассчитать моменты инерции ядер гафния в приближении твердотельного

ротатора; сравнить с результатами предыдущей задачи.

Для сферы:

• не все нуклоны учавствуют во вращении, крутится только холодное тело

• сверхтекучесть - св-во ядра в низших по энергии состояниях.

48. Привести пример вращательной полосы в спектре нечетного ядра.

Pu -239

49. Привести примеры вращательных полос с различными значениями К.

См. выше.

Энергетические уровни ядра.

Слева изображены все наблюдаемые уровни в энергетическом интервале 0-600 КэВ.

Справа приведено разбиение этих уровней на три вращательных полосы.

Энергетические уровни ядра .

Под каждой вращательной полосой указаны проекция K углового момента на ось симметрии и четность . Сверху над каждым вращательным уровнем указаны спин J и энергия возбуждения E соответствующего состояния. Уровень энергии 821.19 кэВ отвечает квадрупольным колебаниям деформированной ядерной поверхности.

50. Бекбендинг. Привести пример, дать качественное объяснение эффекта.

Таким образом, проведенный в № 47 несложный расчет доказывает, что ядро в низших возбужденных состояниях имеет значения момента инерции, составляющие не более 50% момента инерции твердого ротатора с той же массой. Часть нуклонов ядра оказывается не участвующей во вращательном движении вследствие эффекта спаривания нуклонов, приводящего к сверхтекучим свойствам ядер в основном и низших возбужденных состояниях. Разрыв нуклонных пар, происходящий при очень высоких моментах вращения ядер, проявляется в скачкообразном росте момента инерции ядра до величин близких к полученной выше твердотельной оценке. Этот эффект (т.н. бекбендинг = backbending) хорошо изучен в последние 20 лет на ускорителях тяжелых ионов. Исследование спектров возбуждения ядер проводится, главным образом, путем измерения энергий гамма-квантов, испускаемых ядром при переходе с более высокого уровня на более низкий по энергии.