Приложение к главе I Система единиц

В микрофизике, особенно в релятивистской, удобно работать с такой системой единиц, в которой мировые постояннные (постоян­ная Планка) и с (скорость света в вакууме) были безразмерны и равнялись единице:

=с=1. (I.1)

Поскольку обычная размерность есть эргсек, а скорости света см/cек, то выбор (I.1) предполагает, что

1 эрг = 1/сек^–1=1/c см^–1, (I.2)

1 см = 1/c сек.

Выбор (I.1) является наиболее простым, но можно его и не делать, а договориться измерять энергии, импульсы и т.д. в единицах с. Результат будет, естественно, один и тот же. Связь между энергией Е, импульсрм р, массой m в “обычной” (величины будут с индексом 0) и естественной системе единиц является следующей:

(I.3)

“Переводной” множитель

с = 1.9710^–11Мэвсм. (I.4)

В системе единиц (I.1) мы избавляемся от необходимости много раз писать в формулах константы и с. Рассмотрим несколько примеров.

Квадрат заряда протона (электрона) е²имеет размерность

[e²]=эргсм. (I.5)

Поскольку в системе (I.1) 1 эрг=1/с см^–1, то величина е²в этой системе является безразмерной:

. (I.6)

Массы m_N, m_нуклона и пиона равняются:

(I.7)

Для компактности записи мы ввели здесь внесистемную единицу “ферми”:

1 фм=10^–13см. (I.8)

Аналогичным образом фермиевская константа G_Fчетырех-фермионного слабого взаимодействия равняется

G_F=1.1710^–5 (Гэв)^–2 , (I.9)

а гравитационная постоянная

(I.10)

Характерная размерность G_N[см²] позволяет высказать гипотезу об элементарной гравитационной массе m_p(“планкион”) и элементарной длинне r_p:

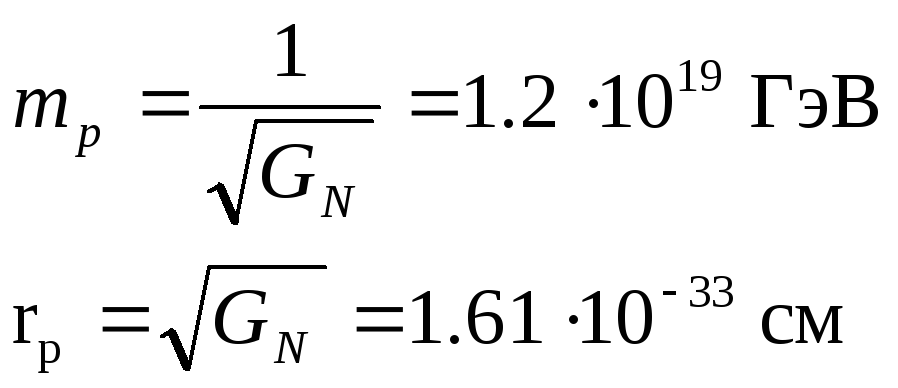(I.11)

Эффективные сечения

Эффективное сечение – либо дифференциальное d, либо полное_total– является характеристикой элементарного акта столкновения

a+b1+2+..., (II.1)

где а – налетающая частица, b – частица-мишень, 1,2,... – продукты реакции, т.е. частицы, появляющиеся в результате взаимодействия а и b. Эффективное сечене есть инвариантная величина в том смысле, что ее определение жестко связано с системой отсчета мишени (“лаборатор­ная система”), в которой мишень покоится. Договорившись об этом, можно находить в любой другой системе, соответствующим образом переопределяякинематические характеристики частиц. Рассмотрим сначала полное сечение_t.

Его определение связано с экспериментальной ситуацией, изображенной на рис. II.1.

Рис.II.1. Схематическое изображение экспериментов в микрофизике, тесно связанных с введением понятия сечения. В мишени указаны два акта.

Пусть N – полное число реакций, возникающих за времяt при прохождении потока частиц а через мишень, состоящую из частиц b. Пусть, далее, поток налетающих частиц заметно не уменьшается при прохождении мишени. Тогда полное сечение_tдается следующим выражением:

(II.2)

где v – объем мишени, j_a– плотность потока частиц а: j_a=n₁v₁и n₂– плотность частиц в мишени.

Из (II.2) видно, что _tимеет размерность см²и может быть истолковано как площадь элементарной площадки, сопоставляемой каждой частице-мишени, попадая в которую налетающая частица а обязательно вызывает реакцию. Используя то обстоятельство, что величина n/p₀является Лоренц-инвариантом, мы можем записать стоящее в знаменателе (II.2) произведение в виде:

(II.3)

где Лоренц-инвариант

. (II.4)

Величины n₁, n₂, p₁₀, p₂₀– плотности и энергии сталкивающихся частиц в произвольной системе отсчета; р₁, р₂– четыре-вектор частиц а и b:

. (II.5)

Соответственно, _tпримет вид:

. (II.6)

Поскольку tv есть элемент четырехмерного объема и является, следовательно, инвариантом, а числоN также есть инвариант, то формула (II.6) представляет собой релятивистско-инвариантную запись сечения.

Формула (II.6) может быть записана через полную квантово-механическую вероятность реакций w. Пусть w есть сумма плотностей вероятностей протекания всех реакций, возникающих при столкновениях а и b, отнесенных к условиям, когда в единице объема имеется одна частица а и одна b. Тогда

и

(II.7)

Здесь w_л– указанная вероятность в лабораторной системе, w – в произвольной системе отсчета.

Запись (II.6) позволяет, например, легко найти число N реакций, возникающих при столкновении встречных пучков. В этом случае

, (II.8)

где L=обычно называется светимостью системы встречнх пучков. При этом n₁, n₂– плотности пучков, р₁₀, р₂₀– их энергии,v – объем области столкновения.

Элемент сечения dвозникает в том случае, когда определяется плотность вероятности конкретной реакции с попаданием конечных частиц в элемент “фазового объема”. Элемент фазового объема dопределяется как число квантовых состояний конечных частиц в малых интервалах импульсов частиц dp_ii=1,2...

Из квантовой теории известно, что у одной частицы в фазовом пространстве dpV имеется

(II.9)

квантовых состояний, где V – объем, в котором заключена частица. Полагая V1 (так определяется вероятность w) и=1, получаем, что

(II.10)