§3. Симметрии см.

1. Говорят, что некоторый объект - физический или математический –симметричен по отношению к какому– либо проебразованию, если при этом преобразовании объект переходит сам в себя. Когда говорят о симметрии теории, то подразумевают, что при определенных преобразованиях ее динамических переменных уравнения теории не меняются и, следовательно, не меняется ее физическое содержание. Детальнее понятие “не меняется физическое содержание” будет рассмотрено позднее. Очевидно, что двухкратное преобразование симметрии есть снова преобразование симметрии – это важнейшее свойство, которое делает элементы преобразования группой. Группой в математике называют множество Gэлементовg, удовлетворяющих условиям:

g₁*g₂ =g₁₂,

g*g^-1=e, (1.67)

g*e=g,

где все g₁,g₂,g₁₂ G,e- единичный элемент,g^-1– элемент, обратныйg. Элементыgсуть указанные выше элементы симметрии. После введения понятия группы сказать, что объект обладает определенной симметрией, значит сказать, что он обладает определенной группой.

Группы могут быть дискретными и непрерывными. Элементы непрерывных групп нумеруются определенным набором параметров, пробегающих континуум значений. Пусть _i-набор параметров, характеризующих непрерывную группу. Тогда можно ввести инфинитоземальные операторы или генераторыt_iгруппы, определяемые формулой:

g() e –i ∑(t_k _k) . (1.68)

Поскольку элементы группы, вообще говоря, не перестановочны друг с другом, то генераторы должны удовлетворять некоторым коммутационным соотношениям типа:

[t_i,t_k] = ∑ c_ik^l t_l , (1.69)

где константы c_ik^lносят название структурных. Они зависят от параметризации группы и опредляются только ее структурой. Например, генераторыJ_iгенераторы группы вращений (группыSO₃, см. далее) удовлетворяют хорошо известным коммутационным соотношениям для момента количества движения:

[J_i ,J_k] = i_iklJ_l , (1.70)

где _ikl–единичный антисимметричный тензор. Как преобразуются динамические переменные физической системы и ее векторы состояния под действием группы, определяется конкретной симметрией. Ниже на нескольких примерах мы проследим

за этим действием генераторов и, следовательно, произвольных элементов группы.

2. Приведем несколько примеров важных для физики групп. Пара уравнений Максвелла, записанная в тензорном виде:

, (1.71)

где F^=^A^-^A^- тензор электромагнитного поля (A^-векторный потенциал), не меняется при преобразованиях Лоренца:

, (1.72)

где –матрица лоренцовских пребразований (при движении вдоль осиxмы получаем обычно приводимые в курсах физики матрицы преобразования Лоренца). Матрицылоренцовских преобразований – это матрицы 4x4, удовлетворяющие условиям:

,det=1, (1.72а)

где - транспонированная матрицаdet– детерминант,g=g_= 1,-1,-1,-1 метрический тензор пространства Минковского. При движении вдоль осиxматрицыпревращаются в обычно приводимые в курсах физики матрицы преобразования Лоренца. Нетрудно проверить, что множество матрицобразуют группу, которую и называт группой Лоренца. Соответственно, говорят, что уравнения (1.71) обладают группой Лоренца.

Аналогичным образом, уравнение Шредингера для бесспиновой частицы в сферически симметричном потенциале не меняет своего вида при повороте координат:

, (1.73)

где R– оператор поворота векторов. Это значит, что гамильтонианH(x) частицы не меняется при преобразованиях (1.73):

H(x)  H(x) = H(x) = H(x). (1.74)

Соответственно, уравнение Шредингера в новых переменных записывается в виде:

,(1.75)

где –преобразованная волновая функция:

(x) = (R^-1x). (1.76)

Операторы (матрицы) Rобразуют группу, которая называется группой вращений или группойSО₃. Соответственно говорят, что рассматриваемое уравнение Шредингера имеет группуSO₃.

Удобно групповые свойства уравнения Шредингера отобразить другим способом. Для этого введем оператор U(R), осуществляющий преобразование:

=. (1.77)

Преобразование (1.77) показывает, как действуют элементы группы на векторы состояния и на операторы динамических переменных.

Симметрия предполагает, что оператор Hгамильтона коммутирует со всеми операторамиU(R):

[H,U(R)] =0, (1.78)

и, соответственно, со всеми генераторами t_iгруппы вращений:

[Н,t_i]=0. (1.79)

Группа вращений задается тремя параметрами (например, углами Эйлера). Соответственно она задается тремя генераторами, в качестве которых обычно выбирают операторы t_i=J_i(i=1,2,3), гдеJ_i– операторы момента количества движения с коммутационными соотношениями (1.70)

Отображение элементов RгруппыSO₃на множество операторовU(R):

RU(R) , (1.80)

сохраняющее в терминах операторов U(R) основные свойства (1.67), на групповом языке называется представлением группыSO₃. Всегда можно найти векторное пространство, в котором операторы являются матрицами. В квантовой теории векторное пространство образуют векторы состояния. ОператорыU(R) - суть матрицы в этом пространстве векторов состояния, которое обычно называется гильбертовым пространством. И в общем случае отображение элементовgкакой - либо группыG(дискретной или непрерывной) на множество матрицU(g):

gU( g), (1.81)

действующих в пространстве векторов состояний, образует матричное представление группы G.

Представления групп бывают приводимыми и неприводимыми. Неприводимым называют такие представление, у которых нельзя уменьшить число преобразующихся друг через друга базисных векторов, переходя к новым векторам, являющихся линейными комбинациями прежних. Приводимое представление может быть разбито на инвариантные подпространства меньшей рамерности и может быть записано в виде прямой суммы неприводимых представлений. Соответственно, его матрицы U(g) могут быть представлены в блочном виде:

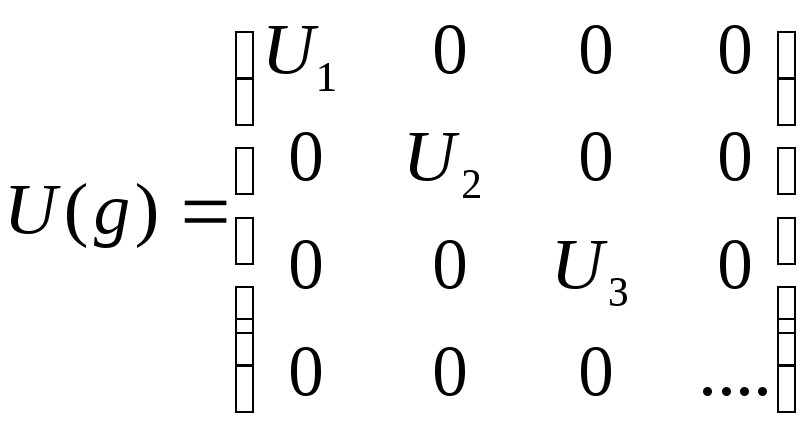, (1.82)

где U_i– теперь уже матрицы неприводимых прдставлений.

Применение теории групп к квантовой теории основывается на следующих трех положениях:

(1) группа предопределяет существование квантовых чисел, с помощью которых следует классифицировать квантово – механические состояния. Например, вращательная симметрия – группа SO₃- предполагает введение квантовых чиселJ,Mмомента количества движения и его проекции на ось квантования. Упоминавшаяся ранее изотопическая симметрия позволяет ввести квановое число изотопический спинI,I₃и т.д. С групповой точки зрения эти квантовые числа суть индексы, нумерующие матричные элементы представлений группы и определяются, вообще говоря, независимо от конкретного действия операторов группы на векторы состояния.

2. группа предопределяет законы сохранения квантовых чисел, введенных для классификации состояний. Например, симметрия относительно пространственных и временных сдвигов не только позволяет использование квантовых чисел E,P(энергии и импульса), но и приводит к их сохранению и т.д.

3. наконец, концепция локальных групп существенно облегчает построение разумных вариантов теории поля.

2. Стандартная модель обладает многими точными и приближенными симметриями. Наиболее простыми являются дискретные группы C,P,T– группы зарядового сопряжения, инверсии пространства и обращения движения. Все эти группы состоят из двух элементов – единичного и одного нетривиального, и на векторы состояниядействут следующим образом:

  _C(зарядовое сопряжениеC)

  _P(прстранственная инверсияP) (1.83)

  _T( обращение движенияT)

Операция С зарядового сопряжения сводится к замене в векторе состояния всех частиц на античастицы. При этом кинематические характеристики частиц не меняются. Например, при С- преобразовании вектор состояния частицы с импульсомпревращается в векторантичастицы с тем же самым импульсом.

Операция Р инверсии пространства сводится к изменению знаков всех импульсов:

 _P, (1.84)

где _Pпроизведение внутренных четностей частиц, каждая из которых может быть равной либо +1, либо –1.

Операция Т обращения движения производит следующее преобразование вектора состояния частицы:

 (-)^s--, (1.85)

где s–спин частицы,– его проекция на ось квантования в системе покоя частицы.

Замена “кэт” |> на “бра” < | при Tпреобразовании соответствует общей концепции обращения движения, при котором начальное состояние должно переходить в конечное. Подробнее и “доказательнее “ мы рассмотрим эти три операции в конце Гл.II. Здесь же мы только укажем, что квантовая электродинамика и квнтовая хромодинамика симметричны относительно всех трех операций в отдельности. Слабое взаимодействие оказывается несимметричной относительно каждой из трех операций. Подробнее речь об этом пойдет в Гл.III. Отметим, однако, что СМ симметрична относительно произведения всех трех операций, т.е. относительно СРТ - операции. Это утверждение носит название теоремы СРТ и является фундаментально важной ограничительной теоремой.

3.Рассмотрение непрерывных симметрий – непрерывных групп – СМ мы начнем с относительно простой группы SU₂, группы изотопической симметрии. Изотопическая группа и большинство из рассматриваемых далее групп являются симметриями КХД, составной части СМ. Преобразования изотопической группы касаются толькоu- иd- кварков и сводятся к их следующему преобразованию:

u  u +d, (1.86)

d  , ,

где

.

В матричном виде это преобразование записывается в виде:

; , (1.87)

где матрица U=является унитарной и унимодулярной, т.е. удовлетворяет соотношениям:

UU⁺ =1, det (U)=1 , (1.88)

и знак + означает эрмитовское сопряжение. Тяжелые кварки c,s,b,tи глюоны остаются при этом неизменными. То, что кварк- глюонный гамильтониан обладает изотопической группой означает, что физические свойства любой кварк- глюонной системы не изменяются, если перейти от степеней свободыu,dк степеням.

Существует и другая более наглядная формулировка изотопической симметрии. Именно, изотопическая симметрия –это симметрия гамильтониана с одинаковыми массами uиdи одинаковым взаимодействием пар кварков:

u-u , d-d , u-d (1.89)

При этом следует иметь в виду, что взаимодействие должно быть одинаковым в одинаковых состояних по относительному движению. Такое ограничение является очень важным, так как в системе u-dимеются состояния, которые отсутствуют (из-за принципа Паули) в системахu-uиd-d.

Группа SU₂ гомоморфна ( “эквивалентна”) обсуждавшейся выше группе пространственных поворотовSO₃. Поэтому математический аппарат группы формально совпадает с аппаратом группы вращений. Это значит, что изотопическая симметрия предполагает классификацию состояний по “моменту количества движния”Iⁱ, формальные свойства которого совпадают со свойствами оператора обычного моментаJⁱ . Этот оператор действует не на пространственные, а на кварковые переменные и называется изотопическим спином. Таким образом, изотопическая симметрия приводит к тому, что векторы состояния кварк-глюонных систем должны характеризоваться двумя квнтовыми числами – изотопическим спиномIи его проекциейI₃ на ось квантования. Эти квантовые числа могут принимать значения:

I= 0,1/2,1,3/2…, I₃ =-I,-I+1,...,I-1, I. (1.90)

С общей (групповой) точки зрения квантовое число Iявляется индексом неприводимого представления, аI₃– нумерует базисные векторы неприводимого представления.

К концепции изоспина можно подойти и по-другому. Преобразование (1.86) эквивалентно повороту обычного спина s=1/2, точнее преобразованию спиновых волновых функций частицы со спиномs=1/2:

, , (1.91)

где иопределяются углами поворота. Поэтому, можно считать, что кваркиuиd– суть состояния со спиномI=½ и его проекциями на ось квантования ±1/2. Изотопическая инвариантность теперь может быть сформулирована как инвариантность относительно поворотов изотопических спинов всех кварков в формальном "изотопическом пространстве". Поскольку имеет место полная аналогия с аппаратом обычного момента количества движения, то можно утверждать, что суммарный изоспин всех кварков

, (1.92)

где - изоспинk-го кварка.

Несколько дополнительных слов о включении в (1.92) изоспина антикварков. Нетрудно видеть из (1.86), что антикварки преобразуются как спиновые функции и –:

,. (1.93)

Поэтому в (1.92) можно подразумевать и суммирование по антикваркам, однако при конструировании сотояний с определенным полным изоспином необходимо учитывать связь (1.93) (см. задачу и §4). В заключение еще раз отметим, что изотопическая инвариантность связана с преобразованием только uиd– кварков. Более тяжелые кварки и глюны остаются при этом неизменными. Наиболее просто это обстоятельство можно учесть, приписав глюонам и тяжелым кваркам изоспин, равный нулю.

Как и в случае обычного момента количества движения изотопическая инвариантностьподразумевает независимость энергии от проекции изоспина I₃. Это означает, что массы

кварковых систем не зависят от I₃и что эти системы возникают мультиплетами с числом частиц в мультиплете 2I+1. Поэтому величина изоспинаIопределяется размерностью мультиплета. Обычно считается, что в пределах мультиплета проекция изоспина уменьшается с уменьшением заряда.

С концепцией изоспина мы встретимся в §4, Гл.III,IVиV. Здесь мы только укажем, что изотопическая инвариантность есть приближенная симметрия КХД. Точной она была бы только при равестве массuиd–кварков и пренебрежении кулоновским взаимодействием. Влияние этих факторов приводит к нарушению предсказаний изотопической симметрии на уровне процентов.

4.Следующей симметрией КХД является киральная симметрия. Киральная симметрия –это симметрия группы SU₂xSU₂, являющейся прямым произведением двух одинаковых группSU₂,т.е. симметрия двух независимых групп. Киральная симметрия, как и изотопическая, связана с преобразованиемuиd– кварков. В реальной КХД киральная симметрия является приближенной. Она была бы точной при нулевых массахuиdкварков. Рассмотрим, поэтому, идеальный случай нулевых масс кварков. В этом случае киральная симметрия – это симметрия относительно независимого преобразо- ванияuиd– кварков с разной спиральностью:

u₊₁ u₊₁ +  d₊₁ , d₊₁ –^* u₊₁ +^* d₊₁

u_-1 ^ u_-1 +^ d_-1 , d_-1 –^* u_-1 +^* d_-1 (1.94)

где , и ^’,^’ – два независимых набора параметров группы SU₂ ,u_1 и d_1 – состояния u и d кварков со спиральностями 1/2. Под спиральностью кварка мы понимаем проекцию спина на направление его движения. Независимость преобразования кварков с разными спиральностями означает, что левые и правые кварки образуют независимые подсистемы, и потому при киральной симметрии формируются две независимые и вырожденные группы адронов.

Реально массы u и d – кварков не равняются нулю (см. Таб. 1.2). Поэтому может показаться, что о киральной симметрии говорить не имеет смысла. Тем не менее, киральная симметрия имеет место и оказывает решающее влияние на формирование адронов

( см.§ 4). Выдающаяся роль киральной симметрии обусловлена тем, что эффекты КХД –взаимодействия оказываются намного большими массы u и d – кварков. Например, минимальная масса адрона – пиона -равняется около 140 МэВ, что намного больше масс u и d - кварков. Поэтому представляется вполне естественным, что на фоне обычных эффектов сильного взаимодействия массы кварков в первом приближении могут быть положены равными нулю.

Сделав такое предположение, мы, однако, сталкиваемся с новой сложностью. Киральная симметрия неизбежно приводит к тому, что спектр адронов должен быть двукратно вырожден. Действительно, предположение о двух независимых группах немедленно ведет к тому, что левые кварки, т.е. кварки с отрицательной спиральностью, формируют “свои левые адроны”, а правые, т.е. с положительной спиральностью, - еще один тип “правых” адронов. Поскольку четность в КХД сохраняется, то вместо правых и левых адронов при киральной симметрии должно возникать вырождение масс по четности. Между тем, массы реальных адронов ни в коей мере не являются вырожденными. Например, гипотетический киральный двойник нуклона- резонанс S₁₁ с характеристикой J=1/2^- - находится при энергии 1535 МэВ ( масса нуклона 940 МэВ). Нарушение киральной симметрии, обусловленное отличными от нуля массами u и d кварков (соответственно,4.5 и 7.5МэВ), должно давать лишь незначительные поправки и не может привести к расщеплению в 500 МэВ.

Решение этого парадокса в рамках СМ было найдено с помощью концепции спонтанного нарушения киральной симметрии. Спонтанное нарушение симметрии в действительности широко распространено в физике, и в данном случае состоит в следующем. Исходный гамильтониан КХД обладает группой SU₂ x SU₂ . В силу, однако, игры взаимодействий может реализоваться такая ситуация, когда основное состояние не обладает симметрией исходного гамильтониана. Как правило, это происходит в силу того, что в основном состоянии создается отличный от нуля “параметр парядка”, нарушающий симметрию исходного гамильтониана. Например, при спонтанном нарушении вращательной симметрии гамильтониана в ферромагнетике возникает параметр порядка в виде намагниченности в определенном направлении. В физике атомного ядра спонтанное нарушение симметрии происходит при возникновении несферичности ядер и т.д. В КХД спонтанное нарушение киральной симметрии связано с образованием конденсата кварк- антикварковых пар, т.е. макроскопического числа кварк-антикварковых пар в вакууме. Существование этого конденсата проявляется в отличном от нуля среднем значении по основному состоянию оператора рождения кварк – антикварковой пары:

<> 0, (1.95)

где суть операторы рождения кварков и антикварков. Можно убедиться ( мы сделаем это в следующем семестре) в том, что этот конденсат является кирально - неинвариантным объектом, и потому система, описываемая исходным кирально - симметричным гамильтонианом, тем не менее теряет эту симметрию. Таким образом, вследствие спонтанного нарушения киральной симметрии создается любопытная ситуация, когда гамильтониан остается кирально –симметричным, но тем не менее весь мир кварковых систем --адронный мир -- теряет такую симметрию из-за того, что основное состояние оказывается кирально несимметричным.

Эта ситуация является далеко не безобидной, приводя к ряду важнейших физических следствий. Мы укажем из них только два. Пожалуй, первым по значению является превращение токовых кврков в конституэнтные. Возникновение массы у конституэнтных кварков обусловлено отталкиванием токовых кварков от кварк- антикваркового конденсата. Вторым следствием является появление частиц с нулевой массой, которых называют “гольдстоуновскими” частицами. Считается, что такой частицей является пион. Предсказывается также ряд динамических следствий, например, соотношение Гольдбергера-Траймена между константами пион нуклонного взаимодействия и константой пионного распада. Детали смотрите в Гл.III.

5. Следующей по сложности является SU₃ – симметрия. В действительности есть две SU₃ – симметрии. Одна из них является точной и играет фундаментальную роль в формировании мира КХД и называется цветной SU₃ - симметрией. Она связана с преобразованием цветовых переменных. Другая играет подчиненную роль в том смысле, что квантово - хромодинамический мир великолепно мог бы существовать и без нее. Тем не менее, мы начнем именно с этой симметрии – флейворной SU₃ - симметрии, поскольку следующие из нее квантовые числа при первом знакомстве оказываются более понятными. Флейворная симметрия SU₃ состоит в следующем: гамильтониан КХД приближенно инвариантен относительно следующего преобразования трех кварков u, d, s:

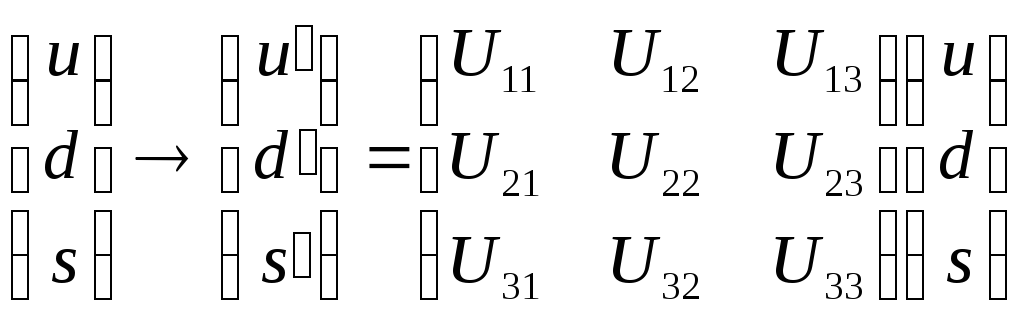, (1.96)

где матрица U удовлетворяет уже знакомым нам условиям:

det(U)=1,U⁺ U=1.

Формулировка (1.96) аппелирует скорее к математической конструкции гамильтониана, чем непосредственно к физическим образам. Поэтому мы приведем формулировку этой симметрии и в терминах “здравого смысла”. Именно, это симметрия гамильтониана, у которого, во-первых, являются одинаковыми массы кварков u, d, s и, во-вторых, являются одинаковыми взаимодействия в парах u-u, u-d, u-s, d-d, d-s, s-s.

Также как и изотопическая группа, SU₃ - симметрия предсказывает определенные квантовые числа, с помощью можно задавать векторы состояния кварковых систем. Однако в случае изотопической группы при выявлении этих чисел мы смогли ограничиться соображениями аналогии и здравого смысла, то здесь нам придется использовать уже терминологию теории групп и их представлений.

Как мы уже говорили, генераторы t_i любой непрерывной группы обязаны коммутировать с гамильтонианом кварковой системы. Поэтому собственное значение каждого из этих операторов сохраняется в процессе временной эволюции и может быть использовано для характеристики векторов состояния. Однако произвольно выбранные два генератора, вообще говоря, не коммутируют друг с другом, и, следовательно, все генераторы не могут использоваться для определения состояния. Чтобы указать систему коммутирующих генераторов, воспользуемся явным определением (1.96) группыSU₃ как матричной группы. Обычно эти генераторы выбираются в виде t_i = 1/2_i , где матрицы _i называются матрицами Гелл-мана и имеют следующий вид:

, ,,,,

. (1.97)

Среди матриц t_i имеется две матрицы t₃ и t₈, коммутирущиe друг с другом. Кроме них есть еще одна билинейная комбинация генераторов – =t₁² +t₂² +t₃², коммутирующая с t₃ и t₈. В результате мы имеем три коммутирующих друг с другом оператора, собственные значения которых I, I₃ и переопредленное квантовое число Y= (1/3) t₈ , называемое гиперзарядом, могут нумеровать векторы состояния |  > = | I, I₃ ,Y> .

Операторы t₃, t₈ и коммутируют между собой, но не со всеми другими генераторами. Есть, однако, еще два независимых оператора – их называют операторами Казимира, являющиеся функциями генераторовt_i, но которые, тем не менее, коммутируют со всеми генераторами t_i. Простым примером оператора Казимира является оператор квадрата полного момента количества движения, который, как хорошо известно, коммутирует с операторамиJ₁,J₂, J₃ проекций момента. Естественно включить два собственных значения операторов Казимира в число квантовых чисел, задающих состояние. Вместо этих собственных значений обычно используются два других числа (m,n) c mn и m,n = 0,1,2,….При заданных числах m,n число различных векторов состояния

| (m,n);I, I₃,Y> равняется

N = ½ (m+1)(n+1)(m+n+2). (1.98)

Таким образом, мы приходим к заключению, что симметрия SU₃предсказывает, что векторы состояния любой кварковой системы могут быть заданы пятью квантовыми числами (m,n),I,I₃,Y.

С групповой точки зрения собственные векторы | (m,n);I, I₃,Y> образуют неприводимое представление группы SU₃. Индексы (m,n) нумеруют неприводимые представления, индексы I, I₃,Y нумеруют базисные векторы неприводимого представления. Под действием элементов группы эти векторы преобразуются друг через друга следующим образом:

| (m,n);I, I₃,Y> (m,n);I, I₃,Y=|, (1.99)

где - матрицы неприводимого представления. Некоторые из таких матриц приводятся в справочниках.

Нетрудно понять, что при наличии SU₃ – симметрии так же, как и в случае изотопической симметрии, кварковые системы возникают (как собственные функции гамильтониана) “мультиплетами” частиц с одинаковой массой. Число частиц в мультиплете определяются тем, какова размерность неприводимого представления с данными (m,n).

Действительно, введем оператор E, который с одной стороны является линейной комбинацией генераторов t_i , а с другой “пересчитывает” векторы | (m,n);I, I₃,Y> неприводимого прдеставления (m,n) ( построение такого оператора возможно, см.книги по теории групп). В случае группы вращений таким оператором является, например, оператор J₊ = J_x + iJ_y ). Это значит, что начиная с некоторого базисного вектора, мы можем действием оператора Е получить все другие векторы, принадлежащие данным (m,n). Поскольку оператор Е коммутирует с гамильтонианом H (он строится из генераторов!), то имеет место следующая цепочка равенств:

H|> = m|>, EH|> =m E|> = HE |>,

HE|> = m E|>, (1.100)

т.е. состояние Е|> принадлежит той же массе, что и |>, где | > == | (m,n);I, I₃,Y> -некоторый базисный вектор.

Изложенное есть все, что может дать симметрия SU₃ для решения проблемы классификации состояний частиц. Симметрия, однако, приводит к ряду динамических следствий, т.е. к ряду соотношений между различными реакциями. Эти и другие следствия мы рассмотрим в Гл.V

Из-за разности масс u и d –кварков и s- кварка флейворная симметрия SU₃ является сильно нарушенной. Тем не менее, очень полезные следы этой симметрии остаются, и они играют важную роль в адронной физике.

Рассмотрим, наконец, цветную SU₃ – группу. Преобразования этой группы состоят в смешивании цветов глюонов и цветов кварков внутри каждого аромата,например:

(1.101)

g_a  g_a =U_a,a g_a , (1.102)

где u_1,2,3 – кварки аромата u с цветами 1,2,3 , g_a – восьмерка глюонов с цветом a и U_a,a матрица 8x8, согласованная с матрицей преобразования кварков. Матрицы U_a,a образуют в терминологии математиков сопряженное представление группы SU_3..

Разумеется, с концептуальной точки зрения в цветной структуре кварковых систем нет ничего нового: аналогичные флейворной группе квантовые числа состояний, аналогичные законы сохранения. Однако реальный аппарат цветной группы существенно упрощается за счет того, что структура основного состояния КХД такова, что состояния с отличным от нуля цветом не допускаются. Это значит, что любое допустимое состояние КХД всегда должно быть бесцветным, т.е. инвариантом, или, что то же обладать нулевыми квантовыми числами (m=0,n=0). Это и есть определение понятия бесцветного состояния. В большинстве практических случаях требование бесцветности сильно упрощает конструкцию кварковых состояний (см. §4). Присутствие глюонов даже при условии бесцветности существенно усложняет конструирование состояний.

Цветная группа SU₃ является группой строгой симметрии и накладывает на динамику

кварков, глюонов и адронов глубокий отпечаток. К настоящему времени не все следствия цветной природы КХД до конца поняты.

6. До сих пор мы молчаливо предполагали, что рассматриваемые группы являются глобальными группами. Это значит, что фундаментальные степени свободы преобразуются одинаковым образом во всем пространстве. Между тем на фундаментальном уровне требование одинаковости преобразования во всех точках пространства является нелогичным. Откуда мы знаем о том, какие параметры групп выбраны для фиксации цветов кварков и глюонов, например, в туманности Андромеда? Фундаментальный уровень требует скорее локальных групп – неизменности теории при “своем” выборе параметров преобразования в каждой точке пространства – времени. Концепция локальных групп оказалась чрезвычайно плодотворной. Чтобы сформулировать эту концепцию и понять вытекающие из нее следствия, необходимо перейти к языку теории поля, поскольку в ней работают с операторами ,зависящими от пространственно – временных координат.

Пусть (x) – есть полевая функция ( “поле”), описывающая фундаментальные фермионы, т.е. частицы со спином 1/2. Будем, далее, подразумевать под (x) столбец кварковых полей:

(x) =,

где индексы 1,2,3 определяют цвет кваркового поля. Потребуем теперь локальности цветной SU₃ симметрии теории. Это значит, что теория должна быть инвариантной относительно преобразования:

(x) (x) = U(x) (x), (1.103)

или в матричном виде

= , (1.104)

где t_k – введенные ранее генераторы цветной группы, _к - параметры этой группы, зависящие от пространственно временной точки. Выыражение представляет собой общее выражения для матрицыU(x). В уравнениях для поля (x), какими бы они не были, обязательно должны входить производные ^(x). Инвариантность теории, однако, сразу же нарушается преобразованием производных. Действительно, имеет место очевидное несоответствие членов с производными в преобразованных и непреобразованных уравнениях:

^ (x) = (^ +i^ t_k _k(x)) (x) ↔ ^(x). (1.105)

Практически единственный способ компенсировать лишний член i^ t_k _k(x) = i^(x) это ввести в производную ^ векторные поля A^_a , т.е. заменить ^^+ iА^ с законом преобразования векторного поля:

A^ A^ =S A^S^-1 +i(^S) S^-1. (1.106)

Здесь А^ = t_k A^_k ,  = t_k _k , S =. В результате при преобразования (1.104) множитель факторизуется:

(^ +i A^)(x) = (^ +i A^ ) (x) (1.107)

и имеет место инвариантность относительно (1.104).

Таким образом, требование локальной группы почти автоматически приводит к необходимости введения векторных полей, число которых должно равняться числу генераторов группы ( при группе SU₃ число таких полей равняется восьми – отсюда восемь глюонов) . В СМ имеется всего две локальные группы – SU₂x U₁ и цветная SU₃.

Первая из них лежит в основе электрослабой теории, и предполагает существование “праполей” триплета А^_а и синглета B^. Подробнее это будет рассмотрено в Гл. III.