Семинар 7.
Функции от случайной величины.
Пусть
задано вероятностное пространство
;
пусть на нём задана действительная
функция
,
которая является случайной величиной
с множеством значений
.
Предположим на множестве
задана действительная функция
,
такая, что
.
В этом случае
будет случайной величиной. Причём , если
– дискретна, то
тоже дискретна.
Пример 1.
Найти
закон распределения с.в.
,
где
имеет распределение Пуассона с параметром
.
Величина
принимает два значения:
Пример 2.
Найти
функцию и плотность распределения
случайной величины
,
где
распределена нормально с параметрами
0 и 1.
Отсюда плотность будет следующей:
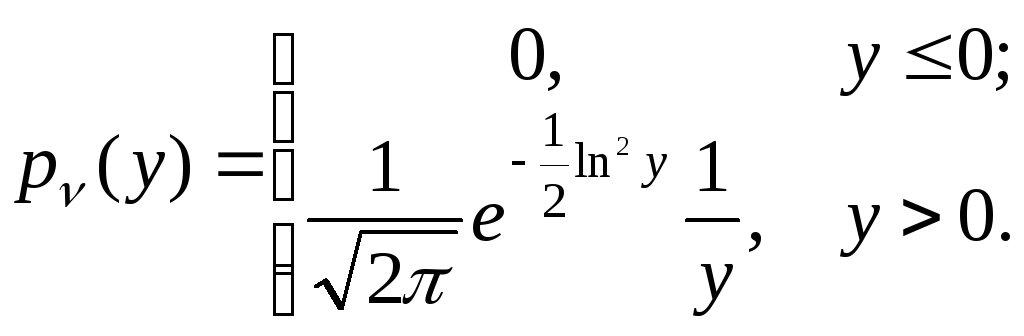
Математическое ожидание функции от случайной величины.
Пусть
– случайная величина. Для нахождения
числовых характеристик случайной
величины не обязательно знать функцию
распределения. Математическое ожидание
будет следующим:
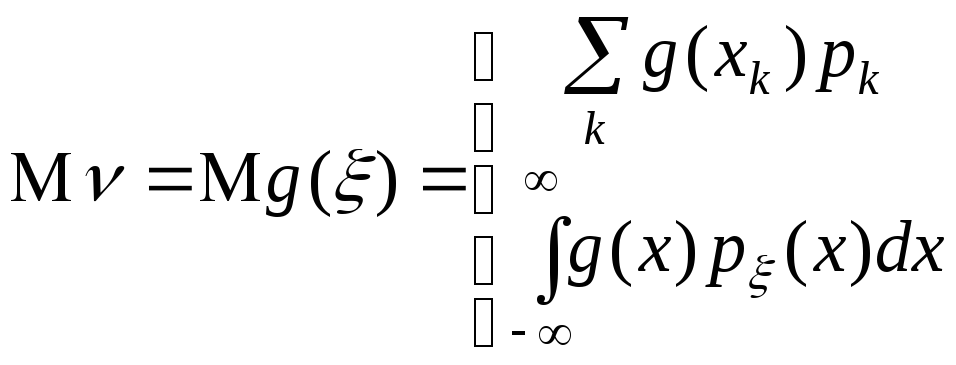
Математическое ожидание считается существующим, если существует абсолютное математическое ожидание.
Математические ожидания от некоторых функций имеют собственное название:
– начальный
момент k-ого
порядка;
– центральный
момент k-ого
порядка.
Свойства математического ожидания.
1. 
-
-
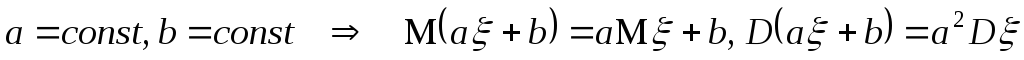
Неравенство Чебышева:
Характеристические функции.
Случайные величины можно характеризовать не только функцией распределения, но и характеристическими функциями, а именно:
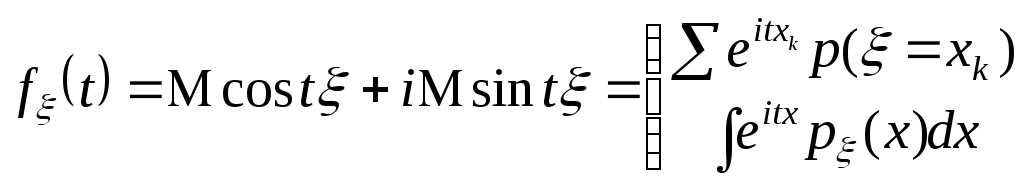
Свойства характеристических функций.
-
Характеристическая функция любой случайной величины существует при всех действительных значениях t, причём
. -
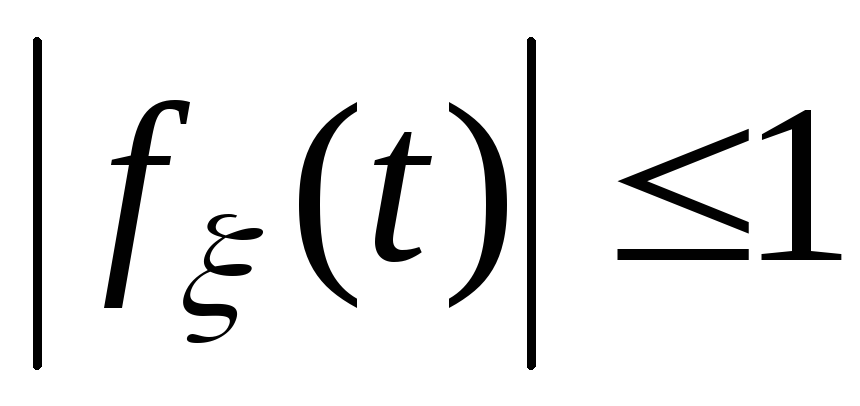Действительная часть х.ф. – чётная функция, а мнимая часть – нечётная функция.
-
-
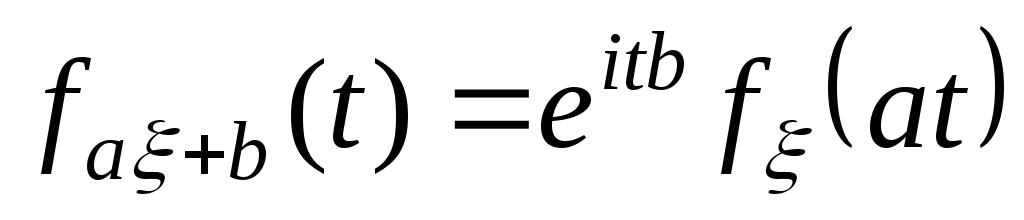
Если существует k-ый начальный момент случайной величины, то характеристическая функция k раз непрерывно дифференцируема на всей числовой прямой, и:
-
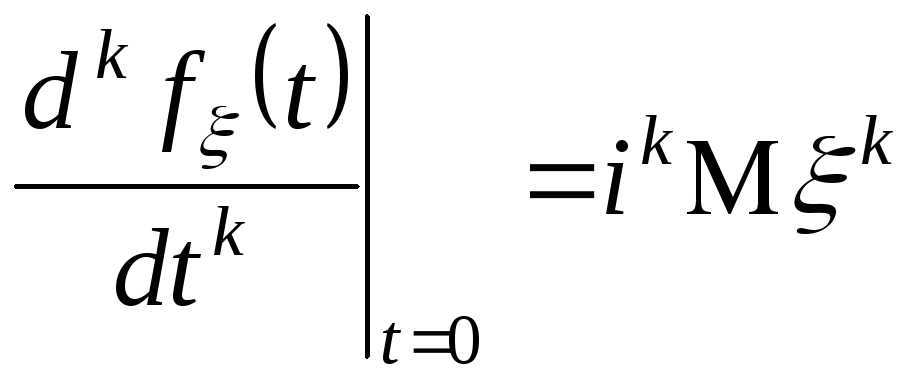
Если х.ф. абсолютно интегрируема, то:
Задача 10.1.
Найти характеристические функции следующих распределений:
а) равномерного в интервале [-а, а]:
б) биноминального:
г)
распределения Коши:
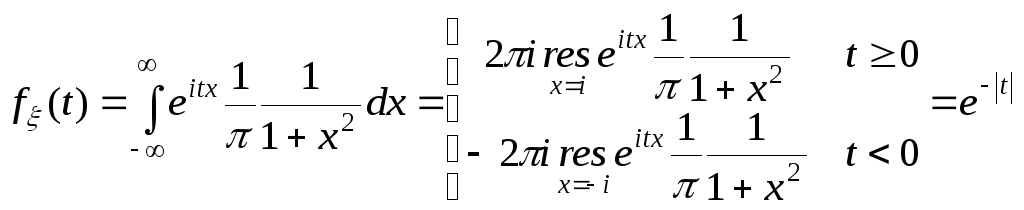
Задача 10.4.
Доказать, что следующие функции не могут быть характеристическими функциями:
а)
, 
;
б) вещественная функция не обладающая свойством чётности;
в)
г)
Центральная предельная теорема.
В случае повторения одного и того же опыта большое количество раз, можно установить общие закономерности относительно результата всей совокупности измерений, а именно справедлива следующая теорема:
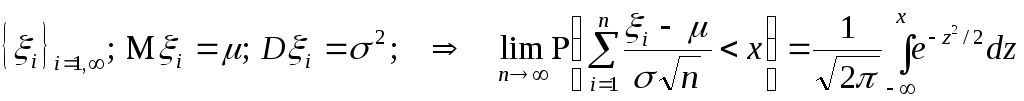
Задача 10.7.
Игральная кость подбрасывается до тех пор, пока общая сумма выпавших очков не превысит 700. Оценить вероятность того, что для этого потребуется более 210 бросаний? менее 180 бросаний? от 190 до 210 бросаний?
Найдём
сначала математическое ожидание и
дисперсию для каждого бросания
;
В первом случае очевидно при 210 бросаниях будет общая сумма будет менее 700, то есть
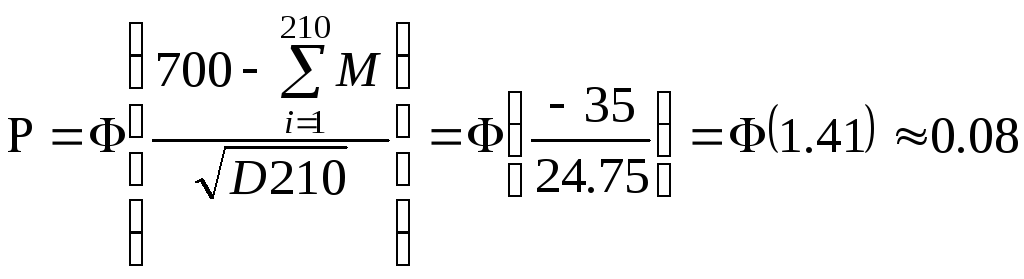
Во втором случае при 180 бросаниях общая сумма будет более 700 очков, то есть:
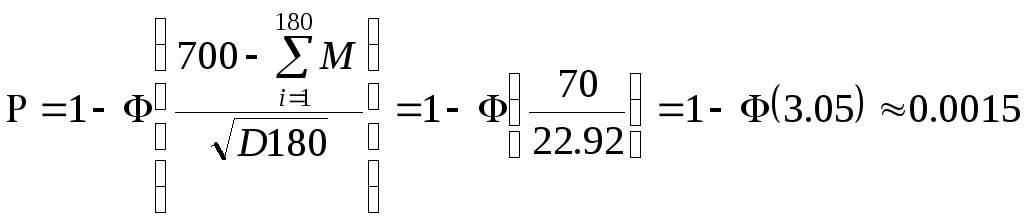
В третьем случае при 190 бросаниях сумма будет менее 700 очков, а при 210 бросаниях больше, то есть:
