Семинар 4.
1. Распределение Пуассона.
Расчёт вероятностей
в биноминальной схеме при больших
затруднителен. Но в случае малой
вероятности
успеха, можно оценить вероятность
какого-либо события следующим образом.
Предположим, что
и
,
тогда
.
Обозначим
,
распределение вероятностей приобретает
вид:
.
Данная формула для вычисления вероятности
называется распределением Пуассона.
Причём, так как
,
то данное распределение вероятностей
можно брать в качестве вероятностной
меры при построении каких-либо
вероятностных пространств. В распределении
Пуассона используется параметр
,
который, как видно, равен некоторому
среднему числу успехов в серии из
испытаний, иными словами этот параметр
равен ожидаемому числу успехов, где под
понимается не вероятность, а частота
успеха.
Пример 5.2:
Книга в 500 страниц содержит 50 опечаток. Оценить вероятность того, что на случайно выбранной странице не менее 3 опечаток.
Решение:
Можно ожидать, что
на одной странице встретится 0.1 опечаток,
причём количество букв на одной странице
велико, таким образом можно воспользоваться
распределением Пуассона с параметром
.
По другому, вероятность встретить
опечатку при проверке одной буквы равна
,
где
– число букв на странице. Проверяется
букв, причём
,
то есть можно воспользоваться
распределением Пуассона. Искомая
вероятность будет равна:
Пример 5.4:
Сколько изюма в среднем должны содержать калорийные булочки для того, чтобы вероятность иметь в булочке хотя бы одну изюмину была не менее 0.99?
Решение:
Пусть в среднем
булочки содержат
изюмин. Тогда искомая вероятность будет
,
по условию она должна быть больше 0.99.
Таким образом
Пример 5.7:
Предположим,
что при наборе книги существует
вероятность
того, что любая буква может быть набрана
неправильно. После набора гранки
прочитывает корректор, который
обнаруживает каждую опечатку с
вероятностью
.
После корректора – автор, обнаруживающий
каждую из оставшихся опечаток с
вероятностью
.
Найти вероятность того, что в книге со
ста тысячами печатных знаков останется
после этого не более 10 незамеченных
опечаток.
Решение:
Для начала нам нужно найти вероятность успеха в одном испытании, в данном случае – это вероятность того, что останется опечатка.
Обозначим 
– буква набрана с опечаткой,
– корректор её исправил,
– опечатку исправил автор,
– опечатка осталась.
Тогда нам требуется
найти
.
Очевидно, что
,
отсюда
и
Искомая вероятность
будет
2. Локальная и интегральная предельная теоремы Муавра-Лапласа.
Для биноминального
распределения существуют с помощью
формулы Стирлинга
можно получить приближённую формулу:
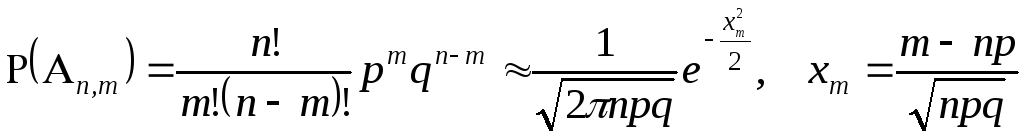
Данная формула называется локальной предельной теоремой Муавра-Лапласа.
Но при большом
числе испытаний, как правило бессмысленно
говорить о событии, заключающемся в
наступлении ровно
успехов. События, для которых имеет
смысл искать вероятность, – это интервалы.
Иными словами, такие события заключаются
в том, что число успехов лежит в некотором
интервале. Для таких интервальных
событий справедлива интегральная
предельная теорема Муавра-Лапласа:
.
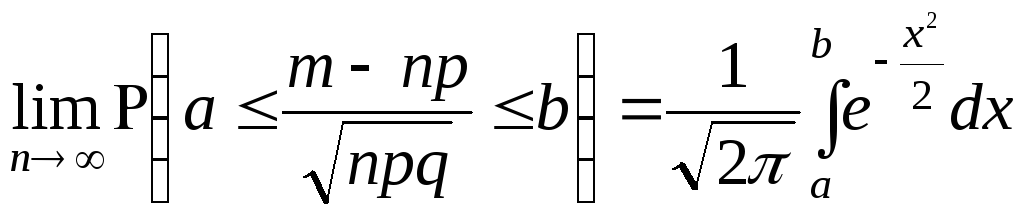Где
называется интегралом ошибок.
Пример 6.1:
Известно, что вероятность рождения мальчика приблизительно равна 0.515. Какова вероятность того, что среди десяти тысяч новорождённых мальчиков будет не больше, чем девочек?
Решение:
Пример 6.2:
Для лица, дожившего до 20-летнего возраста, вероятность смерти на 21-ом году жизни равна 0.006. Застрахована группа в 10000 человек 20-летнего возраста, причём каждый застрахованный внёс 1.2 рубля страховых взносов за год. В случае смерти застрахованного страховое учреждение выплачивает наследникам 100 рублей. Какова вероятность того, что:
а) к концу года страховое учреждение окажется в убытке;
б) его доход превысит 6000 рублей; 4000 рублей?
а)
б)
в)
