Семинар 1.

1. Вероятностная модель эксперимента.

1.1. Пространство элементарных событий.

Для эксперимента со случайным исходом, в первую очередь необходимо указать все элементарные исходы, которые могут произойти в результате эксперимента, подразумевается, что может и обязательно происходит только один элементарный исход. Элементарные исходы обычно обозначают . Совокупность элементарных исходов называют пространством элементарных исходов, обозначают обычно . Любой результат эксперимента это точка множества , в случае, если можно считать, что ни один из элементарных исходов не является предпочтительным, можно приписать каждому элементарному исходу вероятность , то есть для нахождения вероятности необходимо найти число элементарных исходов.

Пример 1. Однократное подбрасывание монеты.

Пример 2. При -кратном подбрасывании монеты.

Пример 3. Выбор без возвращения, есть пронумерованных предметов, из них случайным образом вынимается штук.

– упорядоченные выборки

– не упорядоченные выборки

Пример 4. Выбор с возвращением, есть пронумерованных предметов, из них случайным образом вынимается штук, при этом каждый раз предмет кладётся обратно, запоминаем только номер.

– упорядоченные выборки

неупорядоченные выборки.

Доказательство:

Воспользуемся индукцией .

и

Пусть

Вообще в эксперименте может быть интересен не конкретный исход, который имеет место в результате эксперимента, а принадлежность исхода какому-нибудь подмножеству пространства элементарных исходов. Все те подмножества , для которых по условиям эксперимента возможен однозначный ответ о принадлежности элементарных исходов этому подмножеству называются событием. По другому, событие – это совокупность тех , которые влекут .

1.2. Алгебра событий.

Предположим, что мы знаем пространство элементарных исходов и у нас есть некоторые представления о вероятности каждого элементарного исхода, а нам нужно найти вероятность какого-нибудь события. Например, подкидываем монету 10 раз, какая будет вероятность, что ровно 3 раза выпадет орёл. Для того чтобы найти вероятности событий на их множестве вводят алгебраические операции.

Объединение или сумма

Дополнение или противоположное

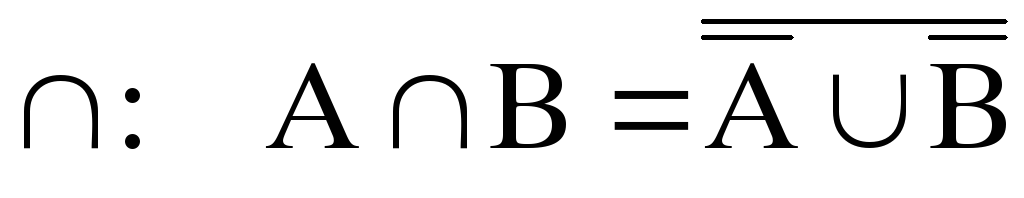Пересечение или произведение

Следствие

Невозможное событие

Достоверное событие

Разность

Симметрическая разность

Теория вероятности имеет дело с множеством событий , называемым алгеброй, удовлетворяющим следующим условиям:

2. Классическая теоретико-вероятностная модель

Припишем каждому элементарному событию (исходу) некоторый "вес" , называемый вероятностью исхода , совокупность вероятностей должна удовлетворять условиям не отрицательности и нормировки.

Вероятность заданного события определяется:

Тройка , где , – некоторая алгебра подмножеств , определяет вероятностную модель, или вероятностное пространство.

Свойства:

Формула Стирлинга

3. Задачи по §1.

1.1.

1.4.