
Семинар 3.
1. Условная вероятность.
Тройка
![]() называется вероятностным пространством,
если выполнены следующие 5 условий:
называется вероятностным пространством,
если выполнены следующие 5 условий:
-
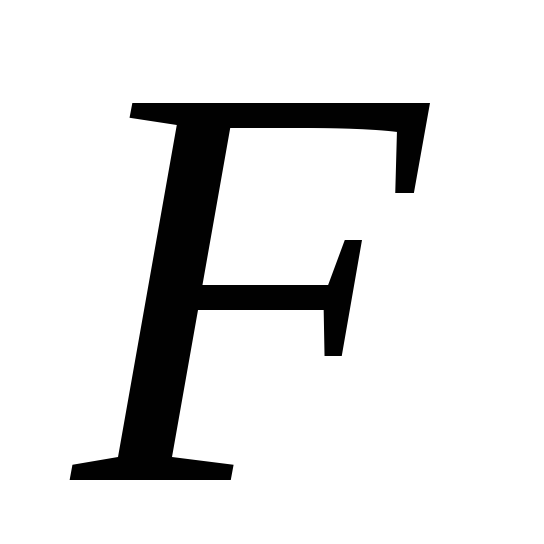 –
–
 -алгебра,
то есть
-алгебра,
то есть

-
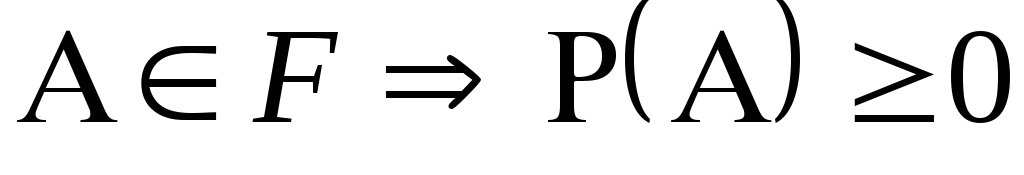 Вероятность
определена для любых событий из алгебры.
Вероятность
определена для любых событий из алгебры. -
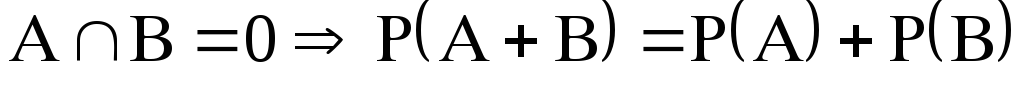 Аддитивность
вероятности
Аддитивность
вероятности -
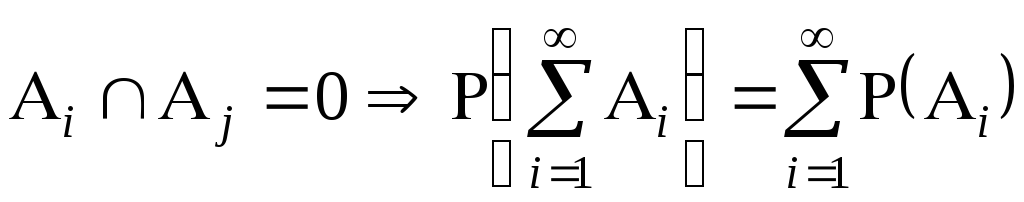 Сигма аддитивность
вероятности
Сигма аддитивность
вероятности -
 Нормированность
вероятности.
Нормированность
вероятности.
Предположим, нам
известно, что произошло некоторое
событие
![]() и нам требуется узнать вероятность
некоторого другого события
и нам требуется узнать вероятность
некоторого другого события
![]() .
Например, при игре в карты вы знаете
только свои карты, и хотите узнать
вероятности раскладов остальных карт.
В таком случае вводят понятие условного
вероятностного пространства
.
Например, при игре в карты вы знаете
только свои карты, и хотите узнать
вероятности раскладов остальных карт.
В таком случае вводят понятие условного
вероятностного пространства
![]() ,
где
,
где
![]()
![]()
![]()
Замечание.
Предполагается, что
![]()
Свойства условной вероятности.
-
Вычисление вероятности пересечения событий.
Формула умножения
вероятности
![]()
![]()
![]()
![]()
-
Формула полной вероятности.
Пусть задана полная
группа событий, то есть
![]() .
Тогда
.
Тогда
![]()
-
Формулы Байеса.
![]()
Для полной группы
событий, то есть
![]()
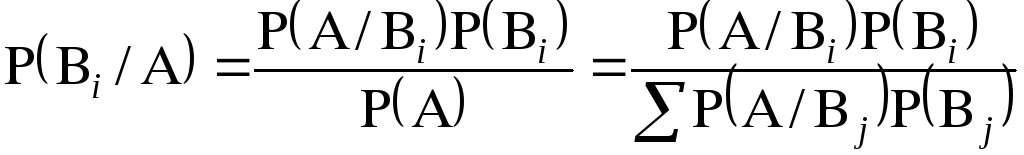
2. Независимость событий.
События называются
независимыми, если
![]() .
.
Если события
независимы, то независимы также следующие
пары
![]()
В терминах условной вероятности это определение эквивалентно следующим:
![]()
![]()
Примеры:
3.1 Студент пришёл на экзамен, зная лишь 20 из 25 вопросов программы. Экзаменатор задал студенту 3 вопроса. Используя понятие условной вероятности найти вероятность того, что студент знает все вопросы. Найти ту же вероятность, используя классическое определение вероятности.
Решение: Нам нужно
найти вероятность одновременного
наступления трёх событий
![]() ,
по формуле вероятности пересечения
событий получаем
,
по формуле вероятности пересечения
событий получаем
![]() ,
а по формулам классической вероятности:
,
а по формулам классической вероятности:
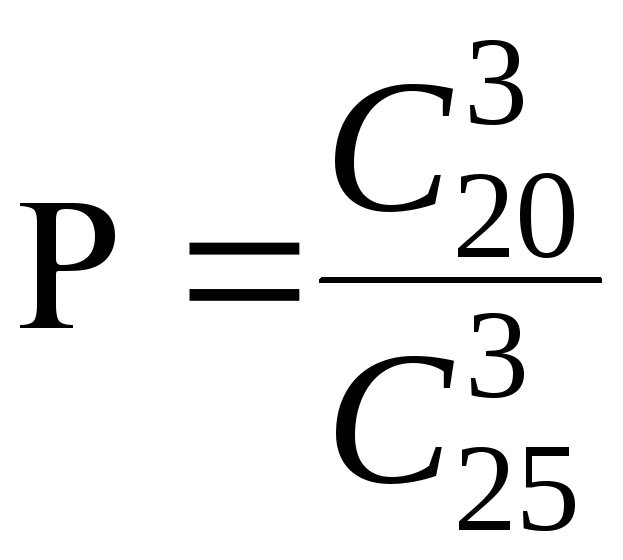
3.4 Стрелок
![]() поражает мишень с вероятностью
поражает мишень с вероятностью
![]() ,
стрелок
,
стрелок
![]() – с вероятностью
– с вероятностью
![]() и стрелок
и стрелок
![]() – с вероятностью
– с вероятностью
![]() .
Стрелки дали залп по мишени и две пули
попали в цель. Что вероятнее: попал
.
Стрелки дали залп по мишени и две пули
попали в цель. Что вероятнее: попал
![]() или нет?
или нет?
Решение: По условию
попали двое, обозначим
![]() – событие, заключающиеся в том, что
попали двое.
– событие, заключающиеся в том, что
попали двое.
![]()
![]()
![]()
![]() Таким образом,
вероятнее, что
Таким образом,
вероятнее, что
![]() попал.
попал.
3.8
Вероятность того, что письмо находится
в письменном столе, равна
![]() ,
причём с равной вероятностью оно может
быть в любом из восьми ящиков стола.
Просмотрели семь ящиков и письма не
нашли. Какова вероятность, что письмо
в восьмом ящике?
,
причём с равной вероятностью оно может
быть в любом из восьми ящиков стола.
Просмотрели семь ящиков и письма не
нашли. Какова вероятность, что письмо
в восьмом ящике?
Решение: Обозначим
![]() – в семи ящиках нет письма,
– в семи ящиках нет письма,
![]() письмо есть в восьмом и
письмо есть в восьмом и
![]() письма нет в столе. Тогда, искомая
вероятность будет равна
письма нет в столе. Тогда, искомая
вероятность будет равна
![]() ,
очевидно, что вероятность письму
отсутствовать в нижних ящиках при
условии, что оно есть в верхнем, равна
единице. Таким образом
,
очевидно, что вероятность письму
отсутствовать в нижних ящиках при
условии, что оно есть в верхнем, равна
единице. Таким образом
![]() .
.
3.16 Из урны, содержащей 3 белых и 2 чёрных шара, переложены два вынутых наудачу шара в урну, содержащую 4 белых и 4 чёрных шара. Найти вероятность вынуть из второй урны белый шар.
Решение: Введём
обозначения
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Здесь буквы обозначают последовательность
вынимания шаров из первой урны. Видно,
что эти события образуют полную группу,
таким образом
.
Здесь буквы обозначают последовательность
вынимания шаров из первой урны. Видно,
что эти события образуют полную группу,
таким образом
![]() .
Найдём входящие в сумму вероятности.
.
Найдём входящие в сумму вероятности.
![]()
![]()
![]()
![]()
![]()
3. Последовательность независимых испытаний.
Рассмотрим некоторый
случайный эксперимент
![]() .
Пусть он содержит конечное число
элементарных исходов:
.
Пусть он содержит конечное число
элементарных исходов:
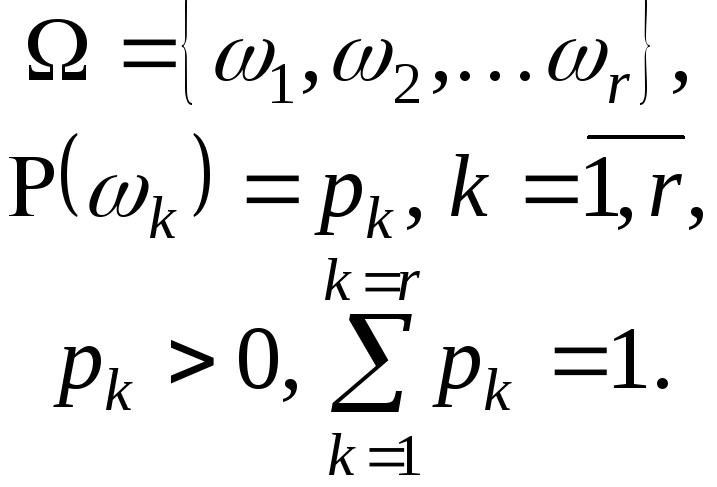
Предположим, что
данный случайный эксперимент повторен
![]() раз. Тогда новый эксперимент можно
описать следующим вероятностным
пространством
раз. Тогда новый эксперимент можно
описать следующим вероятностным
пространством
![]() :
:
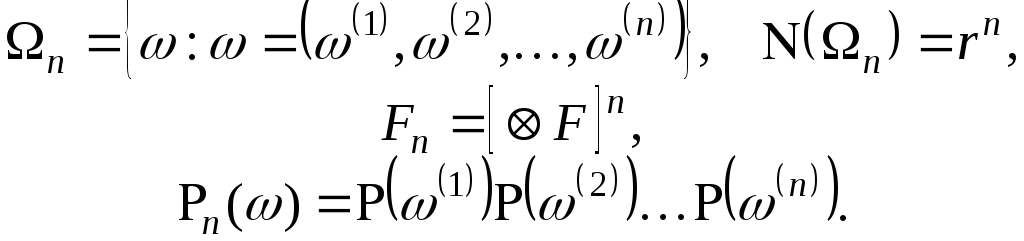
Для построенного нового вероятностного пространства выполняются все аксиомы вероятностного пространства.
Если
![]() ,
то схема независимых испытаний называется
биноминальной схемой, в остальных
случаях полиномиальной схемой.
,
то схема независимых испытаний называется
биноминальной схемой, в остальных
случаях полиномиальной схемой.
В рамках биноминальной
схемы приняты следующие обозначения
![]() .
При этом
.
При этом
![]() называется успехом, а
называется успехом, а![]() неудачей. Основное событие, которое
рассматривается в данной схеме, это
вероятность ровно
неудачей. Основное событие, которое
рассматривается в данной схеме, это
вероятность ровно
![]() успехов в серии из
успехов в серии из
![]() испытаний. Вероятность каждого
элементарного исхода равна
испытаний. Вероятность каждого
элементарного исхода равна
![]() ,
а всего таких элементарных исходов
будет
,
а всего таких элементарных исходов
будет
![]() ,
таким образом
,
таким образом
![]() .
.
Помимо биноминальной
схемы можно рассмотреть отрицательную
биноминальную схему или распределение
Паскаля. Основное событие в этой схеме
– для достижения
![]() успехов потребовалось
успехов потребовалось
![]() испытаний. Для подсчёта искомой
вероятности заметим, что последним
результатом должен быть обязательно
успех, в противном случае
испытаний. Для подсчёта искомой
вероятности заметим, что последним
результатом должен быть обязательно
успех, в противном случае
![]() -ый
успех будет достигнут раньше. Таким
образом
-ый
успех будет достигнут раньше. Таким
образом
![]()
Для полиномиальной схемы очевидно будет
![]()
Примеры:
4.2 Для того, чтобы узнать, сколько рыб в озере, отлавливают 1000 рыб, метят их и выпускают обратно в озеро. Потом 150 раз отлавливают по одной рыбе и снова выпускают в озеро. При каком общем числе рыб в озере будет максимальной вероятность встретить среди 150 отловленных рыб 10 меченых.
Решение: Задача
отвечает биномиальной схеме независимых
испытаний, в которой успех есть
отлавливание меченой рыбы. Всего
проведено
![]() испытаний, успехов
испытаний, успехов
![]() .
Вероятность успеха в единичном испытании
равна доле меченых рыб среди всех рыб
в озере, т.е.
.
Вероятность успеха в единичном испытании
равна доле меченых рыб среди всех рыб
в озере, т.е.
![]() где
где
![]() – общее число рыб,
– общее число рыб,
![]()
Найдем
![]() .
Очевидно, что
.
Очевидно, что
![]() ,
на котором достигается максимум по
,
на котором достигается максимум по
![]() функции
функции
![]() и
есть искомое решение. Дифференцируем
по
и
есть искомое решение. Дифференцируем
по
![]() и приравниваем производную нулю. Получаем
уравнение для определения
и приравниваем производную нулю. Получаем
уравнение для определения
![]() :
:
![]() .
Отсюда
.
Отсюда
![]()
4.3 Допустим, что
вероятность попадания в цель при одном
выстреле равна
![]() ,
а вероятность поражения цели при
,
а вероятность поражения цели при
![]() попаданиях в неё
попаданиях в неё
![]() .
Какова вероятность того, что цель
поражена, если было произведено
.
Какова вероятность того, что цель
поражена, если было произведено
![]() выстрелов.
выстрелов.
Решение: Введём
обозначения
![]() – цель поражена,
– цель поражена,
![]() –
–
![]() попаданий в мишень. Тогда
попаданий в мишень. Тогда
![]()
![]()
![]()
4.9 Ведётся стрельба
до первого попадания. Выстрелы независимы
и вероятность попадания при каждом
выстреле равна
![]() .
Какова вероятность того, что потребуется
6 выстрелов, если известно, что было
сделано чётное число выстрелов?
.
Какова вероятность того, что потребуется
6 выстрелов, если известно, что было
сделано чётное число выстрелов?
Решение: Введём
обозначения
![]() – потребовалось
– потребовалось
![]() выстрелов, где
выстрелов, где
![]() – произвольное чётное число,
– произвольное чётное число,
![]() – потребовалось чётное количество
выстрелов. Очевидно, что
– потребовалось чётное количество
выстрелов. Очевидно, что
![]() .
Тогда искомая вероятность будет
.
Тогда искомая вероятность будет

Для нахождения
входящих в это выражение вероятностей
воспользуемся отрицательной биноминальной
схемой с
![]() :
:
![]()
Таким образом искомая вероятность будет:
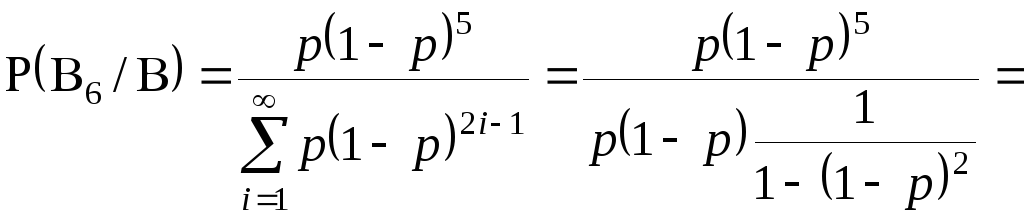
![]()
