сиаод / Otvety_Saod

Узел имеющий 2 сына называется двухместным. Узел имеющий три сына называется трехместным.

Высота 2-3 дерева, содержащего n узлов, не может быть больше [log(n+1) - 1] (целая часть).

2-3 дерево поиска.

Ключи размещаются в соответствии со следующими правилами:

1 Двухместный внутренний узел имеет двух сыновей. Ключ двухместного узла должен быть больше, чем ключи левого поддерева и меньше, чем ключи правого поддерева.

2 Трехместный узел имеет трех сыновей. Должен содержать два элемента данных. Ключ S больше TL, но меньше TM, а ключ L больше, чем TM, но меньше TR.

3 Лист может содержать один или два элемента данных.

34. Обход 2-3 дерева.

Node2-3Tree = (S, L, Left, Middle, Right)

Обход:

Алгоритм InOrder(R) 1 if (R-лист) then

2 Обрабатываем элементы в узле R

3 else if (R – трехместный) then

4InOrder(R^.left)

5Обработать первый элемент

6InOrder(R^.middle)

7Обработать второй элемент

8InOrder(R^.right)

9Обработать третий элемент

10InOrder(R^.left)

11Обработать элемент узла

12InOrder(R^.right)

13end if

14end if

Поиск:

Алгоритм Retrieve(R, key, elem) 1 if (key R) then

2 elem  данные, содержащиеся в узле R

3 return true

4else

5if (R – лист) then return false

6 else if (R – трехместный) then

7 if (key < R.S) then

return Retrieve(R^.left, key, elem) 8 else if ( key < R.L) then

return Retrieve (R^.middle, key, elem)

9 else return Retrieve (R^.right, key, elem)

10 end if

11 end if

12else

13if (key < R.S) then

14return Retrieve(R^.left, key, elem)

15else return Retrieve (R^.right, key, elem)

16end if

17end if

18end if

35. Добавление элемента в 2-3 дереве.

Алгоритм вставки:

1 Нужно найти лист, на котором прекращается поиск этого элемента 2 Вставить элемент в этот узел. Если после вставки лист содержит 3 элемента – выполнить разделение:

Разделение внутреннего узла:

Разделение корня:

Алгоритм Insert (R, newelem)

1 присвоить key ключ newelem

2 найти лист leafnode, но который можно разместить ключ key

3 добавить элемент newelem в лист leafnode  newelem

4 if (leafnode содержит три элемента) then Split (leafnode)

Алгоритм Split(n)

1 if (n – корень) then

2 создать новый узел p

3 назначить узел p родителем n

4 end if

5 создать два новых узла n1, n2 и назначить их родителем узел p 6 в узел n1 записать меньший ключ из n

7 в узел n2 записать больший ключ из n 8 if (n – не является листом) then

9 n1 – родитель двух левых сыновей n

10 n2 – родитель двух правых сыновей n

11 end if

12 перенести средний ключ в узел p

13 if (p содержит 3 элемента) then Split(p)

Эффективность – О(log(n))

36. Удаление элемента в 2-3 дереве.

При удалении ключа из узла возникают три варианта.

1)Если после удаления ключа в узле содержится два ключа, то после удаления ничего не меняется.

2)Если же у ключа после удаления остался один элемент, то проверяем количество потомков второго ребенка того узла, ребенком которого является узел с удаляемым ключом. Если у него два ребенка, то присваиваем ему оставшийся один элемент. Вершину, оставшуюся без детей, удаляем рекурсивно.

3)Иначе у него три ребенка. Тогда присваиваем узлу с одним ключом один из этих ключей, таким образом получая два узла с двумя ключами.

Алгоритм удаления Delete(r, key) 1 Найти позицию элемента key 2 if (elem – не лист) then

3 Поменять местами найденный элемент с симметричным приемником

4 end if

5 удаляем элемент elem из leafnode

6 if (leafnode – пуст) then Fix(leafnode)

Алгоритм Fix(n)

1 if (n – корень) then

2 удалить корень

3else

4установить p на родительский узел узла n

5if (брат узла n содержит два элемента) then

6выполнить перераспределение между n, братом и p

7if (n – внутренний) then

8переместить соответствующий доч. узел от брата к n

9 end if

10else

11установить s на брата n

12перенести из p в s

13if (n – внутренний) then

14присоединить доч. узел узла n к s

15end if

16удалить n

17if (p – пуст) then Fix(p)

18end if

19end if

37. 2-3-4 деревья. Основные свойства.

Узел может быть 2-х, 3х и 4-х местным. 4. узел содержит 1-2-3 эл-та данных.

Type Node = ^pNode pNode = record key: TypeT0; left, leftmiddle, rightmiddle, right: pNode. End.

Поиск проводится как и в 2-3 дереве.

1TL < S; TR > S

2TL < S; S < TM < L; TR > L

3TL < S; S < TML < M; M < TMR < L; TR > L

Свойства четырехместного узла: 1 может быть корнем

2 может иметь три сына и два элемента данных

3 может иметь четыре сына и три элемента данных

Максимальная высота 2-3-4 - дерева h=(log2n+1), и вставка нового элемента, как правило, не изменяет ее за исключением случая, когда разделяется корень дерева.

38. Добавление элемента 2-3-4 дерево.

Разделение четырех местного узла (остальное как в 2-3 дереве) 1 Корень

2 Родитель двухместный

3 Родитель трехместный

39. Сортировка. Стратегии внутренней сортировки.

Вспомним задачу сортировки в общем виде. Даны элементы a1 , a2 ,..., an . Сортировка означает перестановку этих элементов в порядке ak1 , ak2 ,..., akn , так что при заданной функции

упорядочения справедливо отношение f (ak1 ) f (ak2 ) ... f (akn ) .

1)Выборка – выбирают наименьший элемент и помещают в текущую позицию в выходном потоке.

2)Включение – элементы орабатываются по одному в произв порядке, вставка нового Элта в соотв с отношением его к уже имеющимся 3)Обмен – Эл-ты сравниваются и при необходимости меняются местами пока не будут упорядочены.

4)Распределение – Эл-ты распределяются по подмножествам (младшие – в одно, старшие

– в другое, промежуточные – в промеж)

5)Слияние – сортироанные подмножества объединяются в более крупные, исп-я методы слияния.

40. Турнирная сортировка.

Этот метод сортировки получил свое название из-за сходства с кубковой системой проведения спортивных соревнований: участники соревнований разбиваются на пары, в которых разыгрывается первый тур; из победителей первого тура составляются пары для розыгрыша второго тура и т.д. Алгоритм сортировки состоит из двух этапов. На первом этапе строится дерево: аналогичное схеме розыгрыша кубка.

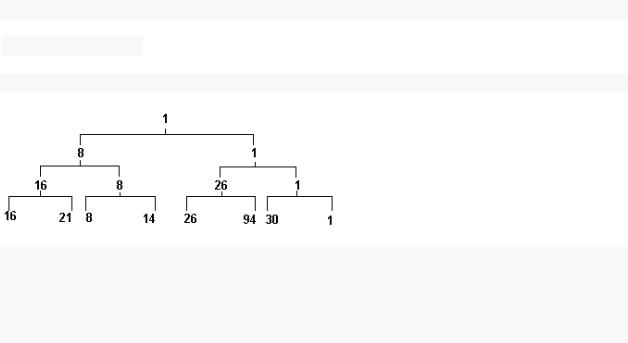
Например, для последовательности чисел a:

16 21 8 14 26 94 30 1

такое дерево будет иметь вид пирамиды, показанной на рисунке:

В примере приведена программная иллюстрация алгоритма турнирной сортировки.

Алгоритм:

Строится двоичное дерево (глубина 2к≥n) сортируемых ключей: 1.все ключи листья

2.из пар выбирается мин и становится узлом порядка k-1, процесс продолжается пока корнем дерева не станет мин эл-т 3.переправляем этот эл-т в исходную последовательность

4.спускаемся по дереву и заменяем значения мин элемента на + 5.все промежуточные узлы заменяем минимальными из оставшихся.

6.процесс продолжается до тех пор пока все листья не будут заменены фиктивными ключами

Число сравнений (n-1)log2n: время работы O(log2n)

41. Пирамидальная сортировка.

Пирамида – бинарное дерево, в узлах ключи сортируем по значениям данных. - Неубывающая; -Невозрастающая;

Метод простого выбора. N(n-1) сравнений, n-1 перестановок. Пирамидальная сортировка (сложность nlogn, неустойчивый алгоритм)

Дерево называется пирамидально упорядоченным, если ключ в каждом его узле ≥ ключам всех его потомков. Сортирующее дерево – совокупность ключей, образующих полное пирамидально упорядоченное дерево. Для реализации дерева используется массив([i/2]- родитель, 2i, 2i+1- потомки). При такой организации прохождение по дереву проходит более быстро с большой экономией памяти. Поддержание осн св-ва пирамид дерева.

Heapify(A,i)

L:=left[i]

R:=right[i]

If l =< Heap-Size(A) &A[l]>A[i] Then largest:=l

Else largest:=r

If (r=<Heap-Size(A) & (A[r]>A[largest) Then largest:=r

If largest<>I then begin

A[i]<–>A[largest]

Heapify(A,largest) End

Построение пирамиды

Build-Heap(A) Heap-Size:=length(A)

For i:=[length(A)/2] downto 1 do Heapify(A,i)

Сортировка

HeapSort Build-Heap(A)

Fori:=length(A) downto 2 do A[1]<->A[i] Heap-Size(A):=Heap-Size(A)-1 Heapify(A,1)

42. Вставка с убывающим шагом (метод Шелла).

Рассматриваются пары с шагом h/2, если элем не упорядочены, то меняем их местами. Рассматриваются группы с шагом h/4, выполняем сортировку в группах,

уменьшаем шаг и т.д. Проходим по всему массиву. Простая вставка n2/4 – вычислительная сложность. Вычислительная сложность O(n(logn)2)

Пример: Для примера возьмем 16 элементов [1..16]. Сначала просматриваются пары с шагом 8. Это пары элементов 1-9, 2-10, 3-11, 4-12, 5-13, 6-14, 7-15, 8-16. Если значения элементов в паре не упорядочены по возрастанию, то элементы меняются местами. Назовем этот этап 8- сортировкой. Следующий этап - 4-сортировка, на котором элементы в файле делятся на четверки: 1-5-9-13, 2-6-10-14, 3-7-11-15,4-8-12-16. Выполняется сортировка в каждой четверке. Сортировка может выполняться методом простых вставок (п.1). Следующий этап - 2- сортировка, когда элементы в файле делятся на 2 группы по 8:

1-3-5-7-9-11-13-15 и 2-4-6-8-10-12-14-16. Выполняется сортировка в каждой восьмерке. Наконец весь файл упорядочивается методом простых вставок.

ShellSort(x, n, hs, s) For i: = s downto 1 do H:=hs

For j:=h+1 to n do begin Y:=x[j]

k:=j-h

while (k>=1) and (y<x[k]) do begin x[k+h]:=x[k]

k:=k-h end x[k+h]:=y end;

end;

43. Быстрая сортировка.

Среднее время работы . Время работы алгоритма для массива из элементов в

худшем случае может составить , на практике этот алгоритм является одним из самых быстрых.

Алгоритм:

из массива выбирается некоторый опорный элемент .

запускается процедура разделения массива, которая перемещает все ключи,

меньшие, либо равные , влево от него, а все ключи, большие, либо равные — вправо.

 для обоих подмассивов: если в подмассиве более двух элементов, рекурсивно запускаем для него ту же процедуру.

Быстрая сортировка

//алгоритм на языке java и с//с++

public static void qSort(int[] A, int low, int high) { int i = low;

int j = high;

int x = A[(low+high)/2]; // x - опорный элемент посредине между low и

high

do {

while(A[i] < x) ++i; // поиск элемента для переноса в старшую

часть

while(A[j] > x) --j; // поиск элемента для переноса в младшую

часть

if(i <= j){

// обмен элементов местами: int temp = A[i];

A[i] = A[j]; A[j] = temp;

// переход к следующим элементам: i++; j--;

}

} while(i < j);

if(low < j) qSort(A, low, j); if(i < high) qSort(A, i, high);

}

43. Быстрая двоичная сортировка.

1.последовательно вставляем элементы исходно массива в БДП

2.выполняем симметричный обход сформированного дерева 3юпри посещении узлов – копируем содержимое в выходной массив O(log2n) – лучший O(n) – худший O(nlog2n) – вставок эл-тов

Минус – повышенные требования в объему памяти

44. Цифровая сортировка.

Цифровая поразрядная сортировка по принципу «сначала по младшей цифре»

Возьмем в нулевое множество все ключи с младшим битом 0, в множество с индексом 1, ключи с младшим битом 1 и т.д. Затем выполним подсчет ключей в множествах. Таким образом, получим С – массив счетчиков, в котором С [i] – это число ключей со старшей цифрой i. После подсчета ясно, что все ключи, имеющие младшую цифру 0, должны помещаться, начиная с нулевой позиции, ключи с цифрой 1 – начиная с позиции С [0], с цифрой 2 – с позиции С [0] + C [1] и т.д. Разместим ключи в соответствии с описанным правилом. Таким образом, добились разделения Ai<Ai+1. Далее повторим процесс по следующей цифре и т.д.

Рассмотрим на примере ключей в троичной системе счисления. Дано множество ключей:

102 211 012 020 201 111 121 022

Для троичной системы счисления размерность массива счетчиков будет три. Тогда С0 будет содержать 1 (имеется только один элемент, с 0 в старшем бите – 020), С1 будет содержать 4 (211, 201, 111, 121), и, наконец, С2 содержит 3 (102, 012, 022). Расставим теперь ключи в соответствии с номерами счетчиков 0, 1, 2. Получим

020 211 201 111 121 102 012 022.

Снова повторяем процесс расщепления по следующей цифре.

Последнее расщепление для последней цифры. С0 = 3 (012, 020, 022); С1 = 3 (102, 111,

121); С2 = 2 (201, 211).

Расставляем в соответствии с

Получена окончательная сортированная последовательность ключей.

Можно брать любую систему счисления. Удобно, если цифра – бит. Поэтому обычно используются либо 16-ричная (один бит – цифра), либо 256-ричная (один байт – цифра).

Алгоритм. Sort(A[1..n])

1.S<-1

2.For i=1 to key_size do

3.For j=o to 9 do

4.Queue9j0 <-ø

5.For k=1 to n do

6.BucketNumber<-(A[k], key/s)

7.Queue(BucketNumber)<-A[k]