сиаод / Otvety_Saod

58.Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.70

59.Стягивающие деревья. Нахождение стягивающего дерева методом поиска в глубину.71

76.Поиск с возвратом: алгоритм, применение метода к задаче нахождения

1. Алгоритмы.

Алгоритм – это заданная определенным образом последовательность действий, приводящая за конечное число шагов к достижению поставленной цели (к решению поставленной задачи).

Один и тот же алгоритм может быть записан несколькими способами. В практике программирования распространены:

•словесная запись на естественном языке;

•схемы алгоритмов, блок-диаграммы;

•решающие таблицы;

•алгоритмические языки (формальные языки).

Первый, второй и третий способы предназначены для человека, последний – для исполнителя-машины. Такая запись называется программой.

Существует три основных типов алгоритмов:

1.Последовательный алгоритм – такой, в котором действия выполняются в том порядке, в каком они написаны (в естественном порядке).

2.Условный алгоритм–конструкция ЕСЛИ – ТО – ИНАЧЕ. Запись в общем виде: ЕСЛИ условие ТО последовательность действий 1 ИНАЧЕ последовательность действий 2.

3.Циклическая конструкция. Называется она конструкцией WHILE - DO. Соответствующий алгоритм называется циклическим алгоритмом. Он задает многократное выполнение одних и тех же действий. Запись в общем виде: ПОКА условие ВЫПОЛНИТЬ последовательность действий. Последовательность может выполняться 0,1,... ,∞ раз.Этих трех конструкций (трех типов алгоритмов) достаточно для написания алгоритмов любой сложности

Салгоритмом связаны след. Моменты:

1)Каждый шаг алгоритма должен быть четко определен

2)Один и тот же алгоритм м.б. представлен разными способами

3)Для решения одной и той же задачи могут существовать несколько алгоритмов

4)В основу алгоритмов для решения одной и той же задачи м.б положены одинаковые принципы, влияющие на скорость решения

На практике существует 2 вида оценки эффективности:

1)Временная-является индикатором скорости работы алгоритма

2)Пространственная-показывает количество оперативной памяти, необходимой для работы алгоритмов

2.Вычислительная сложность алгоритмов и ее оценка.

Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности задачи.

Таким образом, будем различать временную T(n) и пространственную V(n) сложности алгоритма. При рассмотрении оценок сложности будем использовать только временную сложность. Пространственная сложность оценивается аналогично.

Самый простой способ оценки – экспериментальный, т. е. запрограммировать алгоритм и выполнить полученную программу на нескольких задачах, оценивая время выполнения программы. Однако этот способ имеет ряд недостатков. Во-первых, экспериментальное программирование – это, возможно, дорогостоящий процесс. Во-вторых, необходимо учитывать, что на время выполнения программ влияют следующие факторы:

1) временная сложность алгоритма программы;

2)качество скомпилированного кода исполняемой программы;

3)машинные инструкции, используемые для выполнения программы.

Часто, временная сложность алгоритма зависит от количества входных данных. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики.

Например, если число тактов (действий), необходимое для работы алгоритма, выражается как 11n2 + 19n·log n + 3n + 4, то это алгоритм, для которого T(n) имеет порядок O(n2). Фактически, из всех слагаемых оставляется только то, которое вносит наибольший вклад при больших n (в этом случае остальными слагаемыми можно пренебречь), и игнорируется коэффициент перед ним.

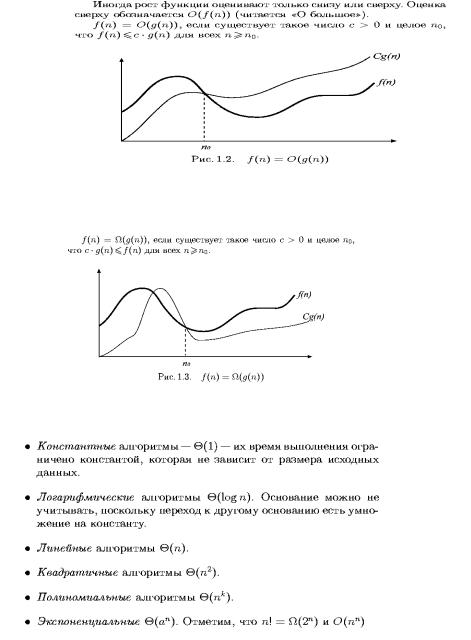
Когда используют обозначение O(), имеют в виду не точное время исполнения, а только его предел сверху, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n2), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов.

Оценка сверху

Оценка снизу

Классы сложности алгоритмов

3. Классификация структур.

1. По наличию явно заданных связей между элементами данных:

а) несвязные структуры: векторы, массивы, строки, стеки, очереди; б) связные структуры: связные списки

2.По признаку изменчивости структуры (т.е. изменения числа элементов и связей между ними:

а) статические; б) полустатические; в) динамические.

3.По характеру упорядоченности элементов структуры:

а) линейно-упорядоченные (линейные); б) нелинейные.

4. По характеру взаимного расположения элементов в памяти:

а) с последовательным распределением: векторы, массивы, строки, стеки, очереди; б) с произвольным связанным распределением: односвязные списки, двусвязные списки,

циклически связанные списки, ассоциативные списки.Для нелинейных структур – многосвязные списки, древовидные структуры и графовые структуры общего вида.

Структурой данных называется совокупность элементов данных между которых существует некоторые отношения. Причем элементами данных м.б. как простые данные, так и структура данных

S=(D,R) D-множество данных, R- отношения между ними

4. Стек. Абстрактный тип данных стек. Реализация стека с помощью массива.

Стек - линейный последовательный список, в котором доступ, включение и исключение элементов выполняется только с одного конца: k = n , т.е. доступен только последний элемент (вершина стека). Аббревиатура – "последний пришел – первым вышел". Вершина стека – это позиция, в которой находится последний поступивший элемент. Операции над элементами стека (включение и исключение) производятся с его вершины, причем в каждый момент для исключения доступен только верхний (последний) элемент . Вершина стека адресуется с помощью специального указателя. Стек считается пустым, если указатель смещен вниз на длину одной ячейки относительно низа стека. Возможные операции: 1)создать стек 2)поместить эл-т в стек 3)забрать эл-т 4)получить знач. верхнего элемента 5)проверить на пустоту 6)удалить. При работе со стеком необходимо учитывать, что если в процессе заполнения указатель выйдет за верхнюю границу, то происходит переполнение стека и новый элемент ввести уже невозможно. Для этого перед реализацией стека необходимо указывать его границы.

Представление стека – массивом, содержащим не меньшее число элементов, чем может быть заслано в стек. Для очередного элемента достаточно иметь один указатель t на этот элемент. Когда стек пуст, t = 0. Описание:

const ms = 100;

var stack : array[1..ms] of tt; t : integer;

Поместить новый элемент(Push(y)):

1)указатель перемещается "вверх" на длину слота или ячейки; 2)затем по значению указателя в стек помещается информация о новом элементе.

Чтобы добавить элемент в стек, нужно увеличить значение указателя на единицу, а затем занести в элемент массива с индексом t информацию из y:

t := t + 1; stack[t] := y;

Забрать элемент(Pop(y)):

1)прочитывается информация об исключаемом элементе по значению указателя; 2)затем указатель смещается "вниз" на один слот.

y := stack[t]; t := t - 1;

Получить знач. верхнего э-та(Top(y)): y:=stack[t]

Проверка на пустоту IsEmpty: if t = 0 then IsEmpty:=true

else IsEmpty:=false

При этом следует помнить, что t не может быть меньше 1 и больше MS. Следовательно, нужны проверки на пустоту и переполнение стека.

Извлекаем:

if t = 0 then write(ошибка)

else begin y := stack[t]; t := t - 1 end;

Добавляем:

if t = ms then write(ошибка)

else begin t := t + 1; stack[t] := y end;

Затраты постоянные О(1)-делается все за одну итерацию Недостаткипроверка на переполнение.

тек-структура данных, состоящая из упорядоченных элементов. Вставлять или удалять элементы можно только с одного конца, которая называется вершиной стека. Под упорядочиванием стека понимают, что существует элемент, который можно достать первым из стека

Last-In-First-Out(LIFO)

5.Стек. Абстрактный тип данных стек. Реализация стека с помощью указателей.

Стек - линейный последовательный список, в котором доступ, включение и исключение элементов выполняется только с одного конца: k = n , т.е. доступен только последний элемент (вершина стека). Аббревиатура – "последний пришел – первым вышел". Вершина стека – это позиция, в которой находится последний поступивший элемент. Операции над элементами стека (включение и исключение) производятся с его вершины, причем в каждый момент для исключения доступен только верхний (последний) элемент . Вершина стека адресуется с помощью специального указателя. Стек считается пустым, если указатель смещен вниз на длину одной ячейки относительно низа стека. Возможные операции: 1)создать стек 2)поместить эл-т в стек 3)забрать эл-т 4)получить знач. верхнего элемента 5)проверить на пустоту 6)удалить. Используется динамическое распределение памяти, т.е. выделять память для элемента списковой структуры в тот момент, когда этот элемент появляется во время выполнения программы, а не во время её компиляции. В

этом случае транслятор выделяет фиксированный объем памяти для хранения адресов динамически размещаемых элементов, а не самих элементов. Эти адреса называются указателями или ссылками.

Доступ к динамическим переменным осуществляется с помощью указателей (ссылок), которые становятся определенными после создания динамического элемента программы. Стек состоит из нескольких динамических областей памяти, причем указатель вышерасположенного элемента указывает на предыдущий элемент. Указатель стека должен указывать на верхний элемент стека. Для организации и ведения стека должны быть предусмотрены два указателя:

TYPE pStack = ^StackNode StackNode = record

info : integer

next : pStack- ук-ль на предыдущий end

var Stack : pStackуказатель на вершину Инициализация:

Stack:=nil

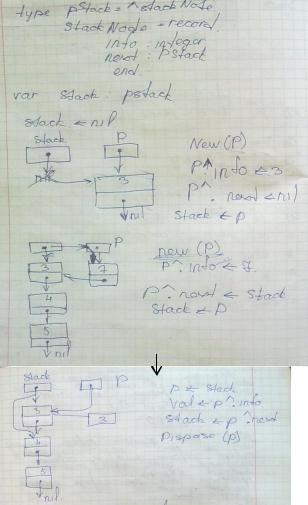
Поместить первый э-нт в стек:

1.выделить память под элемент; new(p);

2.занести в неё нужную информацию; p^.info := 5;

3.p^.next:=nil;

4.указателю stack присвоить значение указателя; stack := p;

Добавить эл-т в стек:

1.выделение памяти под новый э-нт; new(p); 2.заполнить информ. часть; p^.info:=7; 3.указатель на вешину стека; p^.next := stack; 4.stack := p

Удалить эл-т из стека:

1.считываем информацию эл-та; val := stack^.info 2.указываем рабочий указатель на вершину стека; p := stack 3.перемещаем стек к следующ. эл-ту; stack := p^.next 4.освождаем память; dispose(p)

Реализация стека с помощью указателей

6.Очередь. Абстрактный тип данных очередь. Реализация очереди с помощью массива.

Между собой объекты не переставляются Очередь-структура данных, упорядоченная таким образом, что элементы можно вставлять

только с одной стороны, а удалять с другой стороны, которая называется головой очереди(FIFO)

Элемент,который находится в голове очереди называется первым элементом Для абстрактного типа данных очередь определена следующими операциями:

1)Поместить элемент в очередь;

2)Забрать элемент из очереди

3)Получить значение первого элемента в очереди

4)Проверить является ли очередь пустой

Организация очереди с помощью массива Зададим массив и его размерность

type TypeElem=тип элемента очереди array Queue [1…MQ] of TypeElem integer F,B

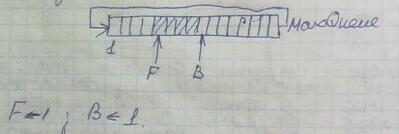
Алгоритм EnQueue(y)

1)Queue[B] <-y

2)If B=MQ then B<- 1

3)B<-B+1

Алгоритм DeQueue(y)

1)y<-Queue[F]

2)if F=MQ then F<-1

3)else F<-F+1

Алгоритм Front(y) 1) y<-Queue[F]

Алгоритм IsEmpty

1)F=B then return true(т.е.если очередь пустая)

2)else return false

Определение числа элементов в очереди: if r < f then k := mq + r – f else k := r – f.

Выч. затраты: const- O(1)

7. Очередь. Реализация очереди с помощью указателей.

Очередь – линейный последовательный список, в котором все включения производятся в конце списка (в хвосте очереди), а исключения – в начале (в голове очереди). Аббревиатура – "первым пришел – первым вышел". Для индикации хвоста и головы очереди организуются два указателя. f - указатель головного элемента очереди, r - адресует первый свободный слот, следующий за хвостовым.

При добавлении в очередь:

1)новый элемент заносится в слот, адресуемый указателем r;

2)после чего указатель необходимо передвинуть к следующему пустому слоту (вправо). При исключении из очереди:

1)извлекается элемент, адресуемый указателем f;

2)после чего f перемещается к следующему заполненному слоту. Для абстрактного типа данных имеются 6 операций:

1)создать пустую очередь, 2)поместить эл-т, 3)забрать эл-т, 4)получить знач. э-та стоящ. в начале очереди, 5)проверка на пустоту, 6)удалить очередь.

Естественно, что в процессе включения новых элементов в очередь, организованную таким образом рано или поздно наступит переполнение. Этого можно избежать, если после Amax переводить r на слот с адресом A1. Организованная таким образом очередь называется кольцевой. В такой очереди возможно любое из соотношений f < r, f = r, f > r. Основные операции над очередью – включение и исключение элемента.

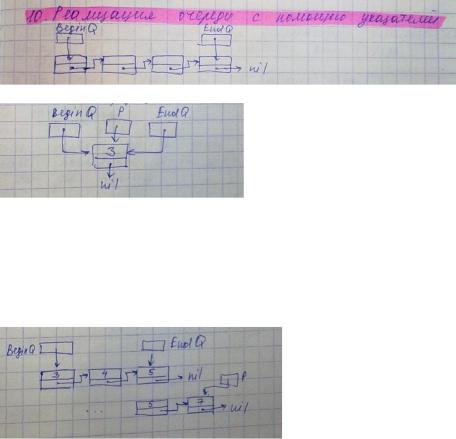
Характерная особенность списковых структур данных (связных списков, стеков, очередей и т.д.) – это способность изменять число элементов. Используется динамическое распределение памяти, т.е. выделять память для элемента списковой структуры в тот момент, когда этот элемент появляется во время выполнения программы, а не во время её компиляции. В этом случае транслятор выделяет фиксированный объем памяти для хранения адресов динамически размещаемых элементов, а не самих элементов. Эти адреса называются указателями или ссылками. Элементы, выделяемые динамически, не имеют имени, к ним нельзя обращаться стандартным путем. Доступ к динамическим переменным осуществляется с помощью указателей (ссылок), которые становятся определенными после создания динамического элемента программы. Нужны два указателя на начало и конец очереди, BeginQначало, EndQконец. Указатель последнего элемента очереди должен быть равен NIL. Таким образом, для работы с очередью нужны три переменных типа "указатель".

Тогда описание:

TYPE TP = ^SP;

SP = RECORD

INF : CHAR; LINK : TP END;

VAR F, K, R : TP; CH : CHAR;

занесение первого элемента в очередь:

new(p);

p^.info:=3;

p^.next:=nil;

BeginQ:=p;

EndQ:=p;

Добавление элемента:

new(p);

p^.info:=7;

p^.next:=nil;