
сиаод / Otvety_Saod
.pdf19.Не рекурсивный обход n-арного дерева.
Замена рекурсии циклом основана на использовании вспомогательного стека для хранения последовательности пройденных вершин от корня до текущей вершины
Не рекурсивный алгоритм обхода (стековый обход) дерева в прямом порядке:
Пусть T – указатель на бинарное дерево; А – стек, в который заносятся адреса еще не пройденных вершин; TOP – вершина стека; P – рабочая переменная.
1.Начальная установка: TOP:=0; P:=T.
2.Если P=nil, то перейти на 4. {конец ветви}
3.Вывести P^.info. Вершину заносим в стек: TOP:=TOP+1; A[TOP]:=P; шаг по левой ветви: P:=P^.llink; перейти на 2.
4.Если TOP=0, то КОНЕЦ.
5.Достаем вершину из стека: P:=A[TOP]; TOP:=TOP-1; Шаг по правой связи: P:=P^.rlink; перейти на 2.
20.Поиск в упорядоченных таблицах. Последовательный поиск в массиве.
Очень часто приходится решать следующую задачу: найти элемент с нужным значением ключа. Эту задачу приходится решать с использованием массивов, списков, деревьев. Эта задача решается по-разному в случае неупорядоченных или упорядоченных по возрастанию ключей элементов. В последнем случае можно не просматривать все элементы, а доходить только до элемента с ключом большим, чем требуемый.
Существует два альтернативных способа поиска: последовательный и двоичный. В последовательном списке может применяться только последовательный поиск в порядке следования указателей. В двоичном дереве естественным является двоичный поиск. В массиве может быть организован как тот, так и другой алгоритм.
Поставим задачу так: найти наименьший индекс (указатель) компоненты списка со значением ключа, равным Х.
Последовательный поиск в массиве
Пусть массив:
VAR A: ARRAY[1..N] OF INTEGER; X: INTEGER;
FUNCTION LOC(X: INTEGER): INTEGER; VAR I: INTEGER;
BEGIN
I := 0;
REPEAT I := I+ 1
UNTIL (A[I] = X) OR (I = N);
IF A[I] <> X THEN LOC := 0 ELSE LOC := I
END;
Процедура работает как для неупорядоченных, так и для упорядоченных массивов.
Неудобство функции в том, что проверка условия окончания сложная. Программу можно ускорить, если поставить "барьер", т.е. увеличить массив на один элемент и заслать туда значение искомого ключа. I := 0; A[N+1] := X;
REPEAT I := I + 1;
UNTIL A[ I ] = X;
IF I > N THEN LOC := 0 ELSE LOC := I;
Среднее число просмотров m = N / 2.
21.Поиск в упорядоченных таблицах. Двоичный поиск в массиве. Фибоначчиев поиск. Интерполяционный поиск.
Очень часто приходится решать следующую задачу: найти элемент с нужным значением ключа. Эту задачу приходится решать с использованием массивов, списков, деревьев. Эта задача решается по-разному в случае неупорядоченных или упорядоченных по возрастанию ключей элементов. В последнем случае можно не просматривать все элементы, а доходить только до элемента с ключом большим, чем требуемый.
Существует два альтернативных способа поиска: последовательный и двоичный. В последовательном списке может применяться только последовательный поиск в порядке следования указателей. В двоичном дереве естественным является двоичный поиск. В массиве может быть организован как тот, так и другой алгоритм.
Двоичный поиск:
Применяется для упорядоченных массивов. При двоичном поиске используется метод деления пополам. Поставим задачу так: найти наименьший индекс (указатель) компоненты списка со значением ключа, равным Х.
Алгоритм:
VAR A: ARRAY[1..N] OF INTEGER; X: INTEGER;
VAR I: INTEGER; BEGIN
I := 1; J := N; REPEAT
K := (I + J) DIV 2;
IF X > A[K] THEN I := K + 1 ELSE J := K - 1 UNTIL (A[K] = X) OR (I > J)
END.
Число просмотров m = log2N.
При N = 100: последовательный поиск выполнится за 50 просмотров (m = 50), двоичный за 6,62 (m = 6,62)

22. Поиск в линейном списке.
Как и в файле, поиск ведется строго последовательно. Он заканчивается либо когда элемент найден, либо когда достигнут конец списка.
Самое простое решение:
WHILE (P <> Nil) AND (P^.KEY <> X) DO P := P^.NEXT
Если элемента в списке нет, то при Р равном Nil нет следующего элемента P^.KEY. Поэтому надо ввести вторую часть проверки
WHILE P<> Nil DO
IF P^.KEY = X THEN { выход из цикла }
ELSE P := P^.NEXT;
Лучше воспользоваться логической переменной (флажком):
B := TRUE;
WHILE (P <> Nil) AND B DO
IF P^.KEY = X THEN B := FALSE ELSE P := P^.NEXT;
Элемент не найден, если P = Nil и B = TRUE.
23. Двоичное дерево поиска. Свойства. Основные операции.
Если для каждого узла ti дерева все ключи в левом поддереве меньше ключа ti, а все ключи в правом поддереве больше ключа ti, то это дерево упорядочено по ключам и называется деревом поиска. В дереве поиска можно найти место каждого ключа, двигаясь от корня и переходя на левое или правое поддерево каждого узла в зависимости от значения его ключа. Для поиска среди N элементов может потребоваться не более log2N сравнений, если дерево идеально сбалансировано.
В этом преимущество дерева перед линейным списком, в котором для поиска может потребоваться N сравнений. Поиск в упорядоченном двоичном дереве проводится по единственному пути от корня к искомому узлу (т.к. он проходит по единственному пути от корня к искомому узлу). Вып-ся те же операции как и с обычным деревом. Легче выпся оп-ии с поиском мин и макс ключа.
Основные операции: 1.Создать пустое БД 2.Включить узел в БД 3.Удалить узел из БД 4.Опр-ть пусто ли БД 5.Вып-ть поиск данных в БД
6.Обработать данные в узлах БД
7.Сохр-ть и восст-ть БД
8.Уничтожить БД.
Поиск Эл-та в 2-ном дереве:
Tree_Search(T,K).
1.i f (t=nil) or (k=T^.key) then return T
2.i f k<T^.key then return Tree_Search(T^.left,k)
3. else return Tree_Search(T^.right,k)
Iterative_Tree_Search(T,K).
1.while (T<>nil) and (k<>T^.key) do 2.if k<T^.key then TT^.left
3.else TT^.right; returnT.
Min and Max.
Мин. Ключ в дереве поиска можно найти по УК-лю left от корня, пока зн-е очередного УК-ля не станет = 0.
Tree_Minimum(T).
1.while T^.left<>nil do TT^.left 2.return T.
Для макс. Нужно заменить в алг-ме Tree_Minimum(T) left на right.
Добавление и удаление эл-та.
Эти операции сохр-ют сво-во упорядоченности. Добавление: алг-м вставляет нов. Эл-т в соответствии с бин. поиском.
Tree_Insert(T,z).
1.if T=nil then new(T)
2.T^.keyz T^.leftnil T^.rightnil 3.else if z<T^.key then Tree_Insert(T^.left,z) 4.else Tree_Insert(T^.right)
5.return T.
Затраты операций пропорциональны высоте дерева. Удаление: возможны 3 случая. 1.удаляемая вершина не имеет сыновей.
2.удаляемая вершина имеет 1-ого сына.

3.вершина имеет 2-х сыновей.
Delete(T,k).
1.if T<> nil then if k<T^.key then Delete(T^.left,k) 2.else if k>T^.key then Delete(T^.right,k)
3.else если узел не имеет сыновей:
4.if (T^left=nil) and (T^.right=nil) then q:=T;T:=nil; Dispose(q). 5.else если узел имеет сыновей:
6.else if (T^.left=nil) then q:=T; T:=T^.right; Dispose(q). 7.else (if T^.right=nil) then q:=T; T:=T^.left; Dispose(q).
8.else if (T^.left<> nil)and(T^.right<> nil) then q:=T; T:=T^.left; Dispose(q).
24. Добавление элемента в двоичном дереве поиска.
Алгоритм InsertTree (T, k) |
//k – добавляемое значение |
1.if T=nil
2.New (T)
3.T^.key←k
4.T^.left←nil
5.T^.right←nil
6.else
7.if (k<T^.key) then InsertTree (T^.left, k)
8.else InsrtTree (T^.right, k)
9.end if
10.end if
11.return T
Рассмотрим, например, вставку узла 8 в дерево BinSTree_1. Начав с корневого узла 25, определяем, что узел 8 должен быть в левом поддереве узла 25 (8<25). В узле 10 определяем, что место узла 8 должно быть в левом поддереве узла 10, которое в данный момент пусто. Узел 8 вставляется в дерево в качестве левого сына узла 10.
25. Удаление элемента в двоичном дереве поиска.
Удаление узла
Дано: дерево Т с корнем n и ключом K.
Задача: удалить из дерева Т узел с ключом K (если такой есть). Алгоритм:
Если дерево T пусто, остановиться
Иначе сравнить K с ключом X корневого узла n.
o Если K>X, рекурсивно удалить K из правого поддерева Т. o Если K<X, рекурсивно удалить K из левого поддерева Т.
oЕсли K=X, то необходимо рассмотреть два случая.
Если одного из детей нет, то значения полей второго ребёнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом m.
Если оба потомка присутствуют, то
найдём узел m, являющийся самым левым узлом правого поддерева;
скопируем значения полей (ключ, значение) узла m в соответствующие поля узла n.
у предка узла m заменим ссылку на узел m ссылкой на правого потомка узла m (который, в принципе, может быть равен ПУСТО).
освободим память, занимаемую узлом m (на него теперь никто не указывает, а его данные были перенесены в узел n).
Алгоритм Delete (T, k)
1.if T≠nil then
2.if k<T^.key then Delete (T^.left, k)
3.else if k>T^.key then Delete (T^.right, k)
4.else
5.if (T^.left=nil) and (T^.right=nil) then
6. p←T, T←nil, Dispose (p)
7.else if (T^.left=nil) then
8. p←T, T←T^.right, Dispose (p)
9.else if (T^.right=nil) then
10. p←T, T←T^.left, Dispose (p)
11.else Del (T^.right, p)
Del (T, p)
1.if T^.left=nil then
2.p^.key←T^.key
3.p1←T
4.T←T^.right
5.Dispose (p1)
6.return
7.else
8.Del (T^.left, p)
Вычислительная сложность.
Средний вариант – O(log n), худший случай – O(n).
26. Абстрактная таблица. Основные операции. Способ реализации.
Таблица – одна из важнейших структур данных, применяемая для хранения. Таблица состоит из совокупности элементов, снабженных отличительными признаками, называемыми ключами.
Одна строчка в таблице называется записью. Каждая колонка таблицы называется полем. Одно или несколько полей играют особую роль и используются при поиске элементов. Их
называют ключами записи. Ключи используются для доступа к элементам таблицы. Таблицы данных классифицируются по различным признакам:
1.По месту хранения
a.В оперативной памяти
b.Во внешней памяти
2.По отношению связей между элементами
a.Линейная
b.Нелинейная
3.По упорядоченности элементов
a.Упорядоченные
b.Неупорядоченные
Операции:
1.Включить в таблицу новый элемент.
2.Удалить из таблицы элемент, поисковый ключ которого совпадает с заданным элементом.
3.Извлечь из таблицы элемент, поисковый ключ которого совпадает с заданным элементом.
4.Обойти элементы таблицы в порядке следования их поисковых ключей.

5.Определить, пуста ли таблица.
6.Определить количество элементов в таблице. Организации таблицы делятся на линейные и нелинейные. Способ реализации:
1.Линейный
a.Неупорядоченный массив
b.Неупорядоченный связный список
c.Упорядоченный массив
d.Упорядоченный связный список
2.Нелинейный
a.Бинарное дерево поиска
b.Сбалансированное дерево поиска
c.Хеш-таблица
d.Б-дерево
27.AVL-деревья. Свойства. Вращение. Теорема высоты.
Для каждого узла высота его поддеревьев различается не более чем на 1. Все операции аналогины операциям над БДП за исключением вставки и удаления узла, т.к.необходимо сохранение сбалансированности. Для хранения инфы о сбалансированности вводят дополнительное поле (Balance), указывающее какое поддерево длиннее( leftheavy, rightheavy, balanced).
TBalance=( leftheavy, rightheavy, balanced); TAVLTree=^AVLNode;
AVLNode=record
Key:integer;
Left, right: TAVLTree; Balance:TBalance; End;
Адельсон-Вельский-Ландис
AVL-дерево с n ключами имеет высоту H = O(logN)
Дерево поиска называется АВЛ – деревом, если для каждой его вершины высоты левого и правого поддеревьев отличаются не более чем на 1.
АВЛ - дерево
Высота AVL-деревьев оценивается сверху логарифмически в зависимости от числа вершин: h <= C log2 n . Высота лежит в диапазоне от log2(n + 1) до 1.44 log2(n + 2)
Повороты при балансировке
Пусть r – корень АВЛ-дерева, у которого имеется левое поддерево (ТL) и правое поддерево (TR). Если добавление новой вершины в левое поддерево приведет к увеличению его высоты на 1, то возможны три случая:
1)если hL = hR, то ТL и TR станут разной высоты, но баланс не будет нарушен;
2)если hL < hR, то ТL и TR станут равной высоты, т. е. баланс даже улучшится;

3)если hL > hR, то баланс нарушиться и дерево необходимо перестраивать.
Введём в каждую вершину дополнительный параметр Balance (показатель баланса), принимающий следующие значения: -1, если левое поддерево на единицу выше правого;0, если высоты обоих поддеревьев одинаковы;1, если правое поддерево на единицу выше левого.
Если в какой-либо вершине баланс высот нарушается, то необходимо так перестроить имеющееся дерево, чтобы восстановить баланс в каждой вершине. Для восстановления баланса будем использовать процедуры поворотов АВЛ-дерева.
1 |
LL - поворот |
|
|
|
|
|
|
p |
|
|
p |
|
|
|
|
-1 |
-2 |
A |
0 |
|
|
B |
|
|
|||
q |
|
|
|
|
||
L |
|
|
|
|
|
|
|
A 0 -1 |
|
LL |
|
B |
0 |
|
|
|
|
|||
|
L |
|
=> |
|
|
|
|
|
|
|
|
|
|
|
|
T3 |
|
|
|
|
|
|
|
|
T1 |
|
|
T1
q := p→Left q→Balance := 0 p→Balance := 0 p→Left := q→Right q→Right := p
p := q
2 |
LR – поворот |
|
L
q
A
0 +
1
R
r
B
T1 T2
T2 |
T2 |
T3 |
Алгоритм на псевдокоде
LL - поворот
p |
|
|
|
|
|
p |
|
C - |
- |
|
|
|
B |
0 |
|
LR |
|
|
|
|
|||
1 |
2 |
|
|
|
|
|
|
|
|
=> |
A |
0 |
|
C |
+ |
|
|
|
|
10 |
|||
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
-
01
+
1 |
T4 |
|
|
|
|
|
T2 |
T3 |
T3 |
T1 |
T4 |
 LR – поворот
LR – поворот
Алгоритм на псевдокоде

LR - поворот
q := p→Left, r := q→Right
IF (r→Balance<0) p→Balance := +1 ELSE p→Balance := 0 FI IF (r→Balance>0) q→Balance := –1 ELSE q→Balance := 0 FI r→Balance := 0
p→Left := r→Right, q→Right := r→Left r→Left := q, r→Right := p, p := r
3 |
RR – поворот |
|
|
|
|
q |
|
|
|
|
|
|
|
|
p |
|
|
|
RR |
|
|
+ |
+ |
|
|
=> |
B 0 |
|
|
|
|
|||
|
A 1 |
2 |
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
0 |
q |
|
A 0 |
|
|
|
|
|
||
|
|
B |
1+R |
|
|
|
T3
T1
T2 |
T3 |
T1 |
T2 |
|
|
RR – поворот
Алгоритм на псевдокоде
RR - поворот
q := p→Right q→Balance := 0 p→Balance := 0 p→ Right:= q→ Left q→ Left := p
p := q
4 |
RL – поворот |
|
 p
p
A |
+ |
|
|
q |
|
1 |
|
|
|
||
|
+ |
|
|
|
|
|
2 |
R |
|
|
|
|
|
|
C |
0 |
|
|
|
|
- |
RL |
|
|
|
L |
|
||
|
|
|
|
||
|
|
|
1 |
=> |
|
|
|
|
|
||
- |
|
|
r |
|
|
B |
|
|
|
||
1 |
|
|
|
||
0 + |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
p |
|
|
|
B |
0 |
|
|
A |
|
C |
+ |
|
0 |
10 |
|||
|
|
|||
|
- |
|
|
|
|
1 |
|
|
T1
|
|
T2 |
T3 |
|
T4 |
T1 |
T4 |
T2 |
T3 |
|
|
|
RL – поворот |
|
|
|
Алгоритм на псевдокоде |
|
|
|
RL - поворот |
|
|
q := p→ Right, r := q→ Left
IF (r→Balance>0) p→Balance := -1 ELSE p→Balance := 0 FI IF (r→Balance<0) q→Balance := 1 ELSE q→Balance := 0 FI r→Balance := 0
p→ Right:= r→ Left, q→ Left:= r→ Right r→ Left := p, r→Right := q, p := r
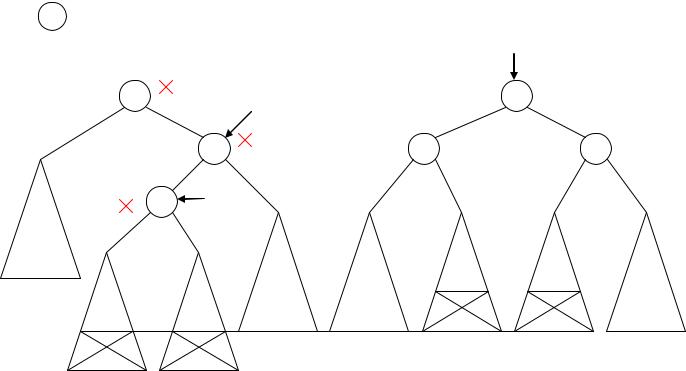
28. Добавление вершины в AVL-дерево.
Добавление новой вершины в АВЛ-дерево происходит следующим образом. Вначале добавим новую вершину в дерево так же как в случайное дерево поиска (проход по пути поиска до нужного места). Затем, двигаясь назад по пути поиска от новой вершины к корню дерева, будем искать вершину, в которой нарушился баланс (т. е. высоты левого и правого поддеревьев стали отличаться более чем на 1). Если такая вершина найдена, то изменим структуру дерева для восстановления баланса с помощью процедур поворотов.
Алгоритм на псевдокоде
Добавление в АВЛ – дерево (D: данные; Var p: pVertex);
Обозначим Рост – логическая переменная, которая показывает выросло дерево или нет.
IF (p = NIL)
new(p), p→Data := D, p→Left := NIL, p→Right := NIL p→Balance := 0, Рост := ИСТИНА
ELSE
IF (p→Data > D)
Добавление в АВЛ – дерево (D, p→Left)
IF (Рост = ИСТИНА) {выросла левая ветвь}
IF (p→Balance > 0) p→Balance := 0, Рост := ЛОЖЬ
